LSTM+CNN模型厄尔尼诺事件预测

Background

一、什么是ENSO现象

ENSO（El Niño-Southern Oscillation）是发生于赤道东太平洋地区的风场和海面温度震荡。ENSO是低纬度的海-气相互作用现象，在海洋方面表现为厄尔尼诺-拉尼娜的转变，在大气方面表现为南方涛动。

二、ENSO现象有什么影响

包括厄尔尼诺现象及拉尼娜现象在内的厄尔尼诺-南方涛动现象会造成全球性的气温及降水变化。例如当厄尔尼诺现象发生时，南美洲地区会出现暴雨，而东南亚、澳大利亚则出现干旱。依赖农业和渔业的国家，特别是太平洋附近的发展中国家，通常受影响最大。

三、数据集介绍

Nino3.4指数定义为Nino3.4区（170°W-120°W，5°S-5°N）区域平均海温距平，气候平均值是1981-2010年。可以在美国国家海洋大气管理局网站（https://psl.noaa.gov/data/timeseries/monthly/NINO34/）下载。

MEI.v2指数利用海平面气压、海表温度、地面风的纬向分量、地面风的经向分量、热带太平洋海盆（30°S-30°N和100°E-70°W）上空的长波辐射五个变量计算得到。可在美国国家海洋大气管理局网站（https://psl.noaa.gov/enso/mei/）下载。

---

基于LSTM+CNN的时间序列预测

Nino指数能够在一定程度上反映厄尔尼诺或者拉尼娜现象，数据表现为一段时间序列。

针对该时间序列数据，我们可以对未来短期的Nino指数变化进行推测。时间序列处理算法按照算法类型大致可分为经典算法、深度学习算法、机器学习算法、启发式算法，按照数据维度可分为频域处理方法、时域处理方法。在本案例中，Nino指数是已经被处理好的数据，且由于数据量较少，经典算法和机器学习算法可能无法给出理想的解决办法。

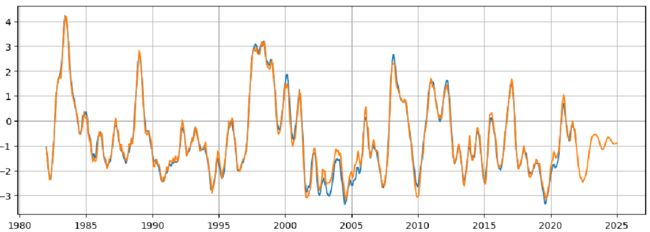
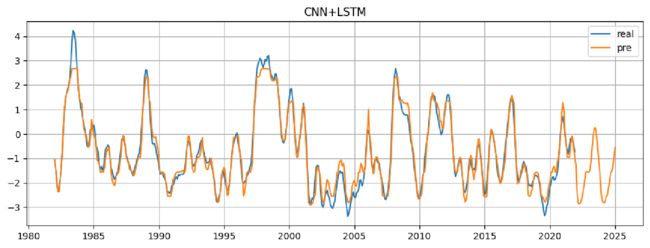
在数据探索性分析(EDA)和特征工程(FE)之后，我们采用一维卷积神经网络对其进行预测。在设定一个窗口大小后，采用滑动窗口的思想，对原始数据的信息进行学习，得到的结果如下:

CNN虽然在原始数据集上有着不错的表现，但是在未来数据的预测中，效果却不是那么好。这是由于CNN注重局部特征，而在未来数据的推测中，$f[n]=CNN(f[n-ws-1:n-1])$，数据会倾向于收敛或是震荡。

为了解决模型无法从过往的信息中学习经验的问题，我们引入了LSTM长短期记忆模型，以期过往的经验模式能够为我们的预测提供决策。

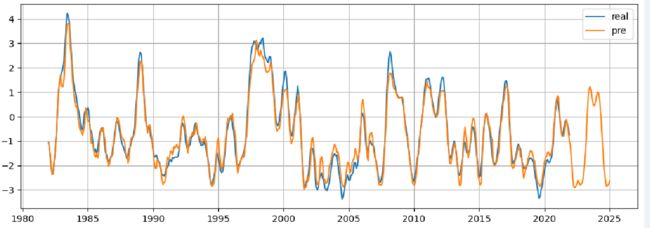
基于LSTM模型得到的预测结果如下图所示：

相较于CNN模型，该模型的均方根误差(MSE)较高，拟合效果不如原始CNN，但它在未来趋势上的映射要优于CNN。可以发现，未来三年的特征模式与2010-2012年的模式类似。

既然CNN注重局部信息，LSTM又能保存长期信息，那如果采用CNN+LSTM的方式能不能有一些新的进展呢？

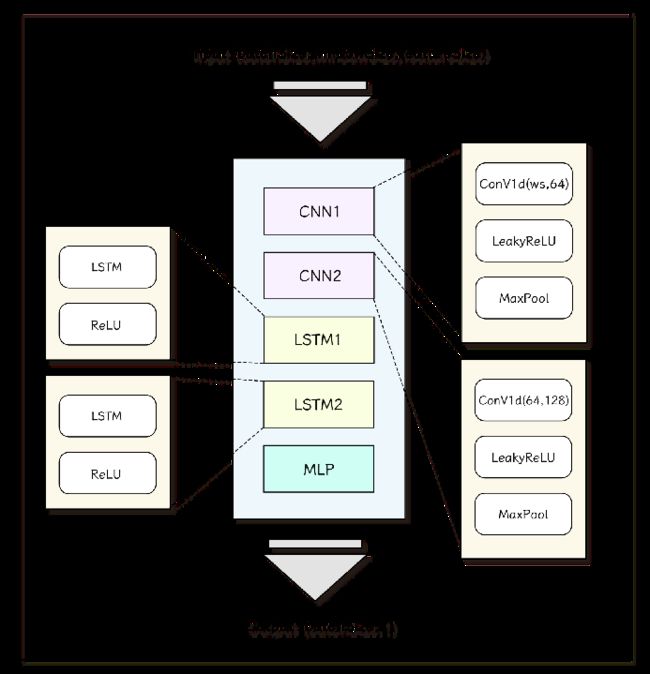
基于这个思想，我们采用了下图的模型作为预测模型。

两层CNN用于学习局部特征，两层LSTM用于学习长时间特征。

在激活函数方面，我们注意到原始数据有大量的负值，因而采用了对负值比较友好的LeakyReLu激活函数。

每层卷积之后，添加一个池化层，以期达到减少参数量和增强模型泛化能力(非线性能力)的作用。

最后一层通过多层感知机(MLP)对数据维度进行映射，得到我们的输出结果。

我们发现，该模型在前期的拟合上精度不是那么高，通过测试发现这是由于LeakReLu激活函数引起的现象。但是该模型在后半段已经有着可以接受的精度了。

由于模型比较简单，且训练样本较少，总所周知数据决定了模型的上限，为了解决这个问题，我们可以采用上采样的方式处理原始数据，以期得到更多的数据集。

诶，但是我们就是没有做，因为上采样也是基于该数据的，在误差将会被扩大。

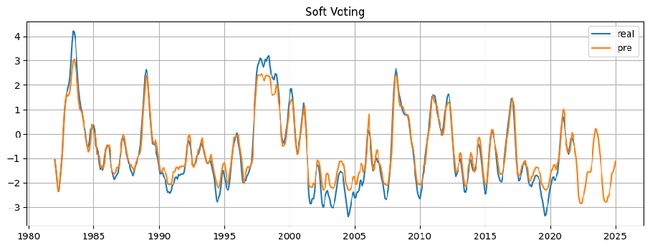
于是我们采用了一种比较偷懒的方法，软投票Soft Voting来对单模进行集成，以期获得更好的学习效果和泛化能力。

我们通过三个模型(CNN、CNN+LSTM(LeakyReLu,三层CNN)、CNN+LSTM(用池化代替CNN的LeakyReLU,两层CNN)进行学习，根据损失误差分别赋予各自权重，最后的结果由三个模型投票得到。

可以发现，在未来，23年~24年有可能会发生拉尼娜现象。

---

代码实现

1️⃣数据预处理阶段

首先是导入我们的模块，这部分不做过多的赘述~

import torch
import pandas as pd
import numpy as np
import torch.nn as nn
import torch.nn.functional as F
import matplotlib.pyplot as plt

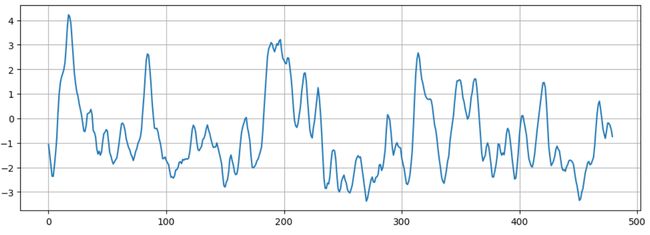
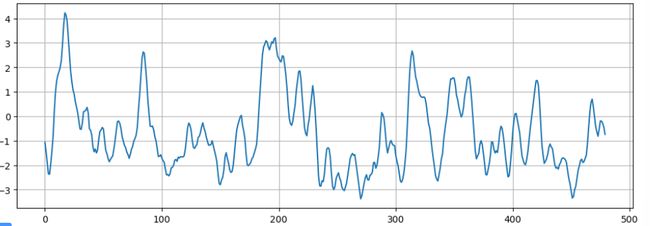
EDA阶段，读取数据并展示，我们选取了1982~2021年共四十年的数据。

data=pd.read_excel(r"data1.xlsx")
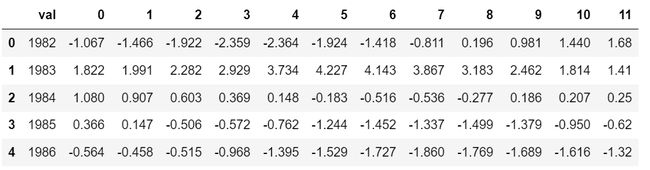
data.head()

数据的维度是13*40，第一列并不是我们所需要的。

为了方便处理，可以通过np.ravel()函数对数据进行展平。

data=np.array(data.drop("val",axis=1).values).ravel()
plt.figure(figsize=(12,4))
plt.grid(True)
plt.plot(data)
plt.show()

我们将数据划分为训练集和测试集:

# 划分数据集
test_size=12
train_set=data[:-test_size]
test_set=data[-test_size:]

在下一步的操作中，我们将会对数据进行归一化处理(其实也没有必要啦，因为只有单维度的数据，量纲影响不是那么关键)

from sklearn.preprocessing import MinMaxScaler
# 归一化处理
scaler = MinMaxScaler(feature_range=(-1, 1))
train_norm = scaler.fit_transform(train_set.reshape(-1, 1))

为了能够输入模型，需要构造一个可迭代的数据集！这里可以选择继承DataLoader类，或者自己设定一个数据迭代器！

# 转换成 tensor
train_norm = torch.FloatTensor(train_norm).view(-1)
window_size = 12

def input_data(seq,ws):
    out = []
    L = len(seq)
    for i in range(L-ws):
        window = seq[i:i+ws]
        label = seq[i+ws]
        out.append((window, label))
    return out
train_data = input_data(train_norm,window_size)
# 打印一组数据集
train_data[0]

window_size表示了滑动窗口的大小。我们将滑动窗口内的数据作为x，输出结果作为$\hat{y}$，与真实的y进行比较。

(tensor([-0.3926, -0.4976, -0.6175, -0.7325, -0.7338, -0.6180, -0.4849, -0.3253,
         -0.0604,  0.1461,  0.2669,  0.3300]),
 tensor(0.3674))

总结一下，在EDA阶段，我们做了：

✅ 数据格式处理，筛选出需要的数据

✅ 对数据分布进行探查

✅ 数据归一化

✅ 划分训练集

✅ 构建数据生成器

---

2️⃣模型准备

在这阶段中，我们采用软投票的方式对多个模型的结果进行修正，具体内容可以见上文。

那我们先介绍模型一！正宗CNN！

class CNN_Net2(nn.Module):
    def __init__(self):
        super(CNN_Net2, self).__init__()
        self.hidden=nn.Sequential(
            nn.Conv1d(12,64,1),
            nn.AdaptiveAvgPool1d(output_size=32),
            nn.Conv1d(64,128,1),
            nn.AdaptiveAvgPool1d(output_size=32),

            nn.Flatten(),
            nn.Linear(128*32,512),
            nn.ReLU(),
            nn.Linear(512,256),
            nn.ReLU(),
            nn.Linear(256,1)
        )
        
    def forward(self,x):
        N, T = x.shape[0], x.shape[1]
        x = x.transpose(1, 2)  
        return self.hidden(x)

一如既往的简洁明快，一维卷积也就是nn.Conv1d要求的输入格式为：[bs,f,n]，f为特征维度。而输入nn.Linear()的数据则要求是一维的，因此需要将其展平。

至于x为什么要做个transpose交换第二和第三维度，是因为我们输入的数据格式为[bs,1,ws]，这在后面会提到，这里按下不表。

下面是我们的模型二，CNN+LSTM模型。

class CNN(nn.Module):
    def __init__(self, output_dim=1):
        super(CNN, self).__init__()
        self.relu = nn.ReLU(inplace=True)
        self.conv1 = nn.Conv1d(12, 64, 1)
        self.lr=nn.LeakyReLU(inplace=True)
        self.maxpool1 = nn.AdaptiveAvgPool1d(output_size=32)
        self.conv2 = nn.Conv1d(64, 128, 1)
        self.maxpool2 = nn.AdaptiveAvgPool1d(output_size=32)

        self.flatten = nn.Flatten()
        self.lstm1 = nn.LSTM(128 * 32, 1024)
        self.lstm2 = nn.LSTM(1024, 256)
        self.fc = nn.Linear(256, 128)
        self.fc1 = nn.Linear(128, 64)
        self.fc2 = nn.Linear(64, 32)
        self.fc3 = nn.Linear(32, output_dim)

    def forward(self, x):
       
        N, T = x.shape[0], x.shape[1]
        x = x.transpose(1, 2)  

        x = self.conv1(x)  # torch.Size([1, 64, 1])
        x=self.lr(x)
        x = self.maxpool1(x)  # torch.Size([1, 64, 32])
        x = self.conv2(x)  # torch.Size([1, 128, 32])
        x=self.lr(x)
        x = self.maxpool2(x)  # torch.Size([1, 128, 32])
        # x = self.conv3(x)  # torch.Size([32, 300, 298])
        # x = self.maxpool3(x)  # torch.Size([32, 300, 100])
        x = self.flatten(x)
        # 注意Flatten层后输出为(N×T,C_new)，需要转换成(N,T,C_new)
        _, C_new = x.shape
        x = x.view(N, T, C_new)

        # LSTM部分
        x, h = self.lstm1(x)
        x, h = self.lstm2(x)
        # 注意这里只使用隐层的输出
        x, _ = h
  
        x = self.fc(x.reshape(-1,))
        x = self.relu(x)
        x = self.fc1(x)
        x = self.relu(x)
        x = self.fc2(x)
        x = self.relu(x)
        x = self.fc3(x)

        return x

池化的操作会让第三维度有所变化，而输入LSTM的模型的数据维度应该是[bs,F,T]，其中F表示初始序列长度，T表示特征变化，在这里，经过卷积和池化后的数据维度为：[1,128,32]，经过Flatten()操作后，数据的维度变成[bs,F*T]也就是[1,1*128*32],我们还需要将其转化为LSTM模型接受的维度。注意CNN和LSTM接收维度一个是dim=1一个是dim=2。

对于LSTM，在Pytorch中，有如下的输出关系：
$$y,h=LSTM(x)$$
我们需要的最终结果是h里的第一个维度，但每次传递的依旧是y（实际上h[0]==y)。

---

3️⃣网络训练阶段

在本阶段，我们需要设置的有：

• 设备(GPU)
• 损失函数
• 优化器
• 模型存储路径
• 训练参数
  • 精度
  • 误差值
  • 迭代次数等

import time
device="cuda" if torch.cuda.is_available() else "cpu"
torch.manual_seed(101)
model =CNN()
model=model.to(device)
Mloss=100000
path="./best_model.pth"
# 设置损失函数,这里使用的是均方误差损失
criterion = nn.MSELoss()
# 设置优化函数和学习率lr
optimizer = torch.optim.Adam(model.parameters(), lr=0.001) 
# 设置训练周期
epochs = 100
criterion=criterion.to(device)
model.train()
start_time = time.time()
total_loss=0

检查你的cuda是否可用，如果可用，将损失函数和模型全部搬到cuda上处理。

for epoch in range(epochs):
    for seq, y_train in train_data:
        # 每次更新参数前都梯度归零和初始化
        seq,y_train=seq.to(device),y_train.to(device)
        optimizer.zero_grad()
        # 注意这里要对样本进行reshape，
        # 转换成conv1d的input size（batch size, channel, series length）
        y_pred = model(seq.reshape(1,1,-1))
        loss = criterion(y_pred, y_train)
        loss.backward()
        optimizer.step()
        total_loss+=loss
    if total_loss.tolist()<Mloss:
        Mloss=total_loss.tolist()
        torch.save(model.state_dict(),path)
        Model_Loss[0]=total_loss.tolist()
        print("Saving")
    total_loss=0
    
    print(f'Epoch: {epoch+1:2} Loss: {loss.item():10.8f}')  
print(f'\nDuration: {time.time() - start_time:.0f} seconds')

可以注意到，我们在每次训练的时候，都会从一个迭代器中读取数据，这个迭代器可以是继承自DataLoader的，也可以是自己设定的。将数据搬到device上后，我们就需要按照以下模板训练网络：

1️⃣ 优化器梯度归零

2️⃣ 利用模型对bx进行训练，得到pred

3️⃣ 通过损失函数计算loss(pred,by)

4️⃣ 损失函数反向更新梯度

5️⃣ 更新优化器

6️⃣ 记录误差与精度，并在设定好的规则下存储最优模型参数

我们可以将这个阶段封装

def Train(model,seed=1):
    device="cuda" if torch.cuda.is_available() else "cpu"
    model=model.to(device)
    Mloss=100000
    path="./best_model%d.pth"%seed
    # 设置损失函数,这里使用的是均方误差损失
    criterion = nn.MSELoss()
    # 设置优化函数和学习率lr
    optimizer = torch.optim.Adam(model.parameters(), lr=0.001) 
    # 设置训练周期
    epochs = 100
    criterion=criterion.to(device)
    model.train()
    start_time = time.time()
    total_loss=0
    for epoch in range(epochs):
        for seq, y_train in train_data:
            # 每次更新参数前都梯度归零和初始化
            seq,y_train=seq.to(device),y_train.to(device)
            optimizer.zero_grad()
            # 注意这里要对样本进行reshape，
            # 转换成conv1d的input size（batch size, channel, series length）
            y_pred = model(seq.reshape(1,1,-1))
            loss = criterion(y_pred, y_train)
            loss.backward()
            optimizer.step()
            total_loss+=loss
        if total_loss.tolist()<Mloss:
            Mloss=total_loss.tolist()
            torch.save(model.state_dict(),path)
            Model_Loss[seed]=total_loss.tolist()
            print("Saving")
        total_loss=0
        print(f'Epoch: {epoch+1:2} Loss: {loss.item():10.8f}')  
    print(f'\nDuration: {time.time() - start_time:.0f} seconds')
    return model

这样，方便我们对每个模型进行训练了。

m2=CNN_Net2()
m2=Train(m2,2)

m1=CNN_Net1()
m1=Train(m1,1)

m0=CNN()
m0=Train(m0,0)

---

4️⃣结果展示阶段

这个阶段要做的事情，就是让模型调成eval()模式，并且在冻结梯度更新的情况下，对数据进行预测。

我们的工作有：

• 加载最优结果模型
• 根据现有数据计算得到预测曲线
• 根据预测曲线预测未来三年的结果
• 拼接数据并展示
• 对每个数据利用多个模型进行决策

值得注意的是，我们之前做了归一化，最后的结果要返回去。需要借助scaler.inverse_transform函数。

然后我们可以通过np.arange()生成时间序列，作为坐标轴。

def Show(model,title="CNN+LSTM"):
    model.eval()
    model=model.cpu()
    model.state_dict=torch.load(path)
    preds=train_norm
    PreV=[]
    for i in range(480):
        seq=torch.FloatTensor(preds[i:i+window_size]).reshape(1,1,-1)
        with torch.no_grad():
            try:
                v=model(seq).item()
            except:
                break
            PreV.append(v)
            
    # 预测未来36个月
    preds=PreV[-window_size:]
    future=36
    for i in range(future):
        seq=torch.FloatTensor(preds[i:i+window_size]).reshape(1,1,-1)
        with torch.no_grad():
            preds.append(model(seq).item())
            
    PreV=train_norm[:window_size ].tolist()+PreV+preds[window_size:]
    true_predictions = scaler.inverse_transform(np.array(PreV).reshape(-1, 1))
    print(true_predictions.shape)
    
        # 对比真实值和预测值
    plt.figure(figsize=(12,4))
    plt.grid(True)
    x1=np.arange('1982-01-01', '2022-01-01', dtype='datetime64[M]').astype('datetime64[D]')
    plt.plot(x1,data,label='real')
    x2 = np.arange('1982-01-01', '2025-02-01', dtype='datetime64[M]').astype('datetime64[D]').reshape(-1,1)
    plt.plot(x2,true_predictions,label="pre")
    plt.legend()
    plt.title(title)
    plt.show()

在软投票方面，我们只需要做以下修改：

preds=train_norm
PreV=[]
for i in range(480):
    seq=torch.FloatTensor(preds[i:i+window_size]).reshape(1,1,-1)
    with torch.no_grad():
        try:
            v=0
            for i,m in enumerate(model_list):
                v+=m(seq).item()*Model_Loss[i]
        except:
            break
        PreV.append(v)

Model_Loss是三个模型的权重，算法为计算各自占比的逆事件的占比，简单作为权重放上去了。

# 预测未来36个月
preds=PreV[-window_size:]
future=36
for i in range(future):
    seq=torch.FloatTensor(preds[i:i+window_size]).reshape(1,1,-1)
    with torch.no_grad():
        v=0
        for i,m in enumerate(model_list):
             v+=m(seq).item()*Model_Loss[i]
        preds.append(v)
            
PreV=train_norm[:window_size ].tolist()+PreV+preds[window_size:]
true_predictions = scaler.inverse_transform(np.array(PreV).reshape(-1, 1))