【西瓜书】第4章决策树---学习笔记
1.基本流程
createBranch()函数的伪代码:
检测数据集中的每个子项是否属于同一分类:
If so return 类标签;
Else
寻找划分数据集的最好特征
划分数据集
创建分支节点
for 每个划分的子集
调用函数createBranch并增加返回结果到分支节点中
return 分支节点
2.划分选择
2.1信息增益
假 定 当 前 样 本 集 合 D D D 中 第 k k k 类 样 本 所 占 的 比 例 为 P k ( k = 1 , 2 , . . . , ∣ y ∣ ) P_ k (k = 1, 2,. . . , |y| ) Pk(k=1,2,...,∣y∣)
信息熵定义: E N T ( D ) = − Σ k = 1 ∣ y ∣ p k l o g 2 p k ENT(D) = -\Sigma^{|y|}_{k=1}p_klog_2p_k ENT(D)=−Σk=1∣y∣pklog2pk
计算信息熵的示例代码:
def Entropy(dataSet):
num = len(dataSet)
labelCounts = {}
for featVec in dataSet: # 统计每个类别的数量
currentLabel = featVec[-1] #最后1列为键
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0 #初始值=0
labelCounts[currentLabel] += 1 #统计+1
entropy = 0.0
for key in labelCounts: #
prob = float(labelCounts[key])/num
entropy -= prob * math.log(prob,2) #log base 2
return entropy
创建数据集
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
featureNames = ['no surfacing','flippers'] #不浮出水面是否存活 ,有无脚蹼
#change to discrete values
return dataSet, featureNames
测试一下
myData,myFeatureNames = createDataSet()
print "the old dataset:\n",myData
myEntropy = Entropy(myData)
print "my test entropy should be 0.97095 :\n",myEntrop
2.2增益率
定义: G a i n r a t i o ( D , a ) = G a i n ( D , a ) I V ( a ) Gain ratio(D,a) = \frac{Gain(D,a)}{IV(a)} Gainratio(D,a)=IV(a)Gain(D,a)
其中 I V ( a ) = − Σ v = 1 V ∣ D v ∣ ∣ D ∣ l o g 2 ∣ D v ∣ ∣ D ∣ IV(a) = - \Sigma^V_{v = 1}\frac{|D^v|}{|D|}log_2\frac{|D^v|}{|D|} IV(a)=−Σv=1V∣D∣∣Dv∣log2∣D∣∣Dv∣
称为属性a的“固有值”,属性a可能取值数目越多,则 I V ( a ) IV(a) IV(a)越大
2.3基尼指数
定义: G i n i i n d e x ( D , a ) = Σ v = 1 V ∣ D v ∣ ∣ D ∣ G i n i ( D v ) Gini index(D,a) = \Sigma^V_{v= 1}\frac{|D^v|}{|D|}Gini(D^v) Giniindex(D,a)=Σv=1V∣D∣∣Dv∣Gini(Dv)
其中 G i n i ( D ) = 1 − Σ k = 1 ∣ y ∣ p k 2 Gini(D) = 1 - \Sigma^{|y|}_{k=1}{p^2_k} Gini(D)=1−Σk=1∣y∣pk2
3.剪枝
3.1预剪枝
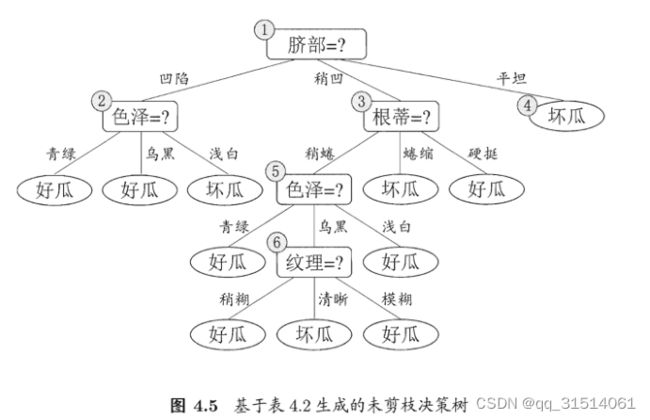
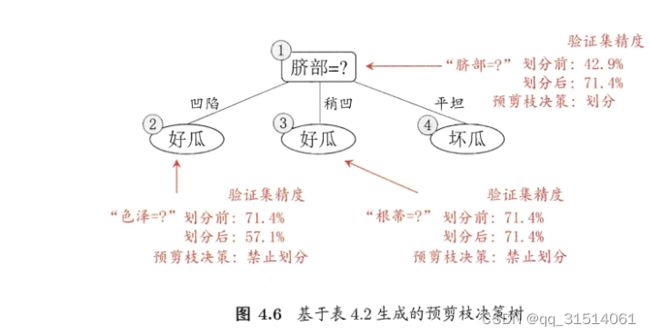
优点:预剪枝使得决策树的很多分支都没有 " 展开,这不仅降低了过拟合的风险,还显著减少了决策树的训练时间开 销 .
缺点:有些分支的当前划分虽不能提升泛化性能 ,甚至可能导致泛化性能暂时下 ?但在其基础上进行的后续划分却有可能导致性能显提高 ; 预剪枝基于"贪心 "本质禁止这些分支展开7给预剪枝决策树带来了欠拟含风险。
3.2后剪枝
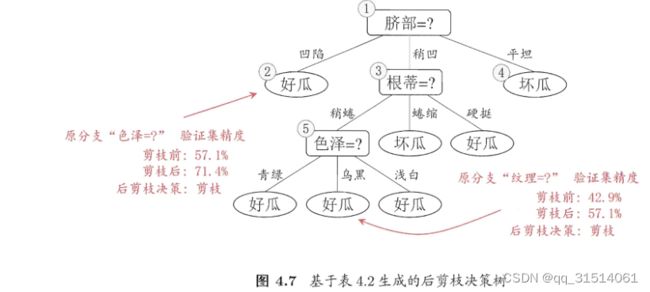
后剪枝决策树的欠拟合风险很小 ,泛化性能往往优于预剪枝决策树 . 但其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多 .
4.连续与缺失值
4.1连续值处理
最简单的方法是采取二分法对连续属性进行处理,
候选划分点集合:在区间[ a i , a i + 1 ) 中 取 任 意 值 所 产 生 的 划 分 结 果 相 同 a_i,a_{i+1})中取任意值所产生的划分结果相同 ai,ai+1)中取任意值所产生的划分结果相同,把区间 [ a i , a i + 1 ) [a_i,a_{i+1}) [ai,ai+1)中位点 a i + a i + 1 2 \frac{a_i+a_{i+1}}{2} 2ai+ai+1作为候选划分点。
G a i n ( D , a ) = m a x t ∈ T a G a i n ( D , a , t ) = m a x t ∈ T a E n t ( D ) − Σ λ ∈ ( − , + ) ∣ D t λ ∣ ∣ D ∣ E n t ( D t λ ) Gain(D,a) = max_{t\in T_a}Gain(D,a,t) =max_{t\in T_a}Ent(D) - \Sigma_{\lambda\in ({-,+})}\frac{|D_t^\lambda|}{|D|}Ent(D_t^\lambda) Gain(D,a)=maxt∈TaGain(D,a,t)=maxt∈TaEnt(D)−Σλ∈(−,+)∣D∣∣Dtλ∣Ent(Dtλ)
其 中 G a i n ( D , a , t ) 是 样 本 集 D 基 于 划 分 点 t 工 分 后 的 信 息 增 益 . 其 中Gain ( D,a, t ) 是 样 本 集 D 基 于 划 分 点 t 工 分 后 的 信 息 增 益 . 其中Gain(D,a,t)是样本集D基于划分点t工分后的信息增益.
于 是 , 我 们 就 可 选 择 使 G a i n ( D , α , t ) 最 大 化 的 划 分 点 于 是 , 我 们 就可 选 择 使 G a i n ( D, α,t ) 最 大 化 的 划 分 点 于是,我们就可选择使Gain(D,α,t)最大化的划分点
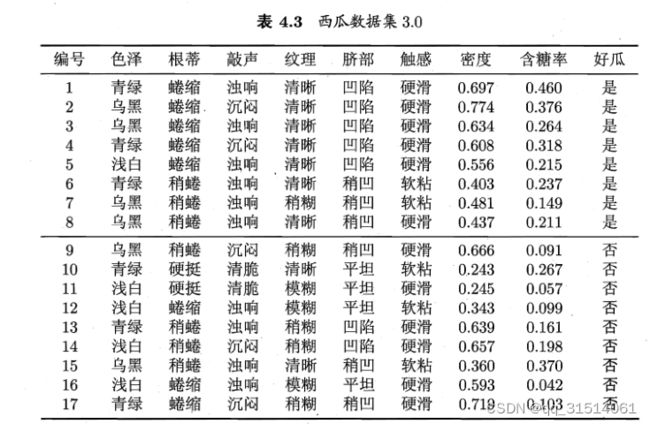
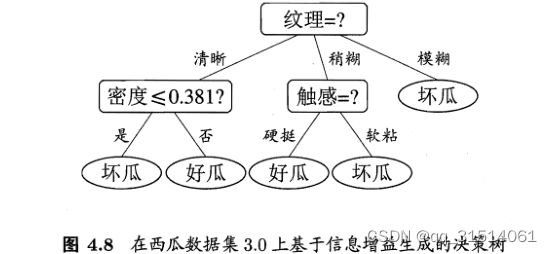
4.2缺失值处理
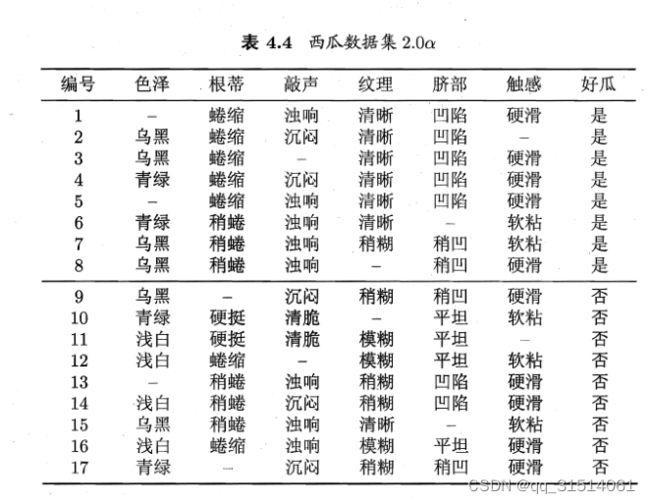
以 属 性 " 色 泽 " 为 例 , 该 属 性 上 无 缺 失 值 的 样 例 子 集 D ~ 包 含 编 号 为 以 属 性 " 色 泽 " 为 例 , 该 属 性 上 无 缺 失 值 的 样 例 子 集 \tilde {D}包 含 编 号 为 以属性"色泽"为例,该属性上无缺失值的样例子集D~包含编号为
( 2 , 3 , 4 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 14 , 15 , 16 , 17 ) 的 14 个 样 例 . 显 然 , D ~ 的 信 息 熵 为 ({ 2 , 3 , 4 , 6 , 7 , 8 , 9 , 1 0 , 1 1 , 1 2 , 1 4 , 1 5 , 1 6 , 1 7 } )的 1 4 个 样 例 . 显 然 ,\tilde {D}的 信 息 熵 为 (2,3,4,6,7,8,9,10,11,12,14,15,16,17)的14个样例.显然,D~的信息熵为
然后计算属性“色泽”所有样本取值的信息熵,从而得到“色泽”的信息增益。
再计算出所有属性在D上的信息增益,最大信息增益作为根节点。
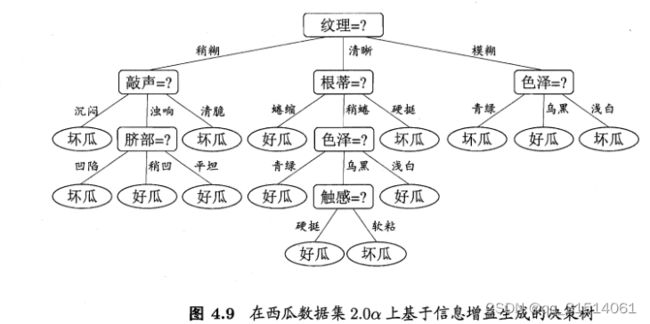
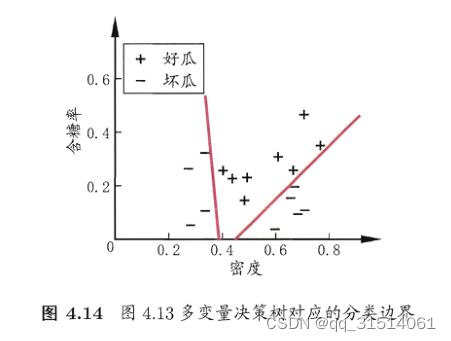
5.多变量决策树
决策树所形成的分类边界共同点:轴平行
缺点:在学习分类任务复杂时,很难获得较好的近似,时间开销大
解决方案:用属性组合替代属性进行测试,即对属性的线性组合测试,建立一个线性分类器。