matlab用最小欧氏距离,一种基于欧氏距离线性化逼近的设施选址最优化方法与流程...

本发明提供一种基于将欧氏距离线性化的设施最优选址的方法，它可用于在城市公共设施规划，针对现有的城市居民的分布，求解最优的垃圾仓库点坐标选址以及相应的居民分配，以减少居民与其所分配的垃圾仓库之间的运输成本，属于物流设施规划与选址领域。

二、

背景技术：

在物流设施规划领域，仓库选址问题是影响运输成本和效率的关键问题。。在经济发展过程中，我们经常需要设置一个或多个集散物质、传输信息或执行某种服务的“仓库”点，以便为其周边的节点传输信息或者提供服务。例如，在城市建设和规划商业中心、医院、消防站、停车场、垃圾回收站点等公共设施时，经常需要考虑将中心点选在什么位置才能使城市系统运行效能最佳。因此，在实际问题中，这些选址问题也就是关于设施最优选址的问题。如何选择服务站点的地址，在保证每个客户点被分配给合适的站点服务的前提下，使得所有客户点到其对应的服务点的总距离最短，是物流选址领域的一个难题。

该设计问题目前均为利用传统k-均值(即k-means)计算，但该方法需要预先给定初始中心点，计算结果受到初始中心点选择的影响，并且该方法的均值法计算中心点不能保证是最优距离中心，所以不能计算出最优解。本发明提出一种基于欧氏距离线性化的最优选址方法，该方法是一种全局优化的方法，保证了计算结果可以控制在任意小的误差范围之内，且避免了初始解对最终结果的影响。

三、

技术实现要素：

3.1发明目的

本项发明的目是提供一种基于欧氏距离线性化逼近的设施选址最优化方法，它是为物流选址的仓库点最优选址问题提供高效率的最优方案选择方法，使仓库点满足为周围客户点提供服务的要求，同时使所有客户点到其所分配的仓库的总距离最短。

3.2技术方案

首先对该问题进行规范化描述：某地区有n个分散客户，客户的坐标和需求均为已知。需要建立m个仓库(或服务设施)，各个仓库/设施具有相应的总容量/服务能力上限。求解最优的仓库坐标选址及客户分配，使得所有客户点到其所分配的仓库/设施的总距离最短。问题的决策变量就是该选择什么位置来建造仓库点以及每个仓库点为哪些客户点来提供服务，使得所有客户点到其所分配的仓库的总距离最短。

两点之间的欧式距离表示为其中和分别表示两点之间的x和y轴向距离。由于该距离表达式是非线性的，使仓库选址问题难以获得最优解。本专利设计了用一组切平面逼近的方法，来代替非线性欧式距离公式，并保证代替的误差可以在预先给定的任意小的误差范围ε之内。该组切平面逼近的表达式如下：

其中，q是切平面的数量，θ是两个相邻切平面的旋转夹角，均为常数，依赖于给定的小数ε。当ε值给定时，q和θ的计算公式如下：

上式中，计算符表示取大于等于x的最小整数。ε，θ与q的部分关系数据如下表1：

表1 ε，θ与q的关系表

下面先汇总定义若干的符号，便于对本专利的实施步骤进行准确描述：

基于以上符号定义，

本发明一种基于欧氏距离线性化逼近的设施选址最优化方法,由四步步骤完成，分别如下：

步骤一、数据预处理准备

本发明中，首先对二维平面内的客户点编号，编号值从1到N；其次，需要给出客户点的坐标，即用Xi表示客户点i的横坐标，Yi表示客户点i的纵坐标；接着给出待选仓库/设施的编号，编号值从1到K；最后为给定正整数q和给定角弧度θ赋值；

步骤二、建立线性数学规划模型

根据最优选址问题的思想，计算出最终选定的仓库点的坐标使得运输成本最少，即使得仓库点与所服务的客户点距离和最小，这里，将仓库点与所服务的客户点距离和称为目标函数；基于欧式距离线性化逼近的设施选址方法，建立线性数学规划模型；

其中，所述的“建立线性数学规划模型”，其建立的做法如下：

(1)最优化选址问题中使得每个客户点与其隶属的仓库点的距离和最小，并将这个距离和定义为目标函数；以此建立该问题的线性数学规划模型的目标函数，即把每个客户点i和它所属仓库点k之间的距离dik进行加和，且使得该距离和尽可能小。以此为基础建立如下目标函数：

(2)发明中的二维坐标平面内的每一个客户点均为需求点，仓库点旨在为客户点提供服务，所以限制条件需要保证每一个客户点i均有一个仓库点k为其提供服务，即对于任意一个客户点i，它能且只能被分配给一个仓库点k。建立约束条件1)：

1)

(3)本发明中的距离约束采用欧氏距离进行约束，所以在客户点i与仓库点k存在服务关系时，需要满足客户点i与所属仓库点k的x/y轴向距离不小于客户点i与所属仓库点k的横/纵坐标差，建立约束条件2)～5)：

2)

3)

4)

5)

(4)规定切平面数量切平面的数量q以及两个相邻切平面的旋转夹角θ，且由以上限制条件2)～5)可以得到dikxdiky的值，由此可以规定客户点i与仓库点k的欧氏距离dik，即建立约束条件6)：

6)

因此可以总结得出线性数学规划模型如下所示：

目标函数：

约束条件：

1)

2)

3)

4)

5)

6)

步骤三、求解模型

针对上述线性数学规划模型进行求解，考虑多种求解方式：(1)直接求解，利用单纯形法、分支定界方法、割平面法对该线性数学规划模型进行求解；(2)利用商业软件，如Lingo，CPLEX等，进行求解；

由于本数学规划模型是线性的，完全具备最优解求解可行性；

其中，所述的“模型”，是指在步骤二所建立的目标函数与约束条件1)～6)所组成的线性数学规划模型；

其中，所述的“求解模型”，选择利用AMPL语言调用CPLEX求解器求解模型，其求解的具体做法如下：

(1)输入所需要聚类的数据以及聚类基本参数，建立AMPL数据文件xxx.dat；

(2)建立AMPL模型文件xxx.mod，建立线性数学规划模型；

(3)建立AMPL批处理文件xxx.sh；

(4)使用AMPL调用批处理文件xxx.sh，开始求解；

步骤四、结果输出：确定最优的仓库点位置坐标

依据最终的计算结果，由模型的决策变量xk、yk和uik可以确定仓库点的坐标以及相应的客户隶属关系(如果uik＝1，则表示客户点i由仓库/设施k提供服务)，从而求得最优的目标函数值(即Total_Dis)，即仓库与客户的总距离。

通过以上步骤，本发明为物流选址的仓库点选址问题提供了全局最优选址方法，更高效地解决了实际生活中的物流设施选址问题。

3.3本发明的功效和优点

本发明有两点优点：

(1)与传统的K-means相比较，本方法避免了局部最优解受到初始解影响的问题；

(2)本方法采用线性规划进行优化，保证输出结果为全局最优解。

四、附图说明

图1本发明所述方法流程图。

图2传统k-means聚类方法的算例结果图。

图3基于本专利方法的算例结果图。

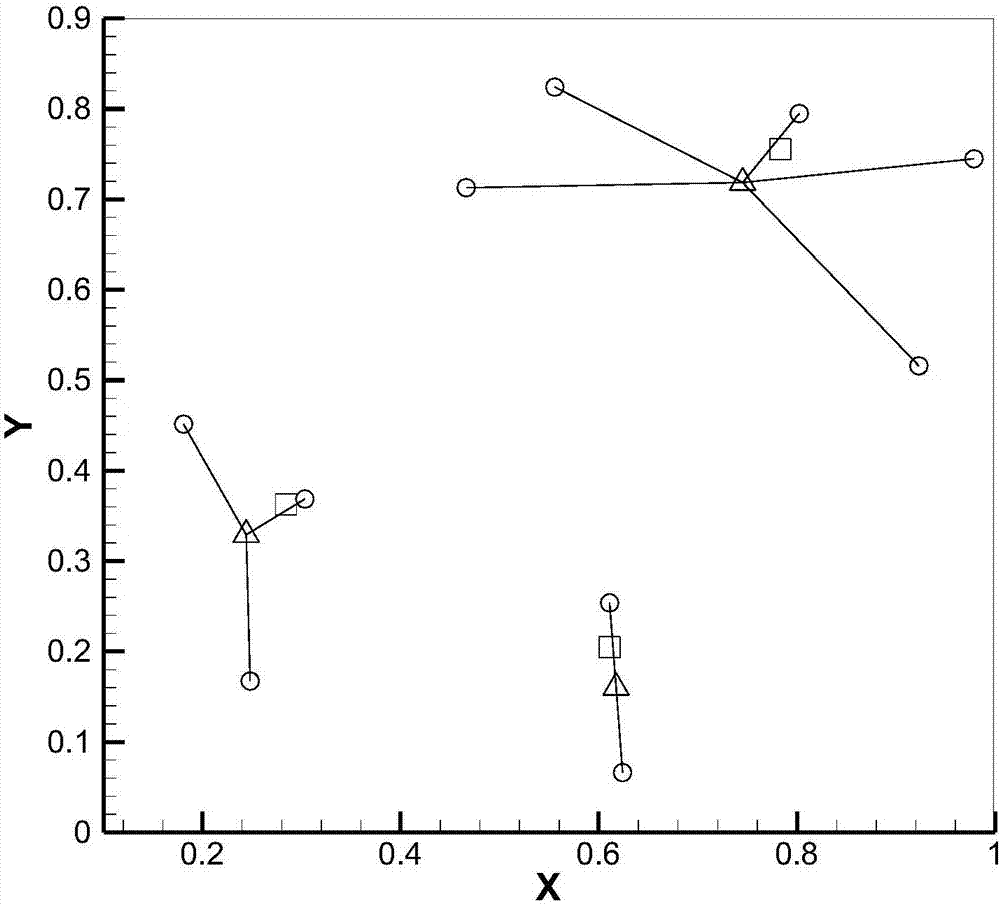
图中序号、符号、代号说明如下：

小方块 表示利用新方法计算得到的仓库点坐标

圆圈 表示二维平面内已知的客户点坐标

三角形 表示利用传统k-means方法计算得到的仓库点坐标

线段 表示计算得到的仓库点与客户点的所属关系

五、具体实施方式

下面以具体的算例说明本发明方法的具体实施方式。该算例为：在二维坐标平面内，有10个坐标点已知的客户，需要建立3个位置待定的服务站并分配服务关系，使总距离最短，假定服务点能力无约束。

本发明一种基于欧氏距离线性化逼近的设施选址最优化方法，见图1所示，其具体实施步骤如下：

步骤一、数据预处理

将二维平面内的10个客户点的坐标数据汇总至下表中：

表2 客户点坐标值

接着给仓库点赋值3，最后给出给定正整数q＝18和定角弧度θ＝0.0895赋值。

为了充分显示数学模型的可行性，我们采用描述并求解大规模复杂数学问题的建模语言(即AMPL)/数学规划模型求解器(即CPLEX)求解软件进行求解。AMPL是一种功能强大的综合代数语言，可以求解线性的数学规划模型。AMPL软件读入模型和数据文件后，按照执行策略，调用相关的求解器进行求解，本文中用到的求解器为CPLEX求解器。

步骤二、建立线性数学规划模型

目标函数：

约束条件：

1)

2)

3)

4)

5)

6)

步骤三、求解模型

以AMPL语言为基准，我们建立上述案例的数据文件p.dat:

按照给定的数学模型编写该案例的模型文件p.mod：

由于本数学模型是线性的，具有最优解求解可行性。本算例采用AMPL进行求解。编写相应的批处理文件p.sh：

最后利用AMPL调用批处理文件p.sh开始进行求解。

步骤四、结果输出

利用AMPL运行的最终计算结果如下：

根据AMPL运行的最终计算结果，可以得到最终的仓库点坐标以及客户点与仓库的相应供需关系，见图2所示。计算结果显示，利用改进后的模型求解出来的目标函数值，即所有客户点与其所属的仓库点的距离和为1.61633，而利用传统的k-means聚类方法得到的目标函数值为1.654592，最终的仓库点坐标以及客户点与仓库的相应供需关系，见图3所示。最后，为了便于观察，我们利用Tecplot绘图软件将改进后的模型以及传统k-means计算结果仓库与客户点分布与所属关系图绘成散点图。

基于相同的客户点，将计算结果与传统的k-means模型的计算结果进行比较，可以看出新方法获得的总距离小于传统k-means方法能获得的总距离。在散点图中也可以看出两种方法计算得到的仓库的位置坐标有所不同，本专利给出的方法能发现更佳的优化选址方案。