机器学习笔记-梯度下降法

梯度下降法

---

前言

  梯度下降法学习笔记，算法是用MATLAB来实现的，如有错误欢迎指出。

一、算法思想

1.1、原理举例

  梯度下降法（Geadient descent）是一种常用的一阶优化算法，是求解无约束优化问题最简单、最经典的方法之一，并且其在机器学习中使用非常非常广泛，不管是神经网络中的参数优化还是Boosting模型的构造中，都离不开梯度下降法，我们可以毫不夸张的说，梯度下降法是现代机器学习的血液。所以要想学好机器学习，就必须熟练掌握梯度下降算法。本文将从梯度下降法最常见的，同时也是最简单的应用中学习梯度下降法。
  如果抛开数学理论，我们可以这样去理解，在一座大山上，假设你站在半山腰上，你要在最短的时间内到达山底，并且不考虑下山时的安全问题，那么该如何下山呢？

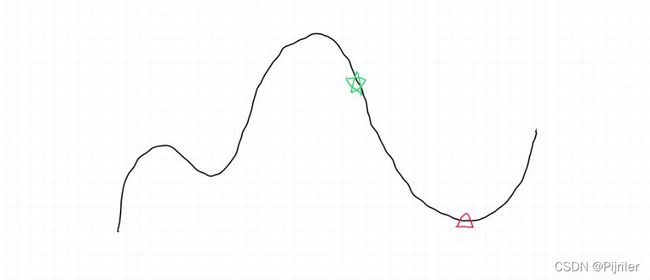
  比如你在上面绿色点的位置，你需要到达山底的红色三角形地区，最快的方法就是以当前的位置为基准，寻找该位置最陡峭的方向，然后沿着这个方向走一步，走一步之后，再次以新位置为基准，重新寻找最陡峭的方向，然后朝着这个方向再走一步，一直重复我们就可以到达最低点，并且这种行走方式一定是最快的。
从上面的描述其实也能看出，这样走将会面临几个问题：

• 如何求得在某一位置的最陡峭方向？

• 每一次走的步长应该有多大，如果步长大了会有什么影响？如果步长小了会有什么影响？

如果想要解决上面两个问题，我们就需要深入了解一下梯度下降法到底是如何运行的？

1.2、数学思想

  在梯度下降法算法中将会涉及到偏导数这一概念，这里不详细介绍偏导数。对于下山过程，要求在某点的最陡峭的方向，其实就是在该点的梯度。下面是梯度的含义：

  $f$在$P_0$的梯度方向就是$f$的值增长最快的方向，在下山中就是最陡峭的方向。只要我们一直朝着梯度方向走下去，就可以找到最小值了。
所以在上述问题一中，求在某点最陡峭的地方，其实就是求在该点的偏导数。对于问题二，在下山过程中，如果我们设置的步长比较短，则整个下山的过程就会变的很慢，耗时太长了；如果我们设置的步长比较长，那么可能导致所走的路线不是最佳路线，从而错过了最低点。这里的步长一般设置为0.1、0.01、0.001或其他的值比较合适。
既然说了梯度下降法是迭代算法，那么梯度下降法的迭代公式便给出：$$x^{(k+1)}=x^{(k)}+{\lambda }_k{d}^{(k)}$$
  其中$d^{(k)}$是搜索方向，当该方向为梯度方向是就是梯度下降法了（注意这里的$d^{(k)}$可以不是梯度方向，其他的方向我们以后再说）。
   梯度下降法的应用主要有两个方面：求解函数最小值和求解最优参数，其实后者也是求解最优值问题，只不过变换了一种说法，后面会说到。下面看算法应用。

二、算法应用

1.1、求函数最小值

  上面介绍梯度下降法之后，下面可以针对实例进行学习。
我们用梯度下降法来求解函数$z=\frac{1}{3}{x}^2+\frac{1}{2}{y}^2$的最小值。$\frac{1}{3}{x}^2+\frac{1}{2}{y}^2$求偏导的结果为：
$$z_x=\frac{2}{3}x$$
$$z_y=y$$

代码如下：

clc;
clear;
% 绘制图像
[x1, x2] = meshgrid(-10:0.5:10);
y1 = (1/3).*x1.^2 +( 1 / 2 ) .* x2.^2;
surf(x1,x2,y1);
grid on
hold on
% 梯度下降法求最小值
alpha = 0.01; % 步长
x_1 = 8; % 初始化x
x_2 = 8; % 初始化y
epsilon = 0.000001; % 迭代终止精度
while 1
    z = fun(x_1,x_2); % 求解函数值
    plot3(x_1,x_2,z,'*r'); % 画出散点图
    last_x = x_1; % 记录上一次x
    last_y = x_2; % 记录上一次y
    x_1 = x_1 - x_1 * alpha * (2/3); % 梯度下降法求解x_1
    x_2 = x_2 - x_2 * alpha * (1/2); % 梯度下降法求解x_2
    if (abs(fun(x_1,x_2)-fun(last_x,last_y)) < epsilon) % 判断
        break;
    end
end
z = abs(fun(x_1,x_2));
disp(['最小值为：',num2str(z)])

function [z] = fun(x1,x2)
z = (1/3)*x1^2+(1/2)*x2^2;
end

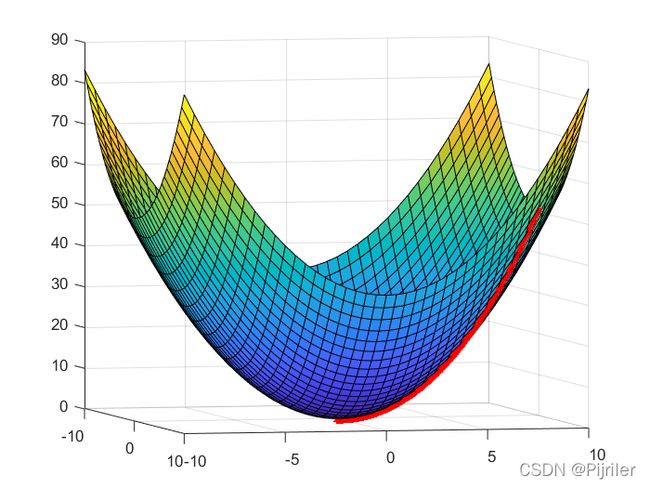
上述是求解给定函数的最小值，代码首先绘制了该函数的图像，然后从点（8，8）处用梯度下降法求解最小值，我设置的步长为0.01，结果见下图：

如果我设置步长为0.1，得到的结果图如下：

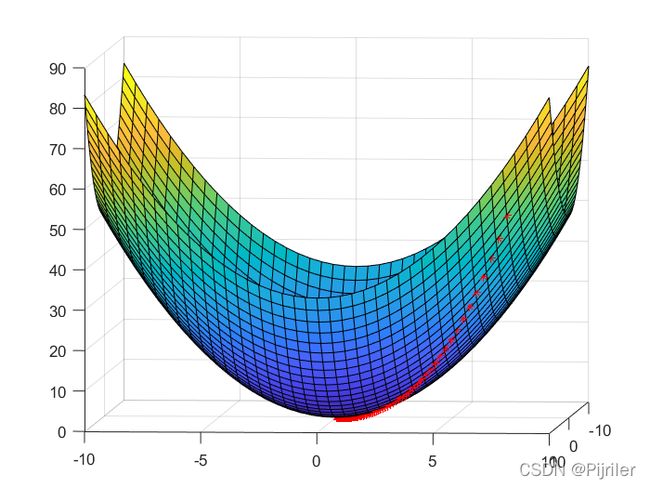
从图中可以看出，两张图运行的代码只是其步长不同，得到的结果是不一样的，但是最终都能成功找到最小值，只是第一张图运行的时间较长。

2.2、梯度下降法优化线性回归

  梯度下降法优化线性回归主要是对损失函数进行优化。首先来看这么一个问题，有两组数据，分别表示自变量和因变量，让我们找到一条最合适的直线方程来反映两组数据之间的关系，我们想到了一元回归，那么一元线性回归的方程多种多样，其通用的形式可以表示为：
$$y_i=w{x}_i+b$$
  上述的w是自变量的系数，b是截距，我们需要找到最合适的w和b，使得该直线最优，那么如何定义最优呢？下面又引入了一个Loss函数：
$$Loss=\frac{1}{2}\sum _{i=1}^n{(y_{ii}-(w{x}_i+b))}^2$$
  只要找到使得上述的Loss函数最小的参数w和b，我们就能找到最优的回归直线，而找到这条直线的方法就是梯度下降法。如果令损失函数为L，则对于此Loss函数的偏导为：
$$\frac{\partial L}{\partial w}=\sum _{i=1}^n{x}_i(y_{ii}-y_i)$$
$$\frac{\partial L}{\partial b}=\sum _{i=1}^n(y_{ii}-y_i)$$
  为了简化计算，那么可以将上述的两个偏导式合并起来迭代，也就是通过在矩阵中加一行常数列来进行矩阵计算
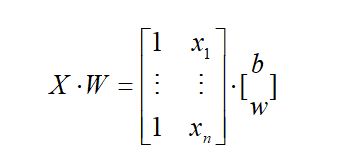这样做的目的就是方便编程实现计算。
代码如下：

clc;
clear;
tic
% 数据
X1 = [-10 -9 -9 -6.5 -5 -4.2 -3.9 -2.57 -1 0.32 0.1 1.36 1.88 2 2.58 3.2 3.54 3.5 4.02 4.65 5.02 5.79 6.44 6.5 7.65]';
Y1 = [-10.2 -12.01 -10.5 -10.3 -6.5 -5.9 -6.1 -5 -3.6 -1.45 -1.88 -0.64 -0.15 0.02 0.21 0.8 2 1.95 2.88 2.67 3.85 4.02 4.03 5.02 5.68]';
X = X1;
Y = Y1;
tX = X;%tX的作用只是为了创建detaW时使用
W = 0.1*ones(size(X,2)+1,1); % 初始化W矩阵
X = [ones(size(X,1),1),X]; % 创建X矩阵
k = 0;%迭代次数
alpha = 0.00005; % 步长
while true
    detaW = zeros(size(tX,2)+1,1);
    y = X*W; % 求解
    detaW = detaW + alpha*X'*(Y - y);%0.00005是学习速率
    W = W + detaW;
    k = k+1;
    if 1/2*( norm(Y - X*W) )^2 < 5 || k>10000 %如果误差小于5或者迭代次数大于10000则停止
        break;
    end
    draw(W,X1,Y1) % 调用绘图函数，测试代码
    hold off % 测试代码
    pause(0.01) % 测试代码
end
% 输出结果
disp(['w = ',num2str(W(2))])
disp(['b = ',num2str(W(1))])
toc

function draw(W,X,Y)
% 这里是测试代码，是为了显示动画过程
x = -10:0.1:8;
y = W(1)+W(2)*x;
plot(X,Y,'*r')
hold on
plot(x,y,'b')
axis([-10,8,-15,10])
title('回归效果图')
end

  上述代码中有几个需要解释的点，norm就是计算欧几里得范数，其实就是计算两点之间的距离，代码中年关键的几步运算都是通过矩阵实现的，draw是一个展示中间过程的绘图函数（不需要的话可以注释）。下面就是动态图：
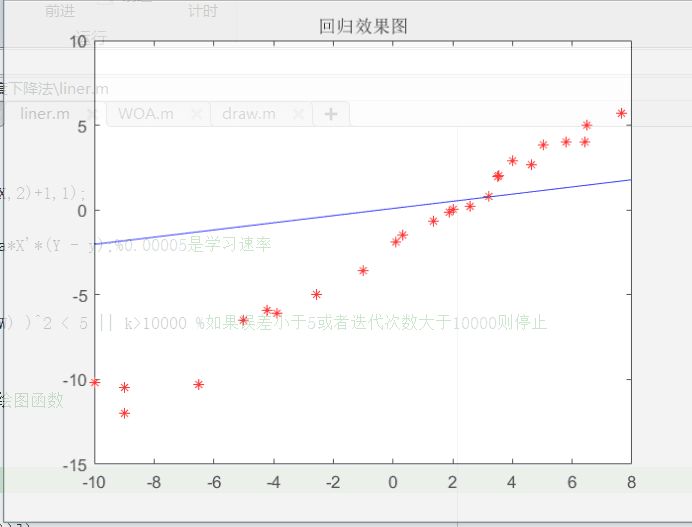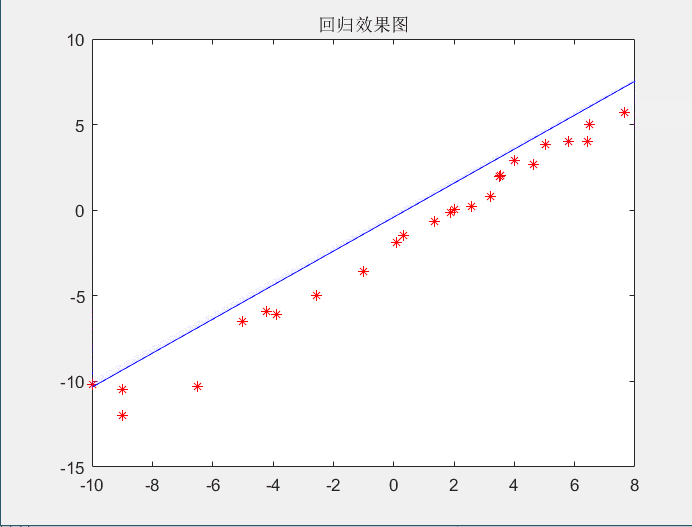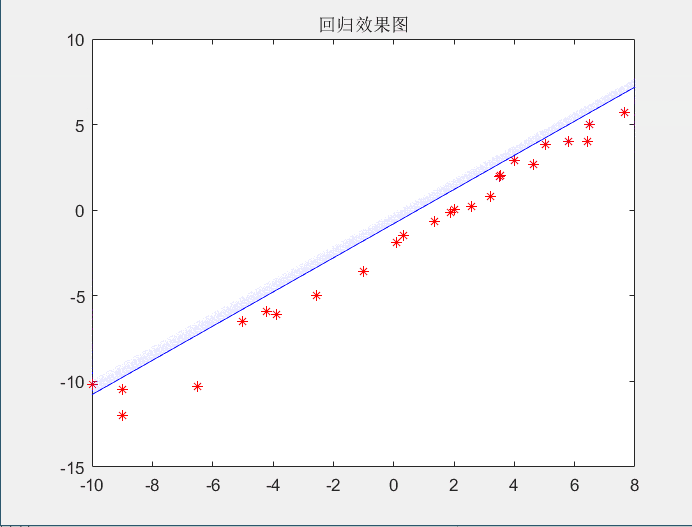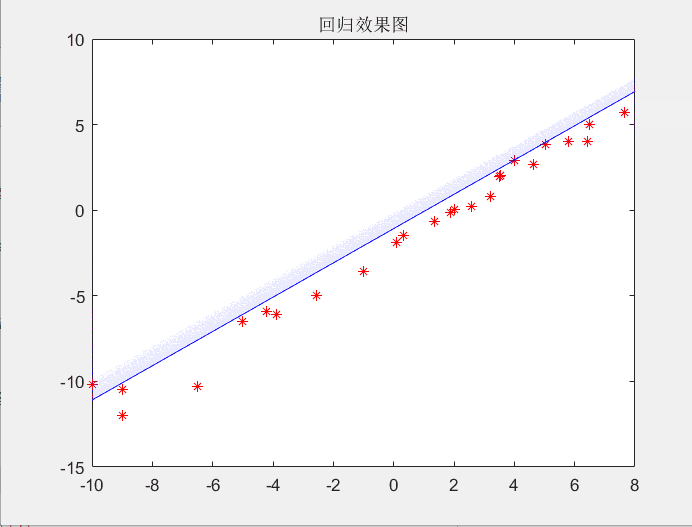回归的结果如下：


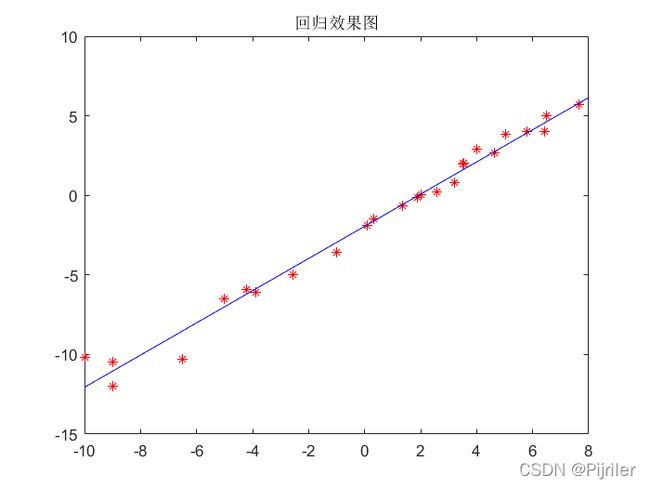
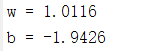
  即通过梯度下降法找到了最优的参数，其实整个过程就是一个不断迭代的过程，在不断迭代中寻找最优参数w和b。
  另外一点需要注意的是，梯度下降法也是有很多种类的，本文采用的是使用全部数据进行训练计算误差。但是当数据量特别大时，如果使用全部数据就会导致计算时间非常长，这时可以采用随机梯度下降法，使用单个或者少量的训练样本来更新参数，但是这样做也是有缺点的，找到的参数不一定就是最优的参数。总之有点像用精度换取时间的效果。

三、算法总结

  梯度下降法作为一个非常经典的优化算法，是入门机器学习必须要掌握的算法之一。在很多前沿的机器学习算法中都能看到梯度下降法的身影，算法使用的是一阶收敛，运行速度较慢，后面还会接触到牛顿法，这是一个二阶收敛算法，运行速度要比梯度下降法快很多，等后面学习到再整理吧。