动手学深度学习v2笔记-Day3-softmax回归

动手学深度学习v2

Day 3

---

0x00 softmax回归

• 回归和分类的区别

差异类型	回归	分类
输出值	单个连续输出	通常多个离散类别输出

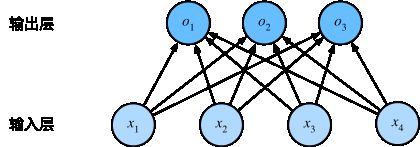
多个输入，多个输出
输出i是预测为第i类的置信度
softmax回归也是一种单层的神经网络，因为计算每个输出o完全取决于输入层的全部x

• softmax运算
  对于分类任务来讲，其实并不太关心结果的值，而更关心预测的所属类别的置信度是否够高，从而使结果足够正确

引入softmax函数如下：
$$\hat{y}=softmax(o)$$
其中
$${\hat{y}}_i=\frac{e^{o_i}}{{\sum }_1^k{e}^{o_k}}$$
这样保证了分子e的指数函数一定非负，而分母为分子的和，所有概率之和为1
真实label中的$y$只有一个分类为1，其余分类肯定为0，因此$y$和$\hat{y}$的差刚好可以作为损失函数

• 交叉熵损失函数
  我们沿用平方损失函数来验证分类结果，引用第一版书中的一个例子我们更直观的理解：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zCegatSz-1664621244240)(./day3-1.jpg)]
平方损失函数对于数值来说过于严格，而分类问题并不特别关心输出预测值的准确性

交叉熵（负号可以提出）：
$$H(p,q)=\sum _i^n-p_{i}log{q}_i$$
交叉熵损失函数（真实的y只有一项非零为1，因此求和可以直接干掉）：
$$l(y,\hat{y})=-\sum _i^n{y}_{i}log{\hat{y}}_i=-log{\hat{y}}_y$$

损失函数的梯度反映了真实概率和预测概率的区别

• 三种损失函数
  1.L2 loss 平方损失函数
  $$l(y,\hat{y})=\frac{1}{2}(y-\hat{y}{)}^2$$
  2.L1 loss 绝对值损失函数
  $$l(y,\hat{y})=|y-\hat{y}|$$
  3.Huber’s Robust loss
  $$l(y,\hat{y})\{\begin{array}{ll}|y-\hat{y}|-\frac{1}{2}& (|y-\hat{y}|>1)\\ \frac{1}{2}(y-\hat{y}{)}^2& \end{array}$$

0x01 手动实现

1.下载并且读取fashion-mnist数据集

import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l

# 读取数据集fashion-mnist
d2l.use_svg_display()

# 训练集、测试集 下载读取
trans = transforms.ToTensor()  # 利用这个方法将数据从PIL转换成tensor浮点型 且归一化
# 利用torch自带方法直接下载数据集
mnist_train = torchvision.datasets.FashionMNIST(root="../data", train=True, transform=trans, download=True)  # 训练集
mnist_test = torchvision.datasets.FashionMNIST(root="../data", train=False, transform=trans, download=True)  # 测试集

print(len(mnist_train), len(mnist_test))  # 6w 1w张
print(mnist_train[0][0].shape)  # 每一张图片被转换成这个shape的张量


# 返回读取数据的进程数
def get_dataloader_worker():
    return 8


# 读取一个批次的数据
batch_size = 256
train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_worker())

timer = d2l.Timer()
for X, y in train_iter:
    continue
print(f"{timer.stop():.2f} sec")

2.读取数据

# 随机读取256个图片
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)  

3.模型定义
softmax操作定义 exp(xij) / 求和exp(xij)
将单个元素换成了矩阵，每一行是一个o输出，那么分母就是对矩阵的每一行进行求和

def softmax(X):
    X_exp = torch.exp(X)  # 对每个元素进行exp操作
    partition = X_exp.sum(1, keepdim=True)  # 按列求和，每一列都累加到第一列，然后保留
    return X_exp / partition  # 广播机制

验证定义模型的正确性

X = torch.normal(0, 1, (2, 5))  # 定义一个两行五列的张量
X_ret = softmax(X)              # softmax
print(X_ret, X_ret.sum(1))      # 可以看到每行预测概率的和为1

4.定义softmax回归模型

num_inputs = 28 * 28  # 需要向量输入，简单处理就是将矩阵转换成向量 空间信息留到后面处理
num_outputs = 10  # 输出分类有十类
# 底层还是线性回归
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)  # 设置w需要记录梯度
b = torch.zeros(num_outputs, requires_grad=True)

def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)  # 内部可以看出还是线性回归，结果用softmax处理一下

5.从预测矩阵中拿出label的对应预测值

y = torch.tensor([0, 2])    # 原始数据的label 一个是0号种类 一个是2号种类
y_hat = torch.tensor([      # 预测矩阵
    [0.9, 0.1, 0.0],        # 预测正确
    [0.2, 0.5, 0.3]         # 预测错误
])
print(y_hat[[0, 1], y])     # 花式索引 -> 等同于取 y_hat[0, y[0]] 和 y_hat[1, y[1]] 很好理解

6.交叉熵损失函数

def cross_entropy(y_hat, y):
    return -torch.log(y_hat[range(len(y_hat)), y])
print(cross_entropy(y_hat, y))

验证交叉熵损失函数的正确性

def accuracy(y_hat, y):
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:  # 如果y是个矩阵
        y_hat = y_hat.argmax(axis=1)  # 将预测矩阵中每一行的最大值下标取出来 每一行最大值的索引
    cmp = y_hat.type(y.dtype) == y  # 转换数据类型并且比较
    return float(cmp.type(y.dtype).sum())  # 返回预测正确的样本数
print(accuracy(y_hat, y) / len(y))  # 0.5

7.评估精度

# 推广 评估任意模型在迭代器上的精度
class Accumulator:
    """在n个变量上累加"""
    def __init__(self, n):
        self.data = [0.0] * n

    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]

def evaluate_accuracy(net, iter):
    if isinstance(net, torch.nn.Module):
        net.eval()              # 不计算梯度了
    metric = Accumulator(2)
    for X, y in iter:
        metric.add(accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]
print(evaluate_accuracy(net, test_iter))  # 0.1118

8.训练

def train_epoch(net, train_iter, loss, updater):  # 这里的updater可以是之前的sgd函数 也可以是其他优化函数
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()
            updater.step()
            metric.add(float(l) * len(y), accuracy(y_hat, y), y.size().numel())
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])
            metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]


def train(net, train_iter, test_iter, loss, num_epochs, updater):
    for epoch in range(num_epochs):
        train_metrics = train_epoch(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
    train_loss, train_acc = train_metrics
    print(train_loss, train_acc, test_acc)
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc

# 学习率
lr = 0.1

# 还是sgd 小批量随机梯度下降
def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)

num_epochs = 10
train(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

9.验证

def predict(net, test_iter, n=6):  # @save
    for X, y in test_iter:
        break
    trues = d2l.get_fashion_mnist_labels(y)
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true + '\n' + pred for true, pred in zip(trues, preds)]
predict(net, test_iter)

0x02 pytorch实现

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

# 输出层是一个全连接层
# 定义模型
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))  # 这里使用flatten是为了在输入到linear层之前调整图片为向量

# flatten 将任何维度的tensor变成2d的tensor 0维度保留剩下的展开向量
def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)
        
net.apply(init_weights)

# 损失函数
loss = nn.CrossEntropyLoss()

# 优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.1)

# 训练
num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
d2l.predict_ch3(net, test_iter)