用Scikit-learn和TensorFlow进行机器学习（二）

一个完整的机器学习项目

主要步骤：

1. 项目概述。
2. 获取数据。
3. 发现并可视化数据， 发现规律。
4. 为机器学习算法准备数据。
5. 选择模型， 进行训练。
6. 微调模型。
7. 给出解决方案。
8. 部署、 监控、 维护系统。

一、真实数据

流行的开源数据仓库：

• UC Irvine Machine Learning Repository
• Kaggle datasets
• Amazon’s AWS datasets

准入口（ 提供开源数据列表）

• http://dataportals.org/
• http://opendatamonitor.eu/
• http://quandl.com/

其它列出流行开源数据仓库的网页：

• Wikipedia’s list of Machine Learning datasets
• Quora.com question
• Datasets subreddit

二、项目概述

StatLib 的加州房产价格数据集（1990年），利用加州普查数据， 建立一个加州房价模型。 这个数据包含每个街区组的人口、 收入中位数、 房价中位数等指标。学习并根据其他指标预测任何街区的房价中位数。

1、划定问题

问题
（1）商业目标是什么？如何使用、并从模型受益？
==》划定问题、选择算法、评估模型的性能指标 。

（2）现在的解决方案效果如何？
==》参考性能、解决问题。

本项目：监督学习中的回归任务

2、选择性能指标（损失函数）

（1）回归任务

RMSE（均方根误差）
$$RMSE(X,h)=\sqrt{\frac{1}{m}\sum _{i=1}^m(h(x^{(i)})-y^{(i)}{)}^2}$$
其中，$m$ 表示RMSE的数据集中的实例数量；$h$表示系统的预测函数，也称假设（hypothesis）；$x^{(i)}$ 表示数据集第 $i$ 个实例的所有特征值（不含标签）的向量，$y^{(i)}$ 是它的标签；$X$ 表示数据集中所有实例的所有特征值（不含标签）的矩阵，每一行是一个实例，第 $i$ 行是 $x^{(i)}$ 的转置，记作$x^{(i)T}$。

（2）平均绝对误差（MAE，Mean Absolute Error）

适用：存在许多异常的值
$$MAE(X,h)=\frac{1}{m}\sum _{i=1}^m|h(x^{(i)})-y^{(i)})|$$

（3）范数

• L2范数（欧几里得范数的RMSE）：$||\cdot |{|}_2或||\cdot ||$
• L1范数（曼哈顿范数）：绝对值(MAE)和$||\cdot |{|}_1$
• 一般化，包含 $n$ 个元素的向量 $v$ 的 $L_k$ 范数（K阶闵氏范数）
  $$||v|{|}_k=(|v_0{|}^k+|v_1{|}^k+...+|v_n{|}^k{)}^{\frac{1}{k}}$$
• L0范数：非零元素个数；
• L${}_{\infty }$:切比雪夫范数：向量中最大的绝对值.

范数的指数越高， 就越关注大的值而忽略小的值。 这就是为什么 RMSE 比 MAE 对异常值更敏感。 但是当异常值是指数分布的（ 类似正态曲线） ， RMSE 就会表现很好。

3、核实假设

三、获取数据

import os
import tarfile
from six.moves import urllib
import pandas as pd

DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml/master/"
HOUSING_PATH = "datasets/housing"
HOUSING_URL = DOWNLOAD_ROOT + HOUSING_PATH + "/housing.tgz"

## 获取数据
def fetch_housing_data(housing_url = HOUSING_URL, housing_path = HOUSING_PATH):
	## os.path.isdir()函数判断某一路径是否为目录
    if not os.path.isdir(housing_path):
        os.makedirs(housing_path)
    ## 路径拼接
    tgz_path = os.path.join(housing_path,"housing.tgz")
    urllib.request.urlretrieve(housing_url, tgz_path)
    ## 解压文件：打开、提取、关闭
    housing_tgz = tarfile.open(tgz_path)
    housing_tgz.extractall(path=housing_path)
    housing_tgz.close()

## 加载数据，返回DataFrame对象
def load_housing_data(housing_path = HOUSING_PATH):
    csv_path = os.path.join(housing_path,"housing.csv")
    return pd.read_csv(csv_path)

fetch_housing_data()
housing = load_housing_data()

相关函数解析

1、os模块

• os.path.isdir(path) ——判断路径是否为目录，存在返回True
• os.path.join(path1[, path2[, …]])——将一个或多个路径正确地连接起来
• os.makedirs(path, mode=0o777)——递归创建目录

2、urllib.request.urlretrieve

urllib.request.urlretrieve(url, filename=None, reporthook=None, data=None)
将URL地址的文件复制到本地filename的路径中

四、查看数据结构

1、数据信息查看

对DataFrame对象

• head() 方法：查看前5行数据；
• info() 方法：快速查看数据描述，特别是总行数、 每个属性的类型和非空值的数量
• housing[“ocean_proximity”].value_counts() ——该项（ocean_proximity）中的类别统计
• describe()——数值属性的概况

##  DataFrame 的 head() 方法查看该数据集的前5行
print(housing.head())
## info()方法：快速查看数据的描述
## 特别是总行数、 每个属性的类型和非空值的数量
print(housing.info())

输出结果

   longitude  latitude       ...         median_house_value  ocean_proximity
0    -122.23     37.88       ...                   452600.0         NEAR BAY
1    -122.22     37.86       ...                   358500.0         NEAR BAY
2    -122.24     37.85       ...                   352100.0         NEAR BAY
3    -122.25     37.85       ...                   341300.0         NEAR BAY
4    -122.25     37.85       ...                   342200.0         NEAR BAY

[5 rows x 10 columns]

RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
longitude             20640 non-null float64
latitude              20640 non-null float64
housing_median_age    20640 non-null float64
total_rooms           20640 non-null float64
total_bedrooms        20433 non-null float64
population            20640 non-null float64
households            20640 non-null float64
median_income         20640 non-null float64
median_house_value    20640 non-null float64
ocean_proximity       20640 non-null object
dtypes: float64(9), object(1)
memory usage: 1.6+ MB
None

==》total_bedrooms 20433 non-null float64
==》存在207个空值需要处理

print(housing["ocean_proximity"].value_counts())  ## 该项中的类别统计
print('----------'*5)
print(housing.describe())  ## 数值属性的概况

输出结果

<1H OCEAN     9136
INLAND        6551
NEAR OCEAN    2658
NEAR BAY      2290
ISLAND           5
Name: ocean_proximity, dtype: int64
--------------------------------------------------
          longitude         ...          median_house_value
count  20640.000000         ...                20640.000000
mean    -119.569704         ...               206855.816909
std        2.003532         ...               115395.615874
min     -124.350000         ...                14999.000000
25%     -121.800000         ...               119600.000000
50%     -118.490000         ...               179700.000000
75%     -118.010000         ...               264725.000000
max     -114.310000         ...               500001.000000

[8 rows x 9 columns]

注意：describe() 中忽略空值，eg：total_rooms为20433

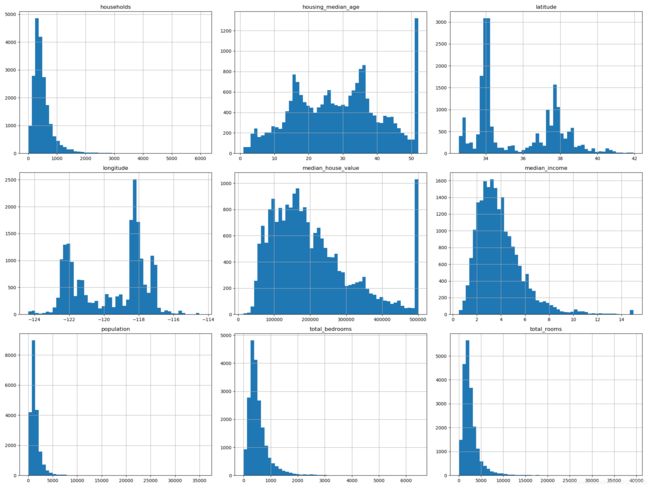
2、可视化描述——每个属性的柱状图

柱状图（的纵轴）展示了特定范围的实例的个数。

• hist() 方法：对完整数据调用该方法，可画出每个数值属性的柱状图

import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(20,15))
plt.show()

分析可知：

1. 收入中位数貌似不是美元（ USD）。数据经过预处理：过高收入中位数的会变为 15（ 实际为 15.0001） ， 过低的会变为 5（ 实际为 0.4999）
2. 房屋年龄中位数和房屋价值中位数也被设了上限。由于房屋价值中位数是标签，则预测的价格不会超过这个界限。==》需要重新确认
3. 属性值有不同的度量。==》特征缩放
4. 许多柱状图的尾巴很长，分布不均==》变换到正态分布

五、数据准备

为了避免数据透视偏差，创建测试集

1、测试集

（1）实现（造轮子）

def split_train_test(data, test_ratio):
    shuffled_indices = np.random.permutation(len(data))
    test_set_size = int(len(data) * test_ratio)
    test_indices = shuffled_indices[:test_set_size]
    train_indices = shuffled_indices[test_set_size:]
    return data.iloc[train_indices], data.iloc[test_indices]

train_set, test_set = split_train_test(housing, 0.2)
print(len(train_set), "train +", len(test_set),"test")

输出结果

16512 train + 4128 test

（2）知识点

1、random中shuffle与permutation的区别

函数 shuffle 与 permutation 都是对原来的数组进行重新洗牌（即随机打乱原来的元素顺序）；

区别：shuffle 直接在原来的数组上进行操作，改变原来数组的顺序，无返回值。而 permutation 不直接在原来的数组上进行操作，而是返回一个新的打乱顺序的数组，并不改变原来的数组。

a = np.arange(12)
print a
np.random.shuffle(a)
print a
print 
a = np.arange(12)
print a
b = np.random.permutation(a)
print b
print a

输出结果

[ 0  1  2  3  4  5  6  7  8  9 10 11]
[11  6  4 10  3  0  7  1  9  2  5  8]
 
[ 0  1  2  3  4  5  6  7  8  9 10 11]
[10  4  8 11  1  7  6  2  0  9  5  3]
[ 0  1  2  3  4  5  6  7  8  9 10 11]

（3）存在问题

程序再次运行，则产生不同的测试集。

解决方法：

1. 保存第一次运行的结果，之后过程加载。
2. 设置随机数生成器种子 np.random.seed(2019)，可使得每次产生相同的 shuffled indices

若数据集更新，则上述方法均失败。
==》
解决方法：使用每个实例的ID来判定这个实例是否应该放入测试集（ 假设每个实例都有唯一并且不变的ID）。
例如， 你可以计算出每个实例ID的哈希值， 只保留其最后一个字节， 如果该值小于等于 51（ 约为 256 的 20%） ， 就将其放入测试集。 这样可以保证在多次运行中， 测试集保持不变， 即使更新了数据集。 新的测试集会包含新实例中的 20%， 但不会有之前位于训练集的实例。

1. 如果使用行索引作为唯一识别码， 你需要保证新数据都放到现有数据的尾部， 且没有行被删除。
2. 用最稳定的特征来创建唯一识别码。 例如，一个区的维度和经度用最稳定的特征来创建唯一识别码。 例如， 一个区的维度和经度。

import hashlib
def test_set_check(identifier, test_ratio, hash)
    return hash(np.int64(identifier)).digest()[-1] < 256 * test_ratio

def split_train_test_by_id(data, test_ratio, id_column, hash=hashlib.md5)
    ids = data[id_column]
    in_test_set = ids.apply(lambda id_:test_set_check(id_, test_ratio, hash))
    return data.loc[~in_test_set],data.loc[in_test_set]
    
## 方法1：将行索引作为ID
housing_with_id = housing.reset_index()   # adds an `index` column
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index")

## 方法2：使用经度纬度作为唯一标识度
housing_with_id["id"] = housing["longitude"] * 1000 + housing["latitude"]
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "id")

（4）实现（sklearn）

train_test_split()

• random_state 参数:随机生成器种子设置；
• 可以将种子传递给多个行数相同的数据集，可以在相同的索引上分割数据集

适用于：数据集很大时（尤其是和属性相比）；

train_set, test_set = train_test_split(housing, test_size=0.2, random_state=2019)

若数据集不大，则会有采样偏差的风险
==》分层采样（stratified sampling）
==》每个分层都要有足够的实例

（5）分层采样

loc、iloc、ix区别：https://blog.csdn.net/u012736685/article/details/86610946

## 收入中位数除以 1.5（ 以限制收入分类的数量）,ceil返回不小于x的最小整数
housing["income_cat"] = np.ceil(housing["median_income"] / 1.5)
## 将所有大于5的分类归入类别5
housing["income_cat"].where(housing["income_cat"] < 5, 5.0, inplace=True)

## 分层采样——StratifiedShuffleSplit
from sklearn.model_selection import StratifiedShuffleSplit

split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=2019)
print(split)
for train_index, test_index in split.split(housing, housing["income_cat"]):
    strat_train_set = housing.loc[train_index]
    strat_test_set = housing.loc[test_index]

## 验证数据集中收入分类的比例
print(housing["income_cat"].value_counts()/len(housing))

## 删除income_cat属性，使数据回到初始状态
for set in (strat_train_set, strat_test_set):
    set.drop(["income_cat"], axis=1, inplace=True)

输出结果

StratifiedShuffleSplit(n_splits=1, random_state=2019, test_size=0.2,
            train_size=None)
3.0    0.350581
2.0    0.318847
4.0    0.176308
5.0    0.114438
1.0    0.039826
Name: income_cat, dtype: float64

六、数据探索和可视化、发现规律

1、地理数据可视化

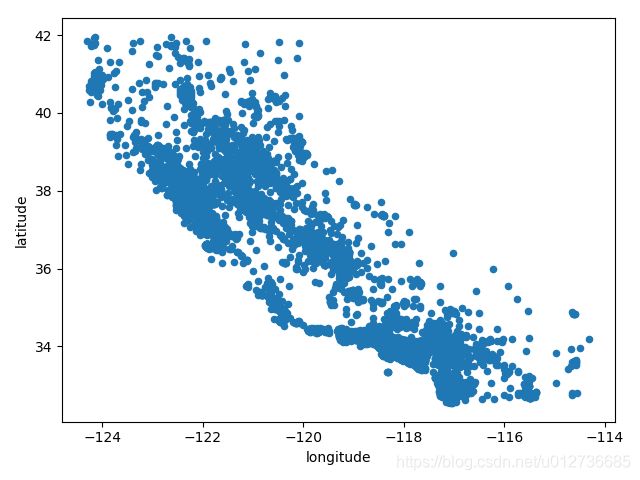
（1）地理位置可视化

存在地理信息==》散点图

## 存在地理信息==》散点图
housing.plot(kind="scatter", x="longitude", y="latitude")
plt.show()

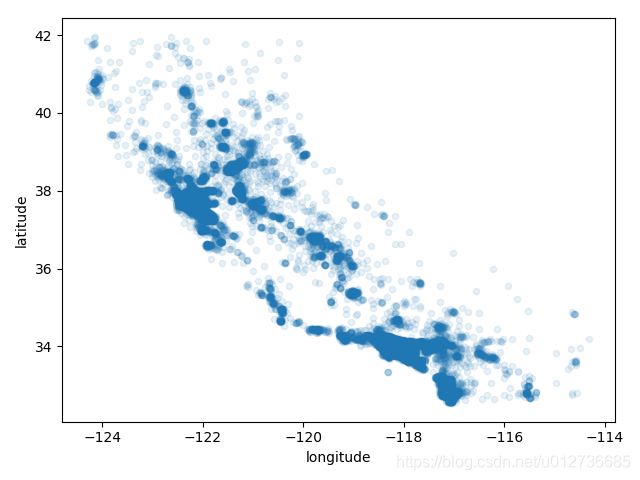
## 显示高密度区域的散点图
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
plt.show()

（2）基本地理位置的房价可视化

关于房价散点图：每个圈的半径表示街区的人口（ 选项 s ）， 颜色代表价格（选项 c）。 我们用预先定义的名为 jet 的颜色图（选项 cmap）， 它的范围是从蓝色（低价）到红色（高价）

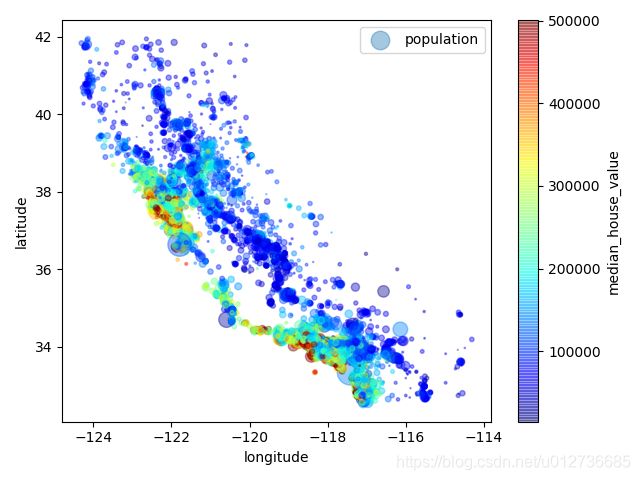
==》房价和位置（ 比如， 靠海） 和人口密度联系密切

2、查找关联

（1）corr()

corr()方法计算出每对属性间的标准相关系数（ standard correlation coefficient， 也称作皮尔逊相关系数）

相关系数的范围是 [-1, 1]。 当接近 1 时， 意味强正相关； 当相关系数接近 -1 时， 意味强负相关。

corr_matrix = housing.corr()
# 每个属性和房价中位数的关联度
corr_matrix_house_value = corr_matrix["median_house_value"].sort_values(ascending=False)
print(corr_matrix_house_value)

输出结果

median_house_value    1.000000
median_income         0.687894
total_rooms           0.135763
housing_median_age    0.108102
households            0.067783
total_bedrooms        0.050826
population           -0.024467
longitude            -0.049271
latitude             -0.139948
Name: median_house_value, dtype: float64

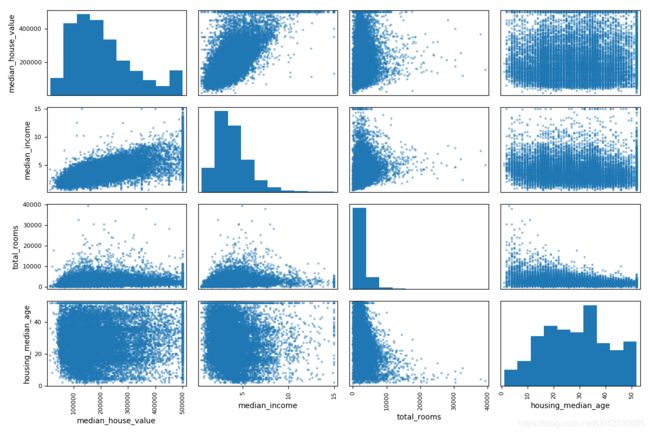
（2）scatter_matrix()

pandas 的 scatter_matrix()：画出每个数值属性对每个其他数值属性的图。eg：有 $d$ 个属性，则有 $d^2$ 个图。

只关注几个与房价中位数最有可能相关的属性

from pandas.plotting import scatter_matrix

attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"]
scatter_matrix(housing[attributes],figsize=(12, 8))
plt.show()

（3）本项目

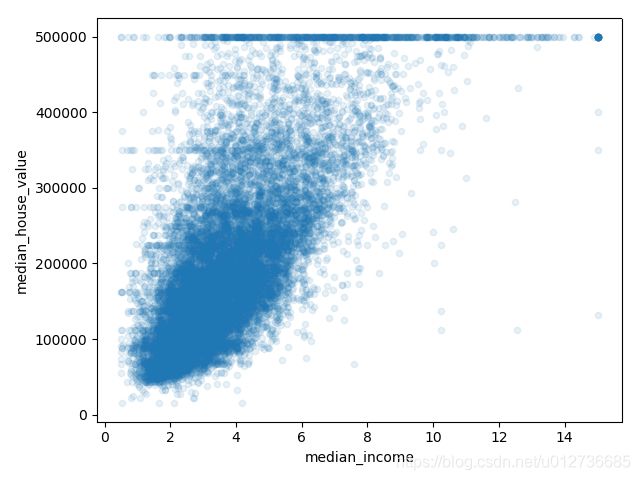
最有希望用来预测房价中位数的属性是收入中位数。

housing.plot(kind="scatter", x="median_income", y="median_house_value", alpha=0.1)
plt.show()

==》

• 相关性非常高。向上趋势，不是非常分散
• 最高价位于500000美元
• 存在不是太明显的直线： 450000 美元、350000 美元、 280000 美元…

3、属性组合试验==》新属性

思考：目标与已有属性的关联

housing["room_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"] = housing["population"]/housing["households"]
# 查看相关矩阵
corr_matrix = housing.corr()
corr_matrix_house_value = corr_matrix["median_house_value"].sort_values(ascending=False)
print(corr_matrix_house_value)

输出结果

median_house_value          1.000000
median_income               0.687894
room_per_household          0.146690
total_rooms                 0.135763
housing_median_age          0.108102
households                  0.067783
total_bedrooms              0.050826
population                 -0.024467
population_per_household   -0.025585
longitude                  -0.049271
latitude                   -0.139948
bedrooms_per_room          -0.253689
Name: median_house_value, dtype: float64

==》新的 bedrooms_per_room 属性与房价中位数的关联更强。 卧室数/总房间数的比例越低， 房价就越高。

七、为机器学习算法准备数据

数据转换函数，适用于任何数据集上==》复用

注意：drop() 创建数据的备份，不改变原始数据。

训练集（干净的）的划分

housing = strat_train_set.drop("median_house_value", axis=1)
housing_labels = strat_train_set["median_house_value"].copy()

1、数据清洗

特征缺失

（1）DataFrame对象

• dropna() 方法：去掉缺失的样本
• drop() 方法：去掉缺失的属性
• fillna() 方法：赋值填充

housing.dropna(subset=["total_bedrooms"])
housing.drop("total_bedrooms", axis=1)
median = housing["total_bedrooms"].median()
housing["total_bedroom"].fillna(median)

（2）Scikit-Learn 提供的 Imputer 类处理缺失值

1. 创建一个 Imputer 实例对象，指定用某属性的中位数来替换该属性所有的缺失值；
2. 准备数据：数值型
3. fit() 方法拟合训练数据；
4. transform()方法将数据转换
5. 类型转换（非必需）：ndarray->DataFrame

from sklearn.preprocessing import Imputer

## 1.实例化Imputer对象
imputer = Imputer(strategy="median")

## 2.准备数据
## 由于只有数值属性才有中位数==》不包括 ocean_proximity 的数据副本
housing_num = housing.drop("ocean_proximity", axis = 1)

## 3.fit()拟合数据
imputer.fit(housing_num)
## 中位数位于实例变量 statistics_ 中
print(imputer.statistics_)
print(housing_num.median().values)  ## 等价
## 转换，结果类型为 numpy 数组

## 4.transform()转换数据
X = imputer.transform(housing_num)
# print(type(X))     # 

## 5.数据格式转换
## 格式转换：numpy数组 -> DataFrame格式
housing_tr = pd.DataFrame(X, columns=housing_num.columns)

（3）scikit-learn设计原则

一致性：所有对象接口简单且一致。

• 估计器（estimator）：基于数据集对参数进行估计的对象。fit() 方法。
• 转换器（transformer）：转换数据集。transform() 方法。
• 预测器（predictor）：根据数据集作出预测。predict() 方法对新实例的数据集做出相应的预测。score() 方法对预测进行衡量。

可检验：超参数访问
①实例的public变量直接访问（eg：imputer.strategy）；
②实例变量名加下划线（eg：imputer.statistics_）
类不可扩散
可组合
合理的默认值

2、处理文本和类别属性

（1）将文本标签转换为数字

==》
单列文本特征：LabelEncoder
多列文本特征：factorize()

from sklearn.preprocessing import LabelEncoder

encoder = LabelEncoder()
housing_cat = housing["ocean_proximity"]
housing_cat_encoded = encoder.fit_transform(housing_cat)
print(housing_cat_encoded[:20])

## 多个文本特征列——factorize()方法
housing_cat_encoded, housing_categories = housing_cat.factorize()
print(housing_cat_encoded[:20])


## 查看映射表
print(encoder.classes_)

输出结果

[0 0 0 1 4 0 0 1 1 0 0 0 0 4 1 4 0 4 0 0]
[0 0 0 1 2 0 0 1 1 0 0 0 0 2 1 2 0 2 0 0]
['<1H OCEAN' 'INLAND' 'ISLAND' 'NEAR BAY' 'NEAR OCEAN']

存在问题：ML算法会认为临近的值比两个疏远的值更相似。
==》One-Hot Encoding

（2）One-Hot Encoding（独热编码）

sklearn 提供 OneHotEncoder 编码器，将整数分类值变为one-hot。

注意：fit_transform() 用于2D数组。

from sklearn.preprocessing import OneHotEncoder

encoder = OneHotEncoder()
housing_cat_1hot = encoder.fit_transform(housing_cat_encoded.reshape(-1, 1))
print(type(housing_cat_1hot))

## 转换为 NumPy 数组：toarray()
print(housing_cat_1hot.toarray())

输出结果是一个SciPy稀疏矩阵，只存储非零元素位置，可以像一个2D数据那样使用。

（3）LabelBinarizer（文本分类=》one-hot）

应用于标签列的转换，输出结果是 ndarray 数组

参数：spare_output=True 可得到稀疏矩阵

## 一步转换：由文本分类到one-hot编码
from sklearn.preprocessing import LabelBinarizer


# encoder = LabelBinarizer(sparse_output=True) # 结果为稀疏矩阵 
encoder = LabelBinarizer()  # 结果为 ndarray 数组
housing_cat_1hot = encoder.fit_transform(housing_cat)
print(housing_cat_1hot)     # ndarray数组

（4）CategoricalEncoder类（文本分类=》one-hot）

## from sklearn.preprocessing import CategoricalEncoder

cat_encoder = CategoricalEncoder()
housing_cat_reshaped = housing_cat.values.reshape(-1, 1)
housing_cat_1hot = cat_encoder.fit_transform(housing_cat_reshaped)
print(housing_cat_1hot)

3、自定义转换器

sklearn是依赖鸭子类型的（而不是继承），所以创建一个类并执行三个方法：fit()、transform() 和 fit_transform()。

若通过添加 TransformMixin 作为基类，可以容易获得最后一个；
若添加 BaseEstimator 作为基类（ 且构造器中避免使用 *args 和 **kargs），你就能得到两个额外的方法（get_params() 和 set_params() ） ， 二者可以方便地进行超参数自动微调。

from sklearn.base import BaseEstimator, TransformerMixin
rooms_ix, bedrooms_ix, population_ix, household_ix = 3, 4, 5, 6

class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
    # 超参数 add_bedrooms_per_room
    def __init__(self, add_bedrooms_per_room=True):
        self.add_bedrooms_per_room = add_bedrooms_per_room
    def fit(self, X, y=None):
        return self
    def transform(self, X, y=None):
        rooms_per_household = X[:, rooms_ix] / X[:, household_ix]
        population_per_household = X[:, population_ix] / X[:, household_ix]
        if self.add_bedrooms_per_room:
            bedrooms_per_room = X[:, bedrooms_ix] / X[:, household_ix]
            return np.c_[X, rooms_per_household, population_per_household, bedrooms_per_room]
        else:
            return np.c_[X, rooms_per_household, population_per_household]
attr_adder = CombinedAttributesAdder(add_bedrooms_per_room=False)
housing_extra_attribs = attr_adder.transform(housing.values)

超参数 add_bedrooms_per_room ， 默认设为 True （ 提供一个合理的默认值很有帮助）。 这个超参数可以让你方便地发现添加了这个属性是否对机器学习算法有帮助。 更一般地， 你可以为每个不能完全确保的数据准备步骤添加一个超参数。

4、特征缩放（重要）

通常来说，当 输入的数值属性量度不同时，ML算法的性能都不会好。==》特征缩放

• 线性函数归一化（Min-Max scaling）
• 标准化（standardization）

（1）线性函数归一化（Min-Max scaling）

也称归一化（normalization）：值被转变、 重新缩放，
直到范围变成 0 到 1。

手动方法：通过减去最小值，然后再除以最大值与最小值的差值，来进行归一化。

sklearn中MinMaxScaler。参数：feature_range，该参数可以改变范围

（2）标准化

首先减去平均值（ 所以标准化值的平均值总是 0），然后除以方差，使得到的分布具有单位方差。

标准化不会限定值到某个特定的范围，受异常值的影响很小。

sklearn中StandardScaler

注意：缩放器只能向训练集拟合，而不是向完整的数据集。==》使用缩放器转换训练集和测试集

5、转换流水线

sklearn中Pipeline类，可以实现一系列的转换。定义步骤顺序的名字/估计器对的列表

（1）数值属性Pipeline

示例：数值属性的小流水线

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

num_pipeline = Pipeline([
    ('imputer', Imputer(strategy="median")),
    ("attribs_adder", CombinedAttributesAdder()),
    ('std_scaler', StandardScaler()),
])
housing_num_tr = num_pipeline.fit_transform(housing_num)

（2）多Pipeline——FeatureUnion

完整的处理数值和类别属性的Pipeline

from sklearn.pipeline import FeatureUnion
from sklearn_features.transformers import DataFrameSelector

num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]

num_pipeline = Pipeline([
    ('selector', DataFrameSelector(num_attribs)),
    ('imputer', Imputer(strategy="median")),
    ('attribs_adder', CombinedAttributesAdder()),
    ('std_scaler', StandardScaler()),
])
cat_pipeline = Pipeline([
    ('selector', DataFrameSelector(cat_attribs)),
    ('label_binarizer', CategoricalEncoder()),
])
full_pipeline = FeatureUnion(transformer_list=[
    ("num_pipeline", num_pipeline),
    ("cat_pipeline", cat_pipeline),
])

housing_prepared = full_pipeline.fit_transform(housing)
print(housing_prepared.toarray())
print(housing_prepared.shape)

输出结果

[[ 0.82875658 -0.77511404 -0.45095287 ...  0.          0.
   0.        ]
 [-1.23341542  0.81679116 -1.00737005 ...  0.          0.
   0.        ]
 [ 0.71890722 -0.76572227 -0.21248836 ...  0.          0.
   0.        ]
 ...
 [ 0.95857854 -0.81737701 -1.24583456 ...  0.          0.
   0.        ]
 [ 1.25317454 -1.16956843 -0.92788188 ...  0.          0.
   0.        ]
 [-1.57794295  1.26290029 -0.21248836 ...  0.          0.
   0.        ]]
(16512, 16)

也可自定义转换器

## 自定义转换器
from sklearn.base import BaseEstimator, TransformerMixin

class DataFrameSeclector(BaseEstimator, TransformerMixin):
    def __init__(self, attribute_names):
        self.attribute_names = attribute_names
    def fit(self, X, y=None):
        return self
    def transform(self, X):
        return X[self.attribute_names].values

六、选择并训练模型

在训练集上训练和评估

1、线性回归模型

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)

## 部分数据的测试
some_data = housing.iloc[:5]
some_labels = housing_labels.iloc[:5]
some_data_prepared = full_pipeline.transform(some_data)
some_predict = lin_reg.predict(some_data_prepared)
print("Predictions:\t", some_predict)
print("Labels:\t", list(some_labels))

## 计算 rmse
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
print(lin_rmse)

输出结果：68669.95539695179。
==》欠拟合
==》原因：特征没有提供足够多的信息来做出一个好的预测， 或者模型并不强大。
==》改进方面：

• 更强大的模型；
• 更好的特征；
• 去掉模型上的限制（正则化过多）

2、决策树回归

可以发现数据中复杂的非线性关系。

from sklearn.tree import DecisionTreeRegressor

tree_reg = DecisionTreeRegressor()
tree_reg.fit(housing_prepared, housing_labels)

housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
print(tree_rmse)

输出结果：0.0
==》模型严重过拟合

3、使用交叉验证做评估

常用方法：

• 使用函数 train_test_split 来分割训练集，训练集、验证集、测试集；
• 交叉验证：K折交叉验证(K-fold cross-validation)

三种模型：LR、决策树回归、随机森林回归的交叉验证

from sklearn.model_selection import cross_val_score

def display_scores(scores):
    print("Scores:", scores)
    print("Mean:", scores.mean())
    print("Standard deviation:", scores.std())
tree_scores = cross_val_score(tree_reg, housing_prepared, housing_labels,
                         scoring="neg_mean_squared_error", cv=10)
tree_rmse_scores = np.sqrt(-tree_scores)
display_scores(tree_rmse_scores)
print("---------"*4)

lin_scores = cross_val_score(lin_reg, housing_prepared, housing_labels,
                             scoring="neg_mean_squared_error", cv=10)
lin_rmse_scores = np.sqrt(-lin_scores)
display_scores(lin_rmse_scores)

print("----------"*4)
from sklearn.ensemble import RandomForestRegressor

forest_reg = RandomForestRegressor()
forest_reg.fit(housing_prepared, housing_labels)
forest_scores = cross_val_score(forest_reg, housing_prepared, housing_labels,
                             scoring="neg_mean_squared_error", cv=10)
forest_rmse_scores = np.sqrt(-forest_scores)
display_scores(forest_rmse_scores)

输出结果

Scores: [70822.23047418 71152.99791399 70767.60492457 69174.95049637
 72622.10092238 69728.83829471 66654.37564791 70054.61150426
 69280.92370212 74907.80020052]
Mean: 70516.64340810133
Standard deviation: 2082.183642340021
------------------------------------
Scores: [ 70442.28429562  69617.76028683  64863.46929222  66655.75946003
  69140.8730363   69983.30339185 168909.38005488  69421.92167885
  69133.39326617  72247.69581812]
Mean: 79041.58405808883
Standard deviation: 30017.242297265897
----------------------------------------
Scores: [51250.15421462 51550.55413458 50450.47743545 49847.26652631
 52580.05326516 53701.83169532 53254.54063586 53543.98321435
 51547.57591096 54118.87113271]
Mean: 52184.53081653092
Standard deviation: 1390.819447961666

解决过拟合可以通过简化模型， 给模型加限制（ 即， 规整化） ， 或用更多的训练数据。

4、模型保存

保存模型，方便后续的使用。要确保有超参数和训练参数，以及交叉验证评分和实际的预测值。

• python中 pickle模块
• sklearn中 sklearn.externals.joblib

from sklearn.externals import joblib

## dump
joblib.dump(forest_reg, "my_model.pkl")
## load
my_model_loaded = joblib.load("my_model.pkl")

七、模型微调

1、网格搜索——GridSearchCV

告诉 GridSearchCV 要试验有哪些超参数， 要试验什么值， GridSearchCV 就能用交叉验证试验所有可能超参数值的组合。

from sklearn.model_selection import GridSearchCV

param_grid = [
    {'n_estimators':[3, 10, 30], 'max_features':[2, 4, 6, 8]},
    {'bootstrap':[False], 'n_estimators':[3, 10], 'max_features':[2, 3, 4]},
]
forest_reg = RandomForestRegressor()
grid_search = GridSearchCV(forest_reg, param_grid, cv=5, scoring='neg_mean_squared_error')
grid_search.fit(housing_prepared, housing_labels)

## 获得参数的最佳组合
print(grid_search.best_params_)
## 获取最佳的估计器
print(grid_search.best_estimator_)
## 得到评估得分
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
    print(np.sqrt(-mean_score), params)

输出结果

{'max_features': 6, 'n_estimators': 30}

RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
           max_features=6, max_leaf_nodes=None, min_impurity_decrease=0.0,
           min_impurity_split=None, min_samples_leaf=1,
           min_samples_split=2, min_weight_fraction_leaf=0.0,
           n_estimators=30, n_jobs=1, oob_score=False, random_state=None,
           verbose=0, warm_start=False)
           
64779.22756782305 {'max_features': 2, 'n_estimators': 3}
55261.50069764705 {'max_features': 2, 'n_estimators': 10}
52361.133957894344 {'max_features': 2, 'n_estimators': 30}
59781.94102696423 {'max_features': 4, 'n_estimators': 3}
51630.24533131685 {'max_features': 4, 'n_estimators': 10}
49858.27456556619 {'max_features': 4, 'n_estimators': 30}
58919.396444692095 {'max_features': 6, 'n_estimators': 3}
51688.869762217924 {'max_features': 6, 'n_estimators': 10}
49706.749116241685 {'max_features': 6, 'n_estimators': 30}
58580.04583044209 {'max_features': 8, 'n_estimators': 3}
51316.919104777364 {'max_features': 8, 'n_estimators': 10}
49836.46832731868 {'max_features': 8, 'n_estimators': 30}
61793.95302711806 {'bootstrap': False, 'max_features': 2, 'n_estimators': 3}
54158.3503067861 {'bootstrap': False, 'max_features': 2, 'n_estimators': 10}
59230.45284179936 {'bootstrap': False, 'max_features': 3, 'n_estimators': 3}
51852.484216931596 {'bootstrap': False, 'max_features': 3, 'n_estimators': 10}
57991.28909825388 {'bootstrap': False, 'max_features': 4, 'n_estimators': 3}
51045.46342488829 {'bootstrap': False, 'max_features': 4, 'n_estimators': 10}

注意：如果 GridSearchCV 是以（ 默认值） refit=True 开始运行的， 则一旦用交叉验证找到了最佳的估计器， 就会在整个训练集上重新训练。 这是一个好方法， 因为用更多数据训练会提高性能。

扩展：可以像超参数一样处理数据准备的步骤。
eg：网格搜索可以自动判断是否添加一个你不确定的特征（ 比如， 使用转换器 CombinedAttributesAdder 的超参数 add_bedrooms_per_room ） 。 它还能用相似的方法来自动找到处理异常值、 缺失特征、特征选择等任务的最佳方法。

2、随机搜索——RandomizedSearchCV

适用于：超参数的搜索空间很大时，它通过选择每个超参数的一个随机值的特定数量的随机组合。

优点：

• 可设置搜索次数，控制超参数搜索的计算量；
• 例如运行1000次，就可探索每个超参数的1000个不同的值。

3、集成方法

将表现最好的模型组合起来。

4、分析最佳模型和它们的误差

feature_importances = grid_search.best_estimator_.feature_importances_
print(feature_importances)

print("------------"*4)
# 将重要性分数和属性名放到一起
extra_attribs = ["rooms_per_hhold","pop_per_hhold","bedrooms_per_room"]
cat_one_hot_attribs = list(encoder.classes_)
attributes = num_attribs + extra_attribs + cat_one_hot_attribs
print(sorted(zip(feature_importances, attributes), reverse=True))

输出结果

[9.16165799e-02 7.26401545e-02 3.98792143e-02 1.86271235e-02
 1.60430050e-02 1.73210114e-02 1.56763513e-02 3.50405341e-01
 6.66148402e-02 1.06807615e-01 2.44534680e-02 1.61218489e-02
 1.50921731e-01 2.34067365e-04 4.78731917e-03 7.85032928e-03]
------------------------------------------------
[(0.350405341367853, 'median_income'), (0.15092173111904114, 'INLAND'), (0.10680761466868184, 'pop_per_hhold'), (0.09161657987744719, 'longitude'), (0.07264015445556546, 'latitude'), (0.06661484017044574, 'rooms_per_hhold'), (0.0398792143039908, 'housing_median_age'), (0.024453467989156156, 'bedrooms_per_room'), (0.01862712349143468, 'total_rooms'), (0.01732101143541747, 'population'), (0.0161218489227077, '<1H OCEAN'), (0.01604300503679087, 'total_bedrooms'), (0.015676351349524945, 'households'), (0.007850329279641088, 'NEAR OCEAN'), (0.00478731916701119, 'NEAR BAY'), (0.00023406736529078728, 'ISLAND')]

八、用测试集评估系统

过程：

• 从测试集得到预测值和标签；
• 运行 full_pipeline 转换数据（ 调用 transform() ， 而不是 fit_transform() ！ ）;
• 再用测试集评估最终模型：

final_model = grid_search.best_estimator_

X_test = strat_test_set.drop("median_house_value", axis=1)
y_test = strat_test_set["median_house_value"].copy()

X_test_prepared = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)

final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)

评估结果通常要比交叉验证的效果差一点

九、启动、 监控、 维护系统

准备：接入输入数据源、编写测试、监控代码、新数据滚动