计算机图形学-光栅图形学算法
光栅图形学算法
直线段的扫描转换算法
主要有三个算法:1)数值微分法,2)中点画线法,3)Bresenham算法
数值微分法(DDA)
引进图形学中一个很重要的思想—增量思想。
y i = k x i + b , y i + 1 = k x i + 1 + b = k ( x i + 1 ) + b = k x i + b + k = y i + k y_i=kx_i+b,\\ y_{i+1}=kx_{i+1}+b\\ =k(x_i+1)+b\\ =kx_i+b+k\\ =y_i+k yi=kxi+b,yi+1=kxi+1+b=k(xi+1)+b=kxi+b+k=yi+k
当前步的y值等于前一步的 y y y 值加上斜率 k k k,这样就把原来一个乘法和加法变成了一个加法。
改进方法:1)改进效率,2)直线方程类型方面进行改。
中点画线法
每次在最大位移方向上走一步,而另一个方向是走步还是不走步要取决于中点误差项的判断。
如下面这张图中, a b s ( k ) ∈ [ 0 , 1 ] abs(k) \in [0,1] abs(k)∈[0,1],每次在 x x x 方向上加1, y y y 方向上加1或不变需要判断。

改进方法:用增量思想改写,使算法成为整数加法的运算。
Bresenham算法
1)通过各行、各列像素中心构造一组虚拟网格线;
2)按照直线起点到终点的顺序,计算直线与各垂直网格线的交点;
3)根据误差项的符号确定该列象素中与此交点最近的像素;
4)把这个算法的效率也搞到整数加法。
Bresenham算法很像DDA算法(加斜率),但应用范围广泛。
总结
DDA:每步做一个加法。
中点画线法:每步做一个整数加法。
Bresenham算法:更一般的算法,兼顾效率和适用性。
多边形的扫描转换
光栅图形的一个基本问题是把多边形的顶点表示转换为点阵表示。这种转换称为多边形的扫描转换。
X-扫描线算法:按扫描线顺序,计算扫描线与多边形的相交区间,再用要求的颜色显示这些区间的像素,即完成填充工作。关键问题是求交。

改进的多边形扫描转换算法思想:1)扫描线,2)增量
既考虑扫描线是连贯的,也要考虑到多边形的连贯性。
新的数据结构:活性边表(AET)
活性边表的数据结构如下:

新边表(NET),用来存放多边形的边的信息:
![]()
每做一次新的扫描线时,对已有的边进行处理:
1.是否被去除掉;
2.如果不被去除,第二就要对它的数据进行更新;
3.看有没有新的边进来,插入排序。
上述做法避免了求交运算。
边缘填充算法:
思想:按任意顺序处理多边形的每条边。
步骤:
1)对每条边求出该边与扫描线的交点;
2)每一条扫描线上交点右方的所有像素取补;
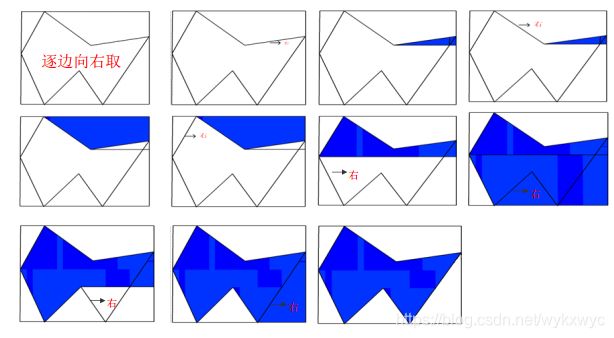
问题:边缘填充算法简单,但对于复杂图,每个像素可能被访问多次。
解决:减少边缘填充法访问像素的次数,采用栅栏填充算法。
栅栏填充算法:
栅栏:一条过多边形顶点且与扫描线垂直的直线。
做法:把多边形分为两半,将交点与栅栏之间的像素取补
边界标志算法:
做法:对多边形边界所经过的象素打上标志,将其围住区域上色。
优势:
1)不必建立维护边表以及对它进行排序;
2)适合硬件实现;
3)执行速度比有序边表算法快1到2个数量级。
区域填充算法
概念:将种子点扩展到整个区域内的过程,概念上和BFS非常相像。
反走样算法
走样:
1)锯齿形;
2)图形中包含微小的物体,微小物体四舍五入被舍弃;
3)动画中时隐时现,闪烁。
解决反采样的方法:
1)采用分辨率更高的显示设备,但以4倍的存储和转换时间为代价;
2)采用某种形式的模糊,这里面又分为了非加权区域采样方法和加权区域采样方法。
非加权区域采样方法
按面积给像素赋值,有以下缺点:
a.亮度与面积成正比,而与位置无关(面积可能一样,相交部分更接近中心应该越亮);
b.直线上相邻像素会有较大的灰度差;
加权区域采样方法
根据相交区域与像素中心的距离来决定其权重。
裁剪算法
屏幕显示只是图形的一部分,确定哪些落在显示区之内,哪些落在显示区之外,选择的过程就成为裁剪。
点的裁剪
比较简单,直接进行比较边界。
直线裁剪
直线裁剪有三种:1)Cohen-Sutherland算法,2)中点分割算法,3)Liang-Barsky裁剪算法
Cohen-Sutherland算法:每条线的端点都以4位二进制码进行编码,然后进行二进制的或、与运算,根据结果进行不同的操作。比较适合大部分线段完全可见/大部分线段完全不可见。
中点分割算法:通过二分逼近确定直线段与窗口的交点。
Liang-Barsky裁剪算法:
a.用参数方程表示一条直线:
x = x 1 + u ⋅ ( x 2 − x 1 ) = x 1 + Δ x ⋅ u y = y 1 + u ⋅ ( y 2 − y 1 ) = y 1 + Δ y ⋅ u u ∈ [ 0 , 1 ] x=x_1+u\cdot(x_2-x_1)=x_1+\Delta x\cdot u\\ y=y_1+u\cdot(y_2-y_1)=y_1+\Delta y\cdot u\\ u \in [0,1] x=x1+u⋅(x2−x1)=x1+Δx⋅uy=y1+u⋅(y2−y1)=y1+Δy⋅uu∈[0,1]
b.把被裁减的直线段看成是一条有方向的线段,把窗口的四条边分成两类,入边和出边。
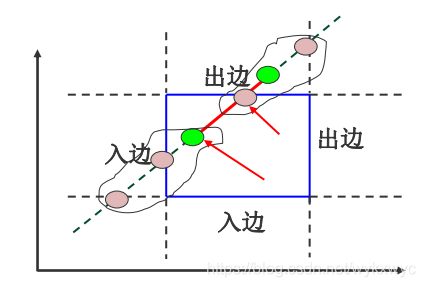
c.然后求取直线的参数方程与边界直线的交点 u u u 值: u l , u r , u b , u t u_l,u_r,u_b,u_t ul,ur,ub,ut。
u 1 = m a x ( 0 , u t , u b ) , u 2 = m i n ( 1 , u t , u r ) u_1=max(0,u_t,u_b),\\ u_2=min(1,u_t,u_r) u1=max(0,ut,ub),u2=min(1,ut,ur)
Cohen-Sutherland算法和Liang-Barsky裁剪算法只能适用于矩形窗口。
多边形的裁剪
Sutherland-Hodgeman多边形裁剪算法:将多边形边界作为一个整体,每次用窗口的一条边对要裁剪的多边形和中间结果多边形进行裁剪,分而治之。
利用Sutherland-Hodgeman裁剪算法对凸多边形进行裁剪可以获得正确的裁剪结果,但是对凹多边形会产生多余的线段,如下图:

文字裁剪
文字裁剪有三种:1)串精度裁剪,2)字符精度裁剪,3)笔划/像素精度裁剪
串精度裁剪:当字符串中的所有字符都在裁剪窗口内时,就全部保留它,否则舍弃整个字符串。
字符精度裁剪:在进行裁剪时,任何与窗口有重叠或落在窗口边界以外的字符都被裁剪掉。
笔划/像素精度裁剪:将笔划分解成直线段对窗口作裁剪。
三种不同的方式如下图:


