机器学习 卷积神经网络 Convolutional Neural Network(CNN)
Convolutional Neural Network(CNN)— 卷积神经网络
CNN专用在影像上的神经网络,目的是作影像辨识、影像分类,即通过输入的影像,输出影像中的内容。
对于CNN,有两种解释方法:
Explanation 1:Neuron Version
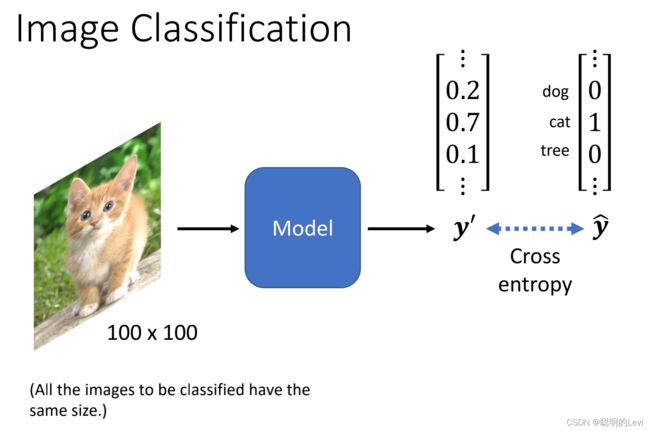
如上图所示:
输入:image(假设大小固定为100x100,若非100x100的图片则需要rescale后再放入影像辨识系统中)
输出:y’(vector)
目标输出:y^ (每一个目标需要表示成one-hot vector,在向量中数值为1的维度对应所属目标,且维度长度决定现在的模型可辨识不同种类目标的数目)在上图的y^所表示的目标向量中,猫所对应的维度为1,表示目标结果为猫。
此时计算Cross entropy,cross entropy越小,y‘与y^越接近,即输出结果与目标结果越接近。
机器输出结果y‘是如何从图像转化为向量
 3-D tensor:三维矩阵对于machine而言,一张图片是一个3-D tensor,3维:图片的高、图片的宽、图片的channel数目。
3-D tensor:三维矩阵对于machine而言,一张图片是一个3-D tensor,3维:图片的高、图片的宽、图片的channel数目。
当图片是彩色的,channel数目为3(RGB三色)
当图片是黑白的,channel数目为1
基于彩色图片来讨论,将每一个channel中的pixel展开列出成一个向量,向量中每一维存储的数值,代表某一个颜色的强度。
如何辨识向量中的图案
通过Fully connected Network以辨识向量中的图案
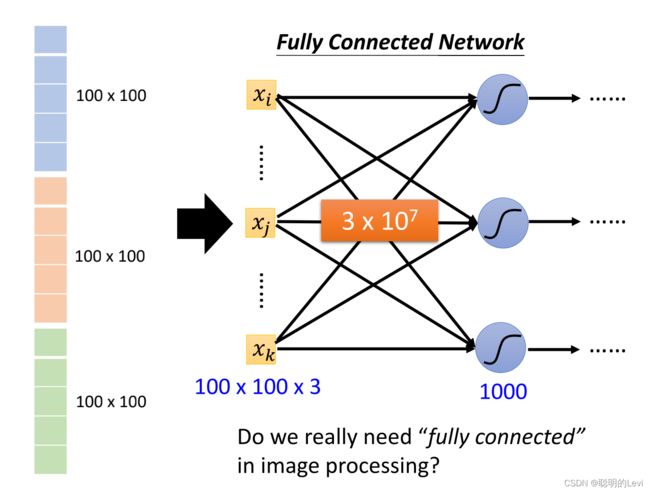
每一个neuron和输入向量中每一个数值都会有一个weight。例如上图中,输入向量的长度为3x100x100,neuron数目为1000,则第一层conventional network的参数数目为3x107。
参数数目过高,容易导致overfitting,我们事实上不需要这么多参数
如何减少参数,降低model弹性
Simplification 1: 采用receptive field

在影像辨识中,只需要辨识影像中的关键特征,不需要观测整张图片中的所有细节特征。不同的neuron可用于辨识不同的特征。Simplification 1解决了此问题。
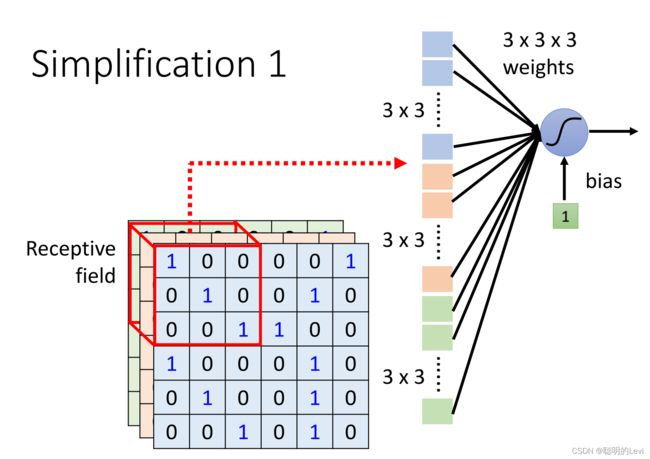
每一个neuron只考虑自己的Receptive field。如上图中:这一个neuron只考虑每个channel中3x3的区域。

上图中给出三个问题:
(1)Q:不同neurons是否可以有不同大小的receptive fields? A:可以,Receptive field的大小是自己定义的
(2)Q:neuron可否只考虑某些channel? A:可以,某些pattern或许只在一种颜色上出现
(3)Q:Receptive field可否不是正方形?A:可以,receptive field的形状和大小都是自定义的
此外,多个neuron可以同时守备一个receptive field,不同receptive fields之间可以重叠。通常,同一个receptive field会由一组neurons去守备。
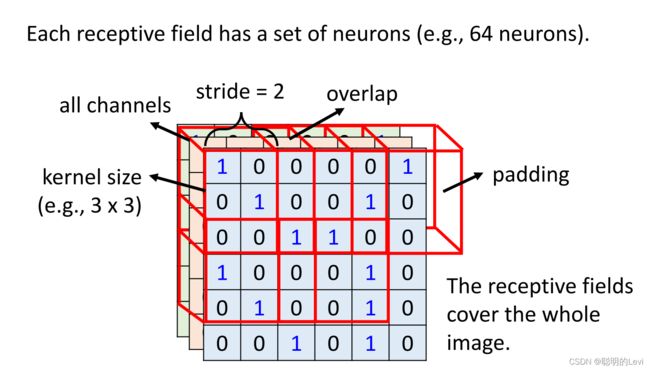
在上图中,左上角3x3的正方形为一个receptive field,由一组neurons守备。将该field向其他方向移动,移动跨度stride设为2,则转化为下一个receptive field。receptive field将会覆盖整张图片,因此可能会出现field超出image的情况,将超出部分补0来解决。
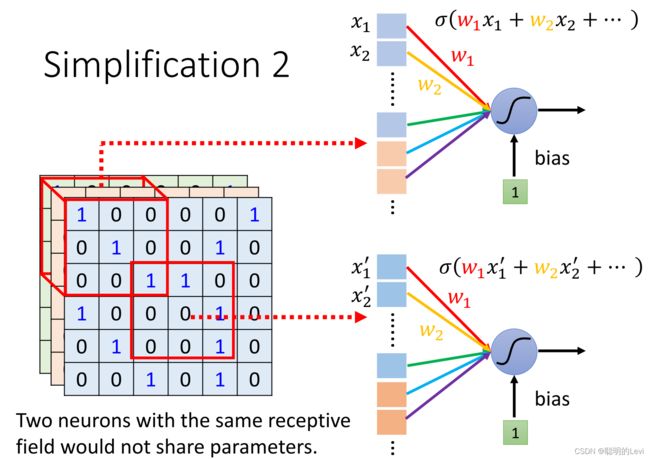
Simplification 2:采用parameter sharing
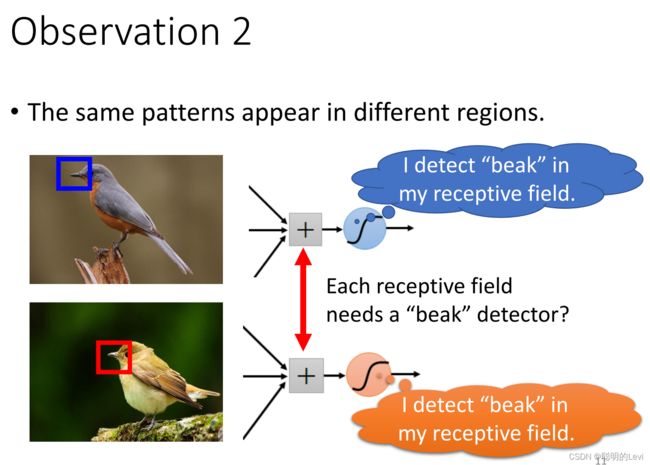
在侦测过程中,每一组neuron会用不同参数来侦测同一个pattern,如上图:p1会用该守备范围中的neuron的一个参数来侦测鸟喙,而p2会用自己守备范围的neuron中的另一个参数来侦测鸟喙。因此发现可以用同一个参数来侦测同一种pattern。
parameter sharing是基于simplification1的方法,也需要用到receptive field。
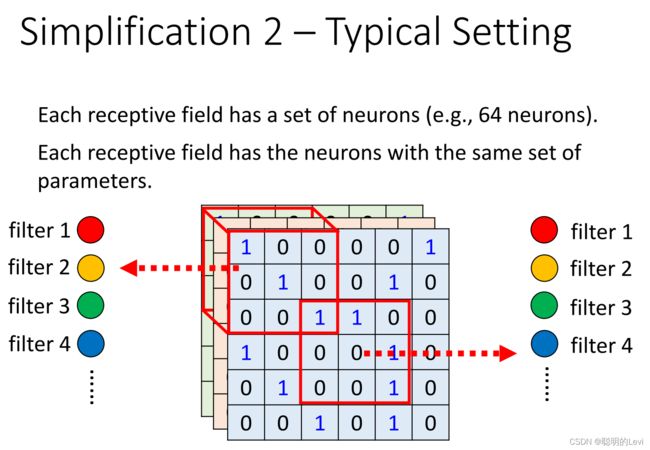
每一个receptive field都有一组neuron守备,一个黑圆代表一个neuron。

两个receptive field之间,它们中的两组neuron,相同颜色的neuron表示这两个neuron之间共享同一组参数。因此所有receptive field只有一组参数。共享同一组参数的neuron number称为filter number(number表示某数字序号)
Conclusion:
Fully Connected Layer:弹性最大
Receptive Field:不需要看整张图片,只需要看一个范围
parameter sharing:共享相同作用的参数

Explanation 2:Filter Version
filter的介绍
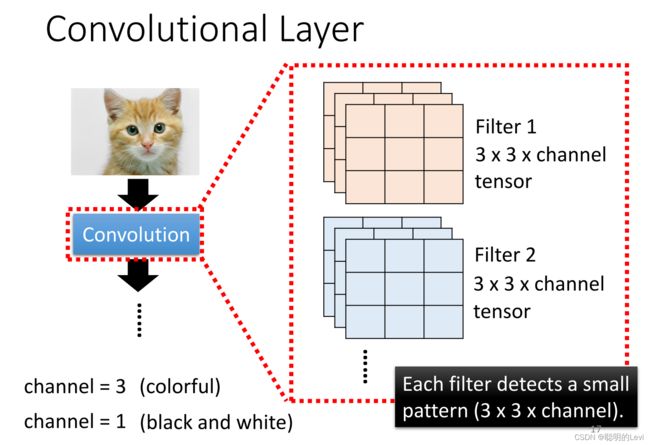
在第一层convolution中,有很多filter,filter的大小为3 x 3 x channel’s size(前两项也是自定义,不一定是3x3;若图片为彩色,则channel = 3,若为黑白,则channel = 1)。每一个filter都称为tensor。
filter如何与图片运作
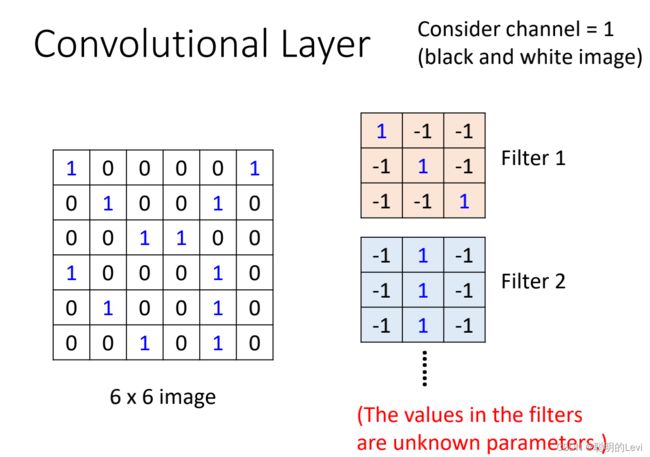
假设图片是黑白的。Filter的大小为3x3x1。这些filter中的参数来源于model中的parameter,是未知的,需要通过gradient descent计算出。在这里假设参数已经求出。
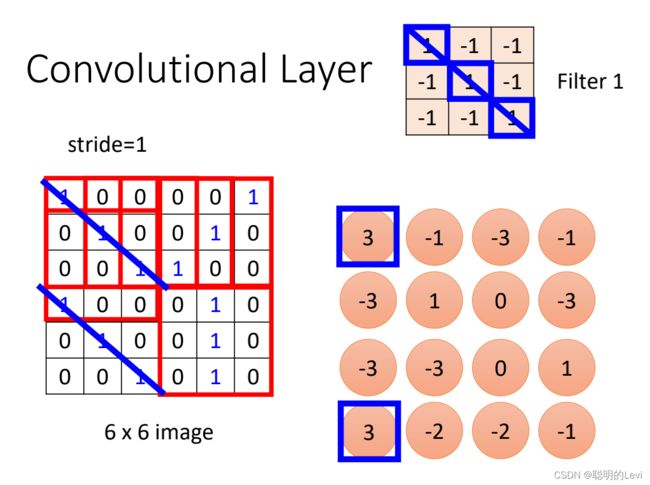
将filter与receptive field作interproduct(内积)。如上图中,filter 1与image中左上角的receptive field做interproduct,得到值3,并放在一个新的矩阵的左上角中。stride = 1,因此将field向右移动一个单位,新的field再次和filter 1做内积,得到值-1,置于矩阵中。重复上述操作,直至receptive field覆盖image。
filter与field做内积 = filter侦测pattern,是因为:做内积后,得到的数值越大证明该receptive field与filter越相似。在上图中,filter的对角线为1&1&1,在receptive field中对角线也是1&1&1时,内积得到的值最大。
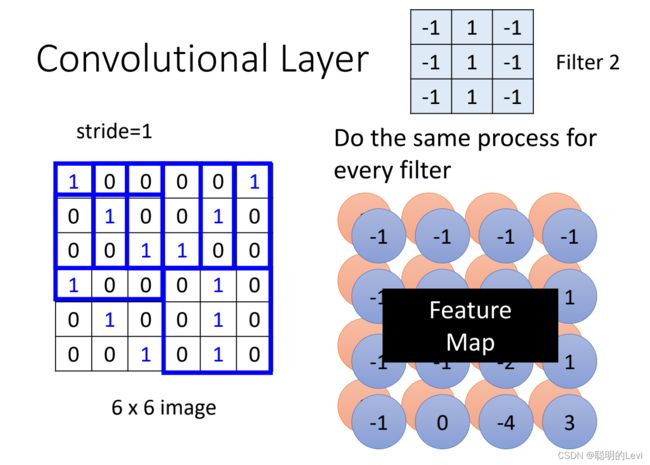
filter 2像上述一样做内积,再得到一群数字。假设共有64个filter,我们则会有64群数字。通过内积得到的所有数字,称为Feature Map。可以将feature map看作一张channel为64,size为4x4的新图片。
Multiple convolution layers
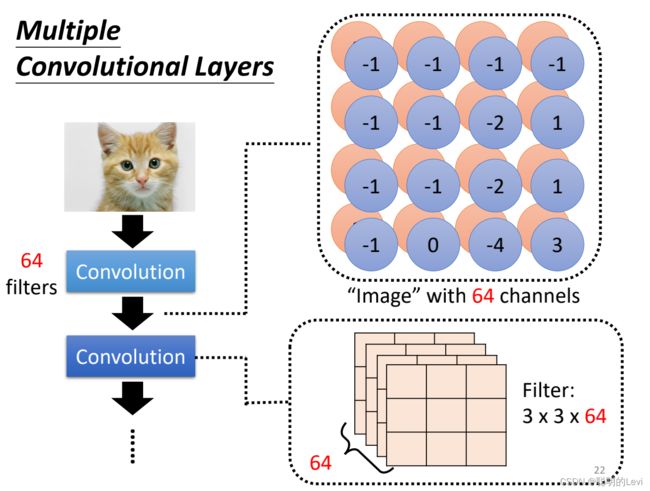
在第二层的convolution中,也有很多的filter,size为3x3,高度必须设为channel数目,即64。 第二层的channel数目为第一层convolutional layer的filter数目。
在第二层的convolution中,如下图所示:
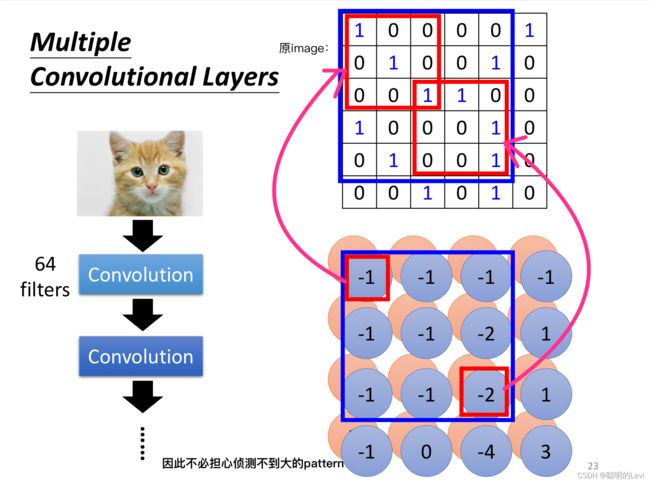
假设filter的size仍为3x3,第二层的convolutional layer中,蓝色框起来的部分:左上角的-1对应箭头所指范围,右下角的-2对应箭头所指范围,箭头所指的image为原image。如此在一次内积后,能侦测原image中5x5范围中的pattern。因此不必担心侦测不到图案大的pattern。
Comparison of two stories

Explanation 1中的共享参数,共有3x3x3个,对应到Explanation 2中的filter里3x3x3个参数。上图中,相同颜色表示参数一致。

Pooling
Pooling 是如何运作的
Pooling中不含参数,不需要学习,仅仅是一个Operator。Pooling有很多版本,下面讲述 Max pooling:
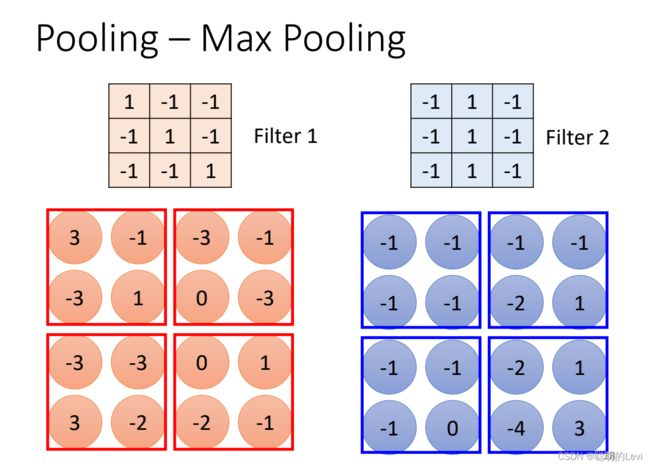
在Max Pooling中,filter得到的一群数字后,将数字分为n x n的square(n为自定义数字),选取每一个square中最大的数字作为每一个square的代表。图片通过pooling就能从4x4的图片变成2x2的图片。
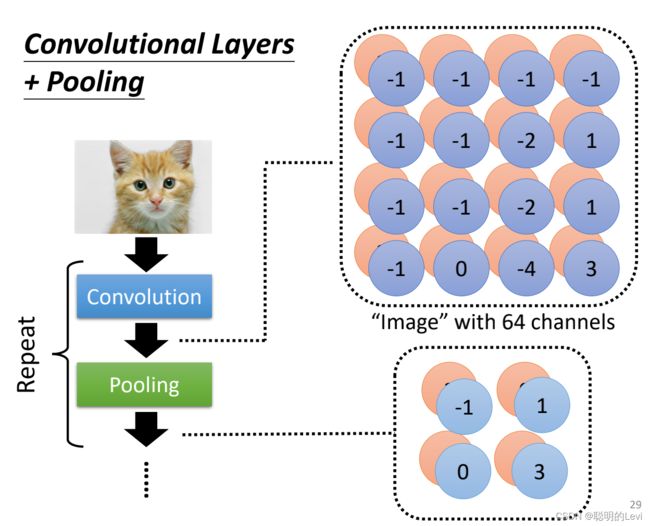 Convolution与pooling一般交替使用。需要注意的是:若需要在图片中侦测细微的东西,使用pooling则会降低侦测效果,使用pooling的原因是为了减少影像,从而减少运算量,因此pooling操作不是必要的。
Convolution与pooling一般交替使用。需要注意的是:若需要在图片中侦测细微的东西,使用pooling则会降低侦测效果,使用pooling的原因是为了减少影像,从而减少运算量,因此pooling操作不是必要的。

pooling后的操作是:将矩阵中的数值拉直成一个向量,再将该向量放入fully connected的layer中,再经过softmax得到最后的辨识结果。