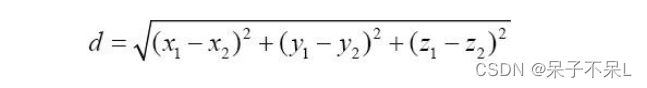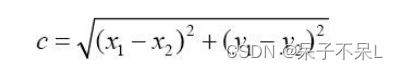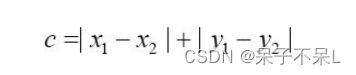机器学习入门 —— KNN 算法

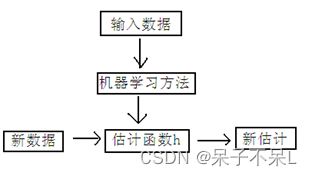
一、机器学习原理

 二、机器学习分类

如何进行电影分类

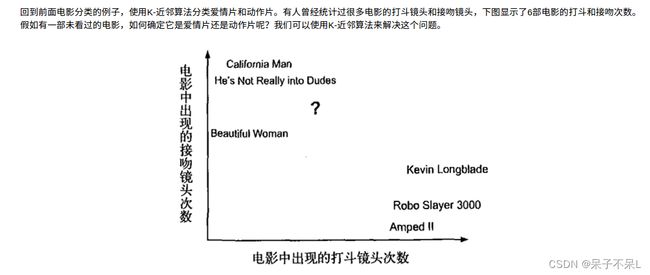
众所周知，电影可以按照题材分类，然而题材本身是如何定义的?由谁来判定某部电影属于哪 个题材?也就是说同一题材的电影具有哪些公共特征?这些都是在进行电影分类时必须要考虑的问 题。没有哪个电影人会说自己制作的电影和以前的某部电影类似，但我们确实知道每部电影在风格 上的确有可能会和同题材的电影相近。那么动作片具有哪些共有特征，使得动作片之间非常类似， 而与爱情片存在着明显的差别呢？动作片中也会存在接吻镜头，爱情片中也会存在打斗场景，我们 不能单纯依靠是否存在打斗或者亲吻来判断影片的类型。但是爱情片中的亲吻镜头更多，动作片中 的打斗场景也更频繁，基于此类场景在某部电影中出现的次数可以用来进行电影分类。

1.有监督学习

主要用于决策支持，它利用有标识的历史数据进行训练，以实现对新数据的表示的预测

1）分类

分类计数预测的数据对象是离散的。如短信是否为垃圾短信，用户是否喜欢电子产品

例如：K近邻、朴素贝叶斯、决策树、SVM

2）回归

回归技术预测的数据对象是连续值。例如温度变化或时间变化。包括一元回归和多元回归，线性回归和非线性回归

例如：线性回归、岭回归、Lasso回归

2.无监督学习

主要用于知识发现，在历史数据中发现隐藏的模式或内在结构

1）聚类

聚类算法用于在数据中寻找隐藏的模式或分组。

例如：K-means

3.半监督学习

在半监督学习方式下，训练数据有部分被标识，部分没有被标识，这种模型首先需要学习数据的内在结构，以便合理的组织数据来进行预测。算法上，包括一些对常用监督式学习算法的延伸，这些算法首先试图对未标识数据进行建模，在此基础上再对标识的数据进行预测。

例如：深度学习

三、k-近邻算法原理

如何进行电影分类

众所周知，电影可以按照题材分类，然而题材本身是如何定义的?由谁来判定某部电影属于哪 个题材?也就是说同一题材的电影具有哪些公共特征?这些都是在进行电影分类时必须要考虑的问 题。没有哪个电影人会说自己制作的电影和以前的某部电影类似，但我们确实知道每部电影在风格 上的确有可能会和同题材的电影相近。那么动作片具有哪些共有特征，使得动作片之间非常类似， 而与爱情片存在着明显的差别呢？动作片中也会存在接吻镜头，爱情片中也会存在打斗场景，我们 不能单纯依靠是否存在打斗或者亲吻来判断影片的类型。但是爱情片中的亲吻镜头更多，动作片中 的打斗场景也更频繁，基于此类场景在某部电影中出现的次数可以用来进行电影分类。

1.简单地说，K-近邻算法采用测量不同特征值之间的距离方法进行分类（k-Nearest Neighbor，KNN）

1）优点：精度高、对异常值不敏感、无数据输入假定。

2）缺点：时间复杂度高、空间复杂度高。

（1）当样本不平衡时，比如一个类的样本容量很大，其他类的样本容量很小，输入一个样本的时候，K个临近值中大多数都是大样本容量的那个类，这时可能就会导致分类错误。改进方法是对K临近点进行加权，也就是距离近的点的权值大，距离远的点权值小。 

（2）计算量较大，每个待分类的样本都要计算它到全部点的距离，根据距离排序才能求得K个临近点，改进方法是：先对已知样本点进行剪辑，事先去除对分类作用不大的样本。

3）适用数据范围：数值型和标称型

（1）标称型：标称型目标变量的结果只在有限目标集中取值，如真与假(标称型目标变量主要用于分类)

（2）数值型：数值型目标变量则可以从无限的数值集合中取值，如0.100，42.001等 (数值型目标变量主要用于回归分析)

2.工作原理

1）训练样本集

存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据 与所属分类的对应关系。输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的 特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签。一般来说，我们 只选择样本数据集中前K个最相似的数据，这就是K-近邻算法中K的出处,通常K是不大于20的整数。 最后 ，选择K个最相似数据中出现次数最多的分类，作为新数据的分类。

2）电影类别KNN分析

 3）欧几里得距离(Euclidean Distance)

        回想⼀下计算标准差的过程，“把每个学⽣每⻔课的成绩减去平均分，再把这些差值分别平⽅，将这 些平⽅的结果再加和，之后除以学⽣数量，最后开平⽅”。

        注意中间这个过程：“每⻔课程的成绩减去平均分，再把差值平⽅”，这其实就是在求“欧⽒距离”的 过程。

        所谓欧⽒距离中的“欧”指的是被称作⼏何之⽗的古希腊数学家欧⼏⾥得。欧⽒距离是在其巨著《⼏ 何原本》中提到的⼀个⾮常重要的概念。欧⽒距离的定义⼤概是这样的：在⼀个N维度的空间⾥，求 两个点的距离，这个距离肯定是⼀个⼤于等于0的数字（也就是说没有负距离，最⼩也就是两个点重 合的零距离），那么这个距离需要⽤两个点在各⾃维度上的坐标相减，平⽅后加和再开平⽅。

        欧⽒距离使⽤的范围实在是太⼴泛了，我们⼏乎每天都在使⽤。

        ⼀维的应⽤就相当多，如在地图上有⼀条笔直的东⻄向或者南北向的路，在上⾯有两个点，怎么量取 它们在地图上的距离？数轴标识如图4-12所示，可以⽤尺⼦的刻度贯穿两个点，⼤值减⼩值就能直 接得出结果，最多再乘以⼀个⽐例尺就能得到实际的⼤⼩。或者⽤其中⼀个点的读数减去另外⼀个点 的读数，不管结果正负，将它平⽅后再开⽅，还是⼀个⾮负数的值，这两种办法本质上没有什么区 别。地图明明是⼀个⼆维平⾯的概念，为什么⾮要说是⼀维的呢？只是因为量取的⼿段和⼀维⼀样， 只参考⼀个维度的读数就可以了。

⼆维的应⽤也是很多的，其中最典型的莫过于⼈们熟知的“勾股定理”。公式如下： 

 即：

        在⼀个直⻆三⻆形⾥，斜边⻓度等于两个直⻆边平⽅之和再开⽅。这其实就是求斜边两个端点的欧⽒ 距离，别忘了这⾥有⼀个隐含条件，就是斜边距离是不能⽤尺⼦直接去量的，只能⽤两个已知的直⻆ 边的⻓度做条件。⾄于斜边⻓度等于两个直⻆边之和的定理在不同的阶段⽤三⻆函数作为⼯具证明 过，⽤⾯积作为⼯具证明过，⽤相似三⻆形的⽅法证明过，⽅法实在是太多了，在百度⽹⻚搜索中我 们⾄少可以找到 16 种完全不同⽽且都是正确的⽅法。图 2 所示为⼀种⼆维空间中的向量计算⽅式示 意图，在知道向量分别在 x 轴和 y 轴的投影之后就能⽤勾股定理求出欧⽒距离。

        推⼴到三维的应⽤，还是可以使⽤勾股定理的思路进⾏计算。每个点都向3个平⾯各做⼀条垂线段， 可以看出，两个点的距离其实就是⼀个⻓⽅体的对⻆线⻓度。最后得到距离为 3 个维度的坐标差值 分别平⽅加和再开平⽅：

        这只是在两个平⾯空间中⽤了两次勾股定理⽽已。

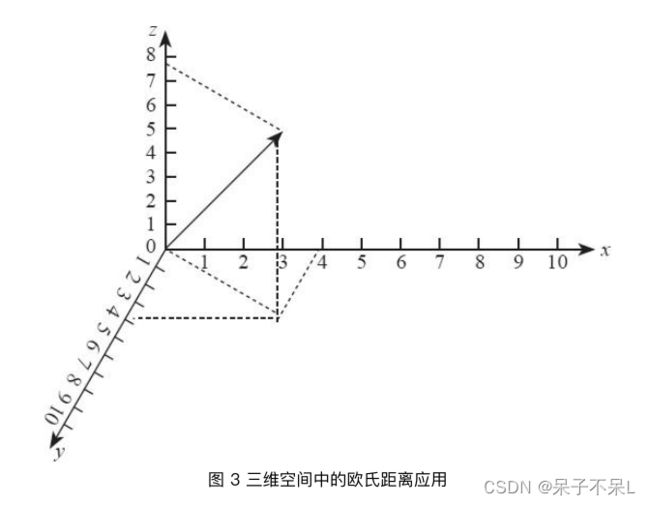
        例如，在忽略地球⾃身弧度的情况下，求两个距离较近的不同⾼度的楼宇顶部距离，完全可以使⽤这 种欧⽒距离的定义直接求解。如图 3 所示，在三维空间中，实际需要使⽤两次⼆维空间上的勾股定 理就能计算出三维空间中的两点之间的欧⽒距离。

 根据上述⼀维、⼆维、三维的欧⽒距离计算⽅法：

可以推断四维、五维⼀直到N维空间上的欧⽒距离的计算公式，⼀定是 N 个维度的“读数”差的平⽅ 再开⽅。

        欧⽒距离除了刚刚举的例⼦，在后⾯数据挖掘部分会有很多应⽤场景。它主要⽤来描述两个多维点之 间的“距离”，遗憾的是，三维以下的点和点的距离通过刚刚的讲解很容易出现画⾯感，四维和四维 以上的距离就只能凭想象了，只是在计算中确实存在且有对应的含义解释。这种解释通常也⽤来直接 判断两个点在多维关系上谁与谁更“近”，虽然超过三维的情况下这个“近”已经没有办法⽤⼿边的⼯ 具量出来。例如，在⼀个五维空间⾥，A 点和 B 点的距离为 6，A 点和 C 点的距离为 10，那么就可 以认为 B 点到 A 点的距离⽐ C 点到 A 点的距离更近，这样就⾜够了。

4）计算过程图

四、曼哈顿距离算法

        欧⽒距离是⼈们在解析⼏何⾥最常⽤的⼀种计算⽅法，但是计算起来⽐较复杂，要平⽅，加和，再开 ⽅，⽽⼈们在空间⼏何中度量距离很多场合其实是可以做⼀些简化的。曼哈顿距离就是由 19 世纪著 名的德国犹太⼈数学家赫尔曼·闵可夫斯基发明的。

        赫尔曼·闵可夫斯基在少年时期就在数学⽅⾯表现出极⾼的天分，他是后来四维时空理论的创⽴者， 也曾经是著名物理学家爱因斯坦的⽼师。

        曼哈顿距离也叫出租⻋距离，⽤来标明两个点在标准坐标系上的绝对轴距总和。简单来说，对⽐⼀下 欧⽒距离。

欧⽒距离⾥的距离计算：

 曼哈顿距离中的距离计算：

        曼哈顿距离中的距离计算公式⽐欧⽒距离的计算公式看起来简洁很多，只需要把两个点坐标的 x 坐 标相减取绝对值，y 坐标相减取绝对值，再加和。

        从公式定义上看，曼哈顿距离⼀定是⼀个⾮负数，距离最⼩的情况就是两个点重合，距离为 0，这⼀ 点和欧⽒距离⼀样。曼哈顿距离和欧⽒距离的意义相近，也是为了描述两个点之间的距离，不同的是 曼哈顿距离只需要做加减法，这使得计算机在⼤量的计算过程中代价更低，⽽且会消除在开平⽅过程 中取近似值⽽带来的误差。不仅如此，曼哈顿距离在⼈脱离计算机做计算的时候也会很⽅便。

        之所以曼哈顿距离⼜被称为出租⻋距离是因为在像纽约曼哈顿区这样的地区有很多由横平竖直的街道 所切成的街区（Block），出租⻋司机计算从⼀个位置到另⼀个位置的距离，通常直接⽤街区的两个 坐标分别相减，再相加，这个结果就是他即将开⻋通过的街区数量，⽽完全没有必要⽤欧⽒距离来求 解——算起来超级麻烦还没有意义，毕竟谁也没办法从欧⽒距离的直线上⻜过去。如图 3 所示，假 设⼀辆出租⻋要从上⾯的圆圈位置⾛到下⾯的圆圈位置，⽆论是左边的线路，还是右边的线路，都要 经过 11 个街区，⽽这个 11 就是曼哈顿距离。

        从曼哈顿距离的定义就能看出，曼哈顿距离的创⽴，与其说有很⼤的学术意义不如说更多的是应⽤意 义。这也是本书⼀直想说的⼀点，数学就在我们身边，它是我们的⼯具，能帮我们解决问题⽽不是带 来麻烦。

 上⾯的公式只给了⼆维空间上的曼哈顿距离公式，三维、四维或者更多维度的计算原理是⼀样。