基于阿基米德优化算法的函数寻优算法
文章目录
- 一、理论基础
-
- 1、算法步骤
-
- (1)初始化
- (2)更新密度和体积
- (3)转移算子与密度算子
- (4)勘探阶段
-
- <1> 物体之间发生碰撞
- <2> 物体之间无碰撞
- <3> 标准化加速度
- (5)位置更新
- (6)适应度函数
- 2、算法伪代码
- 二、仿真实验与分析
- 三、参考文献
一、理论基础
阿基米德优化算法( Archimedes optimization algorithm, AOA)是一种基于群体的启发式算法。在该方法中,种群个体是沉浸对象。与其他基于种群的元启发式算法一样,AOA也从具有随机体积、密度和加速度的初始种群(候选解)开始搜索过程。在这个阶段,每个对象也用它在流体中的随机位置初始化。在评估初始种群的适应度后,AOA进行迭代直到满足终止条件。在每次迭代中,AOA都会更新每个对象的密度和体积。根据物体与相邻物体碰撞的情况,更新物体的加速度。更新后的密度、体积、加速度决定了物体的新位置。下面是AOA步骤的详细数学表达式。
1、算法步骤
(1)初始化
利用公式(1)初始化所有物体的位置: O i = l b i + r a n d × ( u b i − l b i ) ; i = 1 , 2 , ⋯ , N (1) O_i=lb_i+rand×(ub_i-lb_i);i=1,2,\cdots,N\tag{1} Oi=lbi+rand×(ubi−lbi);i=1,2,⋯,N(1)其中, O i O_i Oi是 N N N个个体中的第 i i i个物体的位置; l b i lb_i lbi和 u b i ub_i ubi分别是搜索空间的下限和上限。
使用公式(2)初始化第 i i i个物体的体积( v o l vol vol)和密度( d e n den den): d e n i = r a n d v o l i = r a n d (2) \begin{aligned}den_i &=rand\\vol_i &=rand\end{aligned}\tag{2} denivoli=rand=rand(2)其中, r a n d rand rand是一个在 [ 0 , 1 ] [0,1] [0,1]之间随机生成的 D D D维向量。
最后,使用公式(3)初始化物体的加速度( a c c acc acc): a c c i = l b i + r a n d × ( u b i − l b i ) (3) acc_i=lb_i+rand×(ub_i-lb_i)\tag{3} acci=lbi+rand×(ubi−lbi)(3)在此步骤中,评价初始总体并选择具有最佳适应度值的物体。分配 x b e s t x_{best} xbest、 d e n b e s t den_{best} denbest、 v o l b e s t vol_{best} volbest和 a c c b e s t acc_{best} accbest。
(2)更新密度和体积
第 t + 1 t+1 t+1次迭代的第 i i i个物体的密度和体积使用公式(4)更新: d e n i t + 1 = d e n i t + r a n d × ( d e n b e s t − d e n i t ) v o l i t + 1 = v o l i t + r a n d × ( v o l b e s t − v o l i t ) (4) \begin{aligned}den_i^{t+1} &=den_i^t+rand×(den_{best}-den_i^t)\\vol_i^{t+1} &=vol_i^t+rand×(vol_{best}-vol_i^t)\end{aligned}\tag{4} denit+1volit+1=denit+rand×(denbest−denit)=volit+rand×(volbest−volit)(4)其中, d e n b e s t den_{best} denbest和 v o l b e s t vol_{best} volbest是到目前为止发现的物体的最好密度和体积; r a n d rand rand是 [ 0 , 1 ] [0,1] [0,1]间的随机数。
(3)转移算子与密度算子
起初,物体之间发生碰撞,经过一段时间后,物体试图达到平衡状态。这是在AOA中通过转移运算符 T F TF TF实现的, T F TF TF将搜索从勘探转换为开发,使用公式(5)定义: T F = exp ( t − t m a x t m a x ) (5) TF=\exp(\frac{t-t_{max}}{t_{max}})\tag{5} TF=exp(tmaxt−tmax)(5)其中,随着时间的推移,转移因子逐渐增加,直至达到1; t t t和 t m a x t_{max} tmax分别表示当前迭代次数和最大迭代次数。类似地,密度递减因子 d d d也有助于AOA从全局到局部的搜索,它使用公式(6)随着时间的推移而减少: d t + 1 = exp ( t m a x − t t m a x ) − ( t t m a x ) (6) d^{t+1}=\exp\left(\frac{t_{max}-t}{t_{max}}\right)-\left(\frac{t}{t_{max}}\right)\tag{6} dt+1=exp(tmaxtmax−t)−(tmaxt)(6) d t + 1 d^{t+1} dt+1随着迭代次数的增大而减小,这使得它能够在已经确定的有希望的区域内收敛。请注意,正确处理此变量将确保AOA中勘探和开采之间的平衡。
(4)勘探阶段
<1> 物体之间发生碰撞
如果 T F ≤ 0.5 TF≤0.5 TF≤0.5,物体之间发生碰撞,随机选择一个物体( m r mr mr)并使用公式(7)更新 t + 1 t+1 t+1次迭代物体加速度: a c c i t + 1 = d e n m r + v o l m r × a c c m r d e n i t + 1 × v o l i t + 1 (7) acc_i^{t+1}=\frac{den_{mr}+vol_{mr}×acc_{mr}}{den_i^{t+1}×vol_i^{t+1}}\tag{7} accit+1=denit+1×volit+1denmr+volmr×accmr(7)其中, d e n i , v o l i den_i,vol_i deni,voli和 a c c i acc_i acci分别是物体 i i i的密度、体积和加速度; a c c m r , d e n m r acc_{mr},den_{mr} accmr,denmr和 v o l m r vol_{mr} volmr是随机物体的加速度、密度和体积。值得一提的是, T F ≤ 0.5 TF≤0.5 TF≤0.5可确保在三分之一的迭代中进行探索。应用0.5以外的值将改变勘探开发行为。
<2> 物体之间无碰撞
如果 T F > 0.5 TF>0.5 TF>0.5,物体之间无碰撞,使用公式(8)更新 t + 1 t+1 t+1次迭代物体加速度: a c c i t + 1 = d e n b e s t + v o l b e s t × a c c b e s t d e n i t + 1 × v o l i t + 1 (8) acc_i^{t+1}=\frac{den_{best}+vol_{best}×acc_{best}}{den_i^{t+1}×vol_i^{t+1}}\tag{8} accit+1=denit+1×volit+1denbest+volbest×accbest(8)其中, a c c b e s t acc_{best} accbest是物体的最优加速度。
<3> 标准化加速度
使用公式(9)标准化加速度以计算变化百分比: a c c i − n o r m t + 1 = u × a c c i t + 1 − min ( a c c ) max ( a c c ) − min ( a c c ) + l (9) acc_{i-norm}^{t+1}=u×\frac{acc_i^{t+1}-\min(acc)}{\max(acc)-\min(acc)}+l\tag{9} acci−normt+1=u×max(acc)−min(acc)accit+1−min(acc)+l(9)其中, u u u和 l l l是归一化范围,分别设置为0.9和0.1。 a c c i − n o r m t + 1 acc_{i-norm}^{t+1} acci−normt+1i决定每个代理将更改的步长百分比。如果目标 i i i远离全局最优值,则加速度值将很高,这意味着目标将处于勘探阶段;否则,将处于开发阶段。这说明了搜索是如何从探索阶段转变为开发阶段的。在正常情况下,加速度因子从大值开始,随时间减小。这有助于搜索代理朝着全球最佳解决方案的方向发展,同时他们也远离了本地解决方案。但是,值得一提的是,可能仍然有一些搜索代理需要更多的时间停留在探索阶段比正常情况下。因此,AOA实现了勘探与开发的平衡。
(5)位置更新
如果 T F ≤ 0.5 TF≤0.5 TF≤0.5(勘探阶段),则使用公式(10)计算第 t + 1 t+1 t+1代时第 i i i个物体的位置: x i t + 1 = x i t + C 1 × r a n d × a c c i − n o r m t + 1 × d × ( x r a n d − x i t ) (10) x_i^{t+1}=x_i^t+C_1×rand×acc_{i-norm}^{t+1}×d×(x_{rand}-x_i^t)\tag{10} xit+1=xit+C1×rand×acci−normt+1×d×(xrand−xit)(10)其中, C 1 = 2 C_1=2 C1=2。否则,如果 T F > 0.5 TF>0.5 TF>0.5(开发阶段),物体将使用公式(11)更新其位置。 x i t + 1 = x b e s t t + F × C 2 × r a n d × a c c i − n o r m t + 1 × d × ( T × x b e s t − x i t ) (11) x_i^{t+1}=x_{best}^t+F×C_2×rand×acc_{i-norm}^{t+1}×d×(T×x_{best}-x_i^t)\tag{11} xit+1=xbestt+F×C2×rand×acci−normt+1×d×(T×xbest−xit)(11)其中, C 2 = 6 C_2=6 C2=6; T T T随迭代次数增加,与转移算子成正比,用 T = C 3 × T F T=C3×TF T=C3×TF定义。在 [ C 3 × 0.3 , 1 ] [C3×0.3,1] [C3×0.3,1]范围内, T T T随迭代增加,并从最佳位置开始有一定的百分比。它以较低的百分比开始,因为这会导致最佳位置和当前位置之间的较大差异,因此随机游动的步长将很高。随着搜索的进行,该百分比逐渐增加,以减小最佳位置和当前位置之间的差异。这导致在勘探和开发之间实现适当的平衡。
F F F是使用公式(12)改变运动方向的标志: F = { + 1 if P ≤ 0.5 − 1 if P > 0.5 (12) F=\begin{dcases}+1\quad \text{if}\,\,P≤0.5\\-1\quad\text{if}\,\,P>0.5\end{dcases}\tag{12} F={+1ifP≤0.5−1ifP>0.5(12)其中, P = 2 × r a n d − C 4 P=2×rand-C_4 P=2×rand−C4。
(6)适应度函数
使用目标函数 f f f评价每个物体,并记住迄今为止找到的最优解。分配 x b e s t x_{best} xbest、 d e n b e s t den_{best} denbest、 v o l b e s t vol_{best} volbest和 a c c b e s t acc_{best} accbest。
2、算法伪代码
注:伪代码里面的公式编号与文献[1]一致。
二、仿真实验与分析
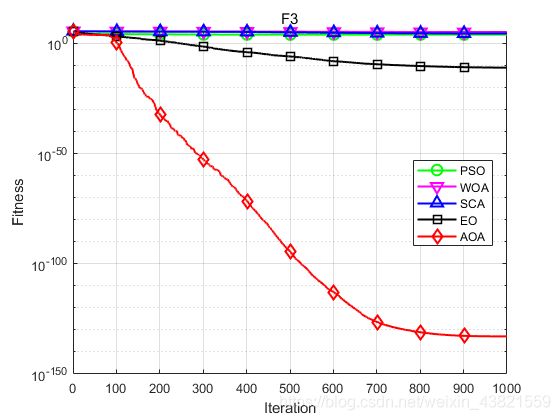
AOA与PSO、WOA、SCA、EO[2]进行对比,具体的算法参数如文献[1]所示。种群规模 N = 30 N=30 N=30,最大迭代次数 t m a x = 1000 t_{max}=1000 tmax=1000,独立运算30次,取平均值,函数维度为50,以F1~F3为例。结果显示如下:
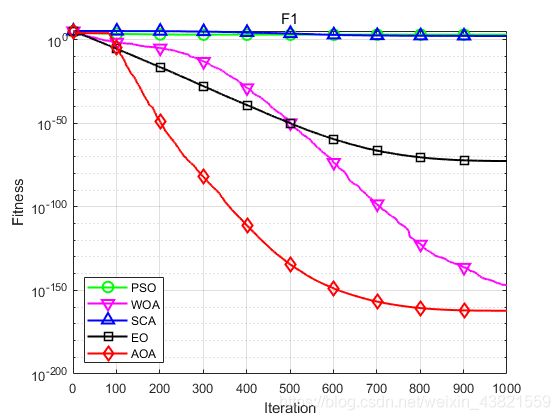

函数:F1
PSO:最大值: 1485.54,最小值:347.6035,平均值:784.0037,标准差:280.1856
WOA:最大值: 3.1261e-146,最小值:1.6652e-166,平均值:1.0422e-147,标准差:5.7074e-147
SCA:最大值: 1153.2582,最小值:0.018977,平均值:136.5338,标准差:241.297
EO:最大值: 4.2721e-72,最小值:5.3103e-77,平均值:2.255e-73,标准差:7.8124e-73
AOA:最大值: 2.1005e-161,最小值:1.8845e-228,平均值:7.0278e-163,标准差:3.8499e-162
函数:F2
PSO:最大值: 38.1003,最小值:15.7591,平均值:26.5815,标准差:5.7641
WOA:最大值: 8.5664e-101,最小值:3.5978e-112,平均值:2.8665e-102,标准差:1.5638e-101
SCA:最大值: 0.13066,最小值:5.3512e-05,平均值:0.015445,标准差:0.02847
EO:最大值: 1.4203e-41,最小值:5.041e-44,平均值:2.6473e-42,标准差:3.4168e-42
AOA:最大值: 2.551e-85,最小值:6.9849e-122,平均值:9.9267e-87,标准差:4.6923e-86
函数:F3
PSO:最大值: 30029.6602,最小值:5472.2506,平均值:10728.4495,标准差:4679.599
WOA:最大值: 173941.083,最小值:31689.8106,平均值:128923.5682,标准差:29537.5037
SCA:最大值: 72856.2459,最小值:13323.4109,平均值:33375.0035,标准差:12860.808
EO:最大值: 1.102e-10,最小值:5.399e-17,平均值:1.0833e-11,标准差:2.7705e-11
AOA:最大值: 3.6676e-132,最小值:3.7115e-199,平均值:1.2226e-133,标准差:6.6961e-133
由此可见,AOA算法比其他智能算法的寻优精度更高、求解效果更好。
三、参考文献
[1] Hashim, F.A., Hussain, K., Houssein, E.H. et al. Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems[J]. Applied Intelligence, 2021, 51: 1531-1551.
[2] Afshin Faramarzi, Mohammad Heidarinejad, Brent Stephens, Seyedali Mirjalili. Equilibrium optimizer: A novel optimization algorithm[J]. Knowledge-Based Systems, 2020, 191: 105190.
