机器学习实战教程(二):决策树基础篇(构建决策树1决策树的构建2信息增益3任务需求4ID3信息增益条件熵计算信息增益5.递归构建决策树递归构建决策树代码6C4.5信息增益率7CATRGini系)
文章目录
- 构建决策树
-
- 1.决策树的构建
- 2.信息增益
- 3.任务需求
- 4.ID3 信息增益
-
- 条件熵
- 计算信息增益
- 5.递归构建决策树
-
- 递归构建决策树代码
- 6 C4.5:信息增益率
- 7 CATR: Gini系数
- 8 过拟合与剪枝
-
- 过拟合 Overfitting
- 9 决策树算法种类
- 10 决策树鸢尾花实战
-
- 案例一
- 案例二
-
- 决策树可视化环境搭建
- 案例三
构建决策树
1.决策树的构建
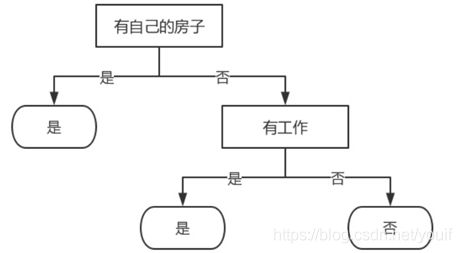
构造决策树,随着深度的增加,节点的熵迅速降低。熵降低的速度越快越好,迅速地构建出决策树,希望得到一颗高度最矮的决策树。
使用决策树做预测的每一步骤都很重要,数据收集不到位,将会导致没有足够的特征让我们构建错误率低的决策树。数据特征充足,但是不知道用哪些特征好,将会导致无法构建出分类效果好的决策树模型。从算法方面看,决策树的构建是我们的核心内容,主要就是节点的选择。

注意到树的内部结点就是属性,现在问题是。怎样决定用哪一个属性做根节点。
只要建立了决策树,预测的过程是很简单的。关键是怎么根据训练集建立决策树。

2.信息增益
特征选择在于选取对训练数据具有分类能力的特征。这样可以提高决策树学习的效率,如果利用一个特征进行分类的结果与随机分类的结果没有很大差别,则称这个特征是没有分类能力的。经验上扔掉这样的特征对决策树学习的精度影响不大。通常特征选择的标准是信息增益(information gain)或信息增益比。
如果一个特征具有更好的分类能力,或者说按照这一特征将训练数据集分割成子集,使得各个子集在当前条件下有最好的分类,那么就更应该选择这个特征.信息增益(information gain)就能够很好地表示这一直观的准则。
有自己的房子会对银行贷款带来约束,这个约束到底有多大,其实就是信息增益。
3.任务需求
希望通过所给的训练数据学习一个贷款申请的决策树,用于对未来的贷款申请进行分类,即当新的客户提出贷款申请时,根据申请人的特征利用决策树决定是否批准贷款申请。
银行在不知道你的情况下,是随机给你贷款的,100个人的话,随机 ,熵就会非常的大。年龄与类别的信息增益多大,工作与类别信息增益多大等等,分别算出信息增益,每个特征对类别的约束作用是不一样的,这就是决策树分类的依据。
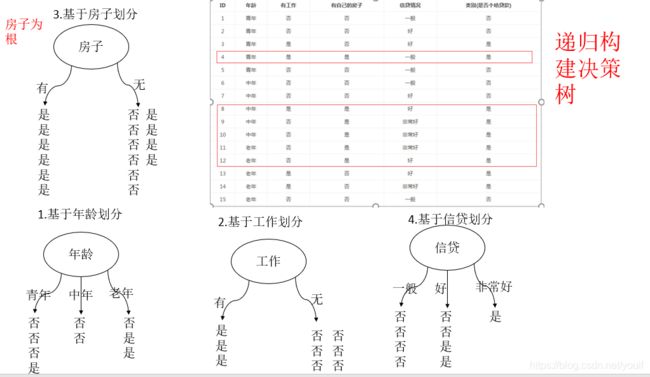
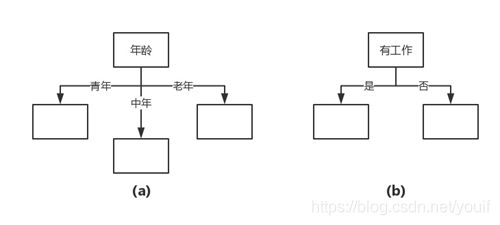
划分特征空间。比如,我们通过上述数据表得到两个可能的决策树,分别由两个不同特征的根结点构成。

图(a)所示的根结点的特征是年龄,有3个取值,对应于不同的取值有不同的子结点。图(b)所示的根节点的特征是工作,有2个取值,对应于不同的取值有不同的子结点。两个决策树都可以从此延续下去。问题是:究竟选择哪个特征更好些?这就要求确定选择特征的准则。直观上,如果一个特征具有更好的分类能力,或者说,按照这一特征将训练数据集分割成子集,使得各个子集在当前条件下有最好的分类,那么就更应该选择这个特征。信息增益就能够很好地表示这一直观的准则。
4.ID3 信息增益
信息增益是相对于特征而言的,信息增益越大,特征对最终的分类结果影响也就越大,我们就应该选择对最终分类结果影响最大的那个特征作为我们的分类特征。
在讲解信息增益定义之前,我们还需要明确一个概念,条件熵。
熵我们知道是什么,条件熵又是个什么?
条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性,随机变量X给定的条件下随机变量Y的条件熵(conditional entropy)H(Y|X),定义为X给定条件下Y的条件概率分布的熵对X的数学期望:

条件熵
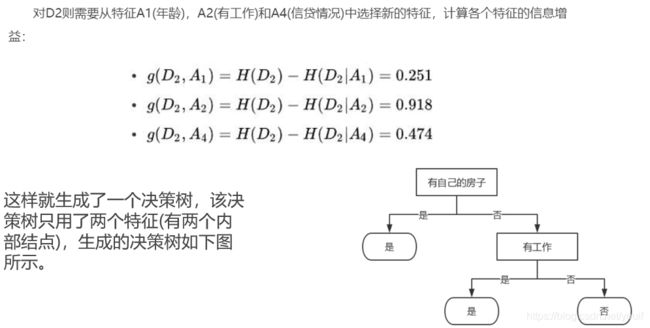
明确了条件熵和经验条件熵的概念。接下来,让我们说说信息增益。前面也提到了,信息增益是相对于特征而言的。所以,特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差,即:
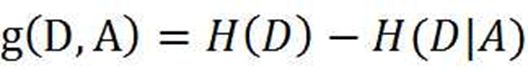
D是标签对应的列向量,A是其中的某一列特征,g是信息增益,从公式来理解更容易: 信息增益越大,特征对最终的分类结果影响也就越大?为何g要越大越好:类标签列信息 熵H (D)是固定值,g要大, 说明条件熵H(D|A)要小,条件熵意思是在已知A的情况 下,对于类标签列带来了多少约束,假设在确定A的情况下,类标签列只有一个取值(此时 D的条件熵最小),信息类似于直线向量,说明这个约束非常大,H(D|A)达到最小, 同 时也可以明显看出,这个特征对分类很有用,只要使用了该特征,就可以将类别全部分开, 此次我们说,这个特征对分类贡献最大,那么其信息增益也是最大的。
离散时:设特征A有n个不同的取值{a1,a2,···,an},根据特征A的取值将D划分为n个子集{D1,D2,···,Dn},|Di|为Di的样本个数。记子集Di中属于Ck的样本的集合为Dik,即Dik = Di ∩ Ck,|Dik|为Dik的样本个数。于是经验条件熵的公式可以些为:
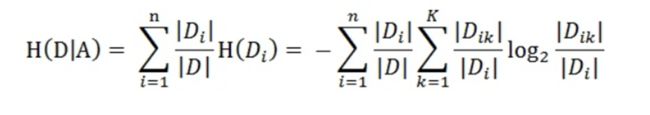
举几个例子,再回来看一下概念,就懂了
一共有三个类别,分别是:青年、中年和老年。我们只看年龄是青年的数据,年龄是青年的数据一共有5个,所以年龄是青年的数据在训练数据集出现的概率是十五分之五,也就是三分之一。同理,年龄是中年和老年的数据在训练数据集出现的概率也都是三分之一。现在我们只看年龄是青年的数据的最终得到贷款的概率为五分之二,因为在五个数据中,只有两个数据显示拿到了最终的贷款,同理,年龄是中年和老年的数据最终得到贷款的概率分别为五分之三、五分之四。所以计算年龄的信息增益,过程如下:

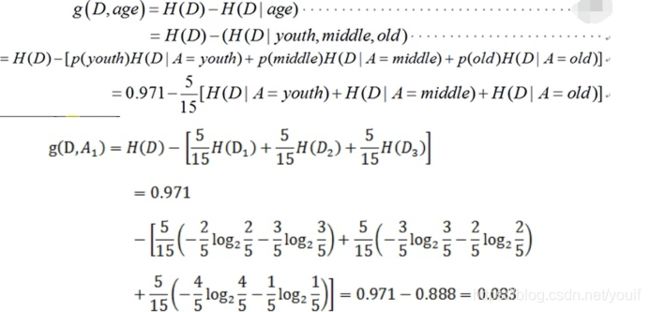


计算信息增益
# * coding:utf-8_*_
# 作者 :XiangLin
# 创建时间 :03/03/2020 21:05
# 文件 :informationgain.py
# IDE :PyCharm
from math import log
# from sklearn.tree import DecisionTreeClassifier
# from sklearn.cro
def createDataSet():
dataSet = [[0, 0, 0, 0, 'no'], # 数据集
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels = ['不放贷', '放贷'] # 分类属性
return dataSet, labels # 返回数据集和分类属性
'''
函数说明:计算给定数据集的经验熵(香农熵)
Parameters:
dataSet - 数据集
Returns:
shannonEnt - 经验熵(香农熵)
'''
def calcShannonEnt(dataSet):
numEntires = len(dataSet) # 返回数据集的行数
labelCounts = {} # 保存每个标签(Label)出现次数的字典
for featVec in dataSet: # 对每组特征向量进行统计
currentLable = featVec[-1] # 提取标签(Label)信息
if currentLable not in labelCounts.keys(): # 如果标签(Label)没有放入统计次数的字典,添加进去
labelCounts[currentLable] = 0
labelCounts[currentLable] += 1
shannonEnt = 0.0 # 经验熵(香农熵)
for key in labelCounts: # 计算香农熵
prob = float(labelCounts[key]) / numEntires # 选择该标签(Label)的概率
shannonEnt -= prob * log(prob, 2) # 利用公式计算
return shannonEnt # 返回经验熵(香农熵)
'''
函数说明:按照给定特征划分数据集
Parameters:
dataSet - 待划分的数据集
axis - 划分数据集的特征
value - 需要返回的特征的值
Returns:
无
'''
'''
dataSet = [[0, 0, 0, 0, 'no'], # 数据集
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
例如axis = 0,value = 0
[[0, 0, 0, 'no'],
[0, 0, 1, 'no'],
[1, 0, 1, 'yes'],
[1, 1, 0, 'yes'],
[0, 0, 0, 'no']]
'''
def splitDataSet(dataSet, axis, value):
retDataSet = [] #创建返回的数据集列表
for featVec in dataSet: #遍历数据集
if featVec[axis] == value:
reducedFeatVec = featVec[:axis] #去掉axis特征
# print('------')
# print(reducedFeatVec)
# reducedFeatVec = []
reducedFeatVec.extend(featVec[axis+1:]) #将符合条件的添加到返回的数据集
retDataSet.append(reducedFeatVec)
return retDataSet # 返回划分后的数据集
'''
函数说明:选择最优特征
Parameters:
dataSet - 数据集
Returns:
bestFeature - 信息增益最大的(最优)特征的索引值
'''
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 #特征数量
baseEntropy = calcShannonEnt(dataSet) #计算数据集的香农熵
bestInfoGain = 0.0 #信息增益
bestFeature = -1 #最优特征的索引值
for i in range(numFeatures): #遍历所有特征 一列一列遍历
# 获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet] #一列一列取 然后取一列中的i行 python的强大之处
print(featList)
uniqueValas = set(featList) #创建set集合{},元素不可重复
newEntropy = 0.0 #经验条件熵
for value in uniqueValas:
subDataSet = splitDataSet(dataSet,i,value) #subDataSet划分后的子集
print(subDataSet)
prob = len(subDataSet) / float(len(dataSet)) #计算子集的概率
newEntropy += prob * calcShannonEnt(subDataSet) #根据公式计算经验条件熵
infoGain = baseEntropy - newEntropy #信息增益
print("第%d个特征的增益为%.3f" % (i, infoGain))
if (infoGain > bestInfoGain): # 计算信息增益
bestInfoGain = infoGain # 更新信息增益,找到最大的信息增益
bestFeature = i #记录信息增益最大的特征的索引值
return bestFeature #返回信息增益最大的特征的索引值
if __name__ == '__main__':
dataSet, labels = createDataSet()
# print(dataSet)
# print(calcShannonEnt(dataSet))
print("最优特征索引值:" + str(chooseBestFeatureToSplit(dataSet)))
5.递归构建决策树
递归构建决策树代码
# * coding:utf-8_*_
# 作者 :XiangLin
# 创建时间 :04/03/2020 17:05
# 文件 :Decision.py
# IDE :PyCharm
from math import log
import pydotplus
def createDataSet():
dataSet = [[0, 0, 0, 0, 'no'], #数据集
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels = ['年龄', '有工作', '有自己的房子', '信贷情况'] #特征标签
return dataSet, labels #返回数据集和分类属性
'''
函数说明:计算给定数据集的经验熵(香农熵)
Parameters:
dataSet - 数据集
Returns:
shannonEnt - 经验熵(香农熵)
'''
def calcShannonEnt(dataSet):
numEntires = len(dataSet) # 返回数据集的行数
labelCounts = {} # 保存每个标签(Label)出现次数的字典
for featVec in dataSet: # 对每组特征向量进行统计
currentLable = featVec[-1] # 提取标签(Label)信息
if currentLable not in labelCounts.keys(): # 如果标签(Label)没有放入统计次数的字典,添加进去
labelCounts[currentLable] = 0
labelCounts[currentLable] += 1
shannonEnt = 0.0 # 经验熵(香农熵)
for key in labelCounts: # 计算香农熵
prob = float(labelCounts[key]) / numEntires # 选择该标签(Label)的概率
shannonEnt -= prob * log(prob, 2) # 利用公式计算
return shannonEnt # 返回经验熵(香农熵)
'''
函数说明:按照给定特征划分数据集
Parameters:
dataSet - 待划分的数据集
axis - 划分数据集的特征
value - 需要返回的特征的值
Returns:
无
'''
def splitDataSet(dataSet, axis, value):
retDataSet = [] #创建返回的数据集列表
for featVec in dataSet: #遍历数据集
if featVec[axis] == value:
reducedFeatVec = featVec[:axis] #去掉axis特征
reducedFeatVec.extend(featVec[axis+1:]) #将符合条件的添加到返回的数据集
retDataSet.append(reducedFeatVec)
return retDataSet
'''
函数说明:选择最优特征
Parameters:
dataSet - 数据集
Returns:
bestFeature - 信息增益最大的(最优)特征的索引值
'''
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 #特征数量
baseEntropy = calcShannonEnt(dataSet) #计算数据集的香农熵
bestInfoGain = 0.0 #信息增益
bestFeature = -1 #最优特征的索引值
for i in range(numFeatures): #遍历所有特征
#获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet]
uniqueVals = set(featList) #创建set集合{},元素不可重复
newEntropy = 0.0 #经验条件熵
for value in uniqueVals: #计算信息增益
subDataSet = splitDataSet(dataSet, i, value) #subDataSet划分后的子集
prob = len(subDataSet) / float(len(dataSet)) #计算子集的概率
newEntropy += prob * calcShannonEnt(subDataSet) #根据公式计算经验条件熵
infoGain = baseEntropy - newEntropy #信息增益
# print("第%d个特征的增益为%.3f" % (i, infoGain)) #打印每个特征的信息增益
if (infoGain > bestInfoGain): #计算信息增益
bestInfoGain = infoGain #更新信息增益,找到最大的信息增益
bestFeature = i #记录信息增益最大的特征的索引值
return bestFeature
'''
函数说明:统计classList中出现此处最多的元素(类标签)
Parameters:
classList - 类标签列表
Returns:
sortedClassCount[0][0] - 出现此处最多的元素(类标签)
'''
def majorityCnt(classList):
classCount = {}
for vote in classList: # 统计classList中每个元素出现的次数
if vote not in classCount.keys(): classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) # 根据字典的值降序排序
return sortedClassCount[0][0] # 返回classList中出现次数最多的元素
'''
函数说明:创建决策树
Parameters:
dataSet - 训练数据集
labels - 分类属性标签
featLabels - 存储选择的最优特征标签
Returns:
myTree - 决策树
'''
def createTree(dataSet, labels, featLabels):
classList = [example[-1] for example in dataSet] #取分类标签(是否放贷:yes or no)
# print(classList[0])
# print(classList.count(classList[0]))
# print(len(classList))
# print('===================')
if classList.count(classList[0]) == len(classList): #如果类别完全相同则停止继续划分
return classList[0]
# print(dataSet[0])
# print(len(labels))
# print('---------------')
if len(dataSet[0]) == 1 or len(labels) == 0: #遍历完所有特征时返回出现次数最多的类标签
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet) #选择最优特征
bestFeatLabel = labels[bestFeat] #最优特征的标签
featLabels.append(bestFeatLabel)
myTree = {bestFeatLabel:{}} #根据最优特征的标签生成树
del(labels[bestFeat]) #删除已经使用特征标签
featValues = [example[bestFeat] for example in dataSet] #得到训练集中所有最优特征的属性值
uniqueVals = set(featValues) #去掉重复的属性值
for value in uniqueVals: #遍历特征,创建决策树。
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels, featLabels)
return myTree
if __name__ == '__main__':
dataSet, labels = createDataSet()
featLabels = []
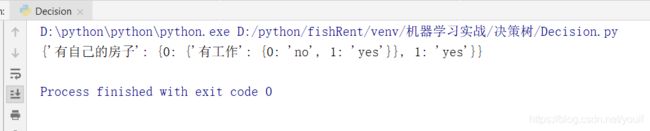
myTree = createTree(dataSet, labels, featLabels)
print(myTree)
6 C4.5:信息增益率
信息增益看似挺好用的,但是有没有什么问题呢?
ID3方法虽好,但是有一个问题就是,如果数据集包含ID这样的属性,构建出的决策树就会完全无效,因为ID的信息增益永远是最大的。
试想一下,你有15个样本,结果构建了一颗15叉树,这样确实模型结果是百分百正确,但是这样的树又有什么用呢? 如果来了一个ID为15的样本,根本没有办法进行预测。
于是ID3的发明人又提出了一种方法,就是C4.5,这个方法只是进行了小小改进,就解决了ID3的问题。不同于ID3采用信息增益进行划分,C4.5用的是信息增益率


7 CATR: Gini系数

CART分类树算法使用基尼系数来代替信息增益比,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益(比)是相反的。

8 过拟合与剪枝
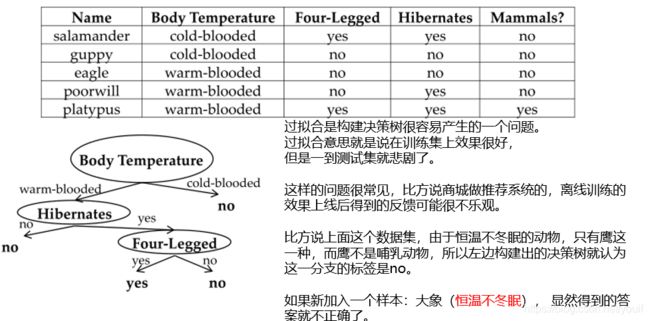
过拟合 Overfitting
一是增大训练集的规模,使得它能包含足够多的差异性。 但这样可能不太现实,因为我们实际使用的训练集一般都是很大的,但差异性是很多的,不可能包括进去,并且在有监督学习中我们要给每个训练样本贴标签,花费是比较大的。所以这不是一个好的解决方案。
二是剪枝,把复杂的树变得简单一些,这样就能避免一些极端情况,这是我们相对能容易点完成的解决方案。

不妨用左边的数据集验证一下剪枝的效果。
尽管训练集的错误率提高了,但剪枝后测试集的错误率减少了很多,所以剪枝后效果更好。
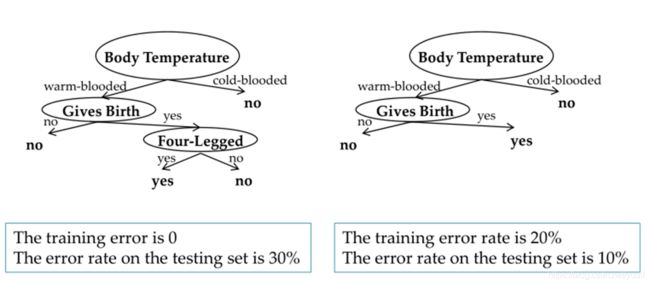
那么问题来了,说道剪枝,到底要怎么剪呢?
我们在使用决策树时,一般都是希望目标函数(也有说损失函数/误差函数/价值函数的)最小。
传统地有: e = 错误个数 / 总个数
但现在我们希望找到一种方法能够让目标函数在剪枝后有可能比剪枝前要小。
这是一个还在不断研究的课题,这里演示一种简单的方法,引入惩罚项α
剪枝方法: e = (错误个数 + α*叶子数)/ 总个数
9 决策树算法种类
(1)-ID3.
以信息增益作为树的分裂准则,该算法存在的不足:。
(a)- ID3没有考虑连续特征,比如长度,密度都是连续值,无法在ID3运用,如果- -定要运用ID3出来连续属性,那么要自己将连续特征离散化(办法非常多),
(b)-对于缺失值的情况没有做考虑
©-偏向于多值属性。例,如果存在唯–标识属性ID(每个样本的ID属性值都不相同),
则ID3会选择它作为优先分裂属性,这样虽然使得划分充分纯净,但这种划分对分类几乎亳无用处。
(2)-C4.5.
(a)以基于信息增益的增益率(gain ratio)作为树的分裂准则,解决了ID3的偏向于多值属性问题.
(b)内部自己考虑了连续属性离散化过程,所以克服了ID3的没有考虑连续特征问题。
©内部考虑了缺失值的自动处理策略。
(3)CART.
ID3和C4.5只能处理分类问题,而CART可以处理分类和回归问题,CART考虑问题非常全面,有较多优点,后期深入研究。
决策树基本的内容就是以上这些,但是这些仅仅是基础。决策树模型虽然简单,但是也是比较常用的,在各大竞赛以及一些顶尖会议的论文中不乏出现。像RF,GBDT( Gradient Boosting Decision Tree )这些更高级的方法大家不妨再作了解。
10 决策树鸢尾花实战
案例一
import pandas as pd
iris_data = pd.read_csv('iris.data')
iris_data.columns = ['sepal_length_cm', 'sepal_width_cm', 'petal_length_cm', 'petal_width_cm', 'class']
iris_data.head()
iris_data.describe()
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sb
sb.pairplot(iris_data.dropna(), hue='class') #去掉缺失值 不同特征之间类别分布图 hue使用指定变量为分类变量画图。参数类型:string (变量名)
from PIL import Image
img=Image.open('test.jpg')
plt.imshow(img)
plt.show()
img=Image.open('1.png') #山鸢尾花(Iris Setosa)
plt.imshow(img)
plt.show()
img=Image.open('2.png') #变色鸢尾花(Iris Versicolor)
plt.imshow(img)
plt.show()
img=Image.open('3.png') #维吉尼亚鸢尾花(Iris Virginica)
plt.imshow(img)
plt.show()
plt.figure(figsize=(10, 10)) #指定画图域
for column_index, column in enumerate(iris_data.columns):
if column == 'class':
continue
plt.subplot(2, 2, column_index + 1) #指定子图
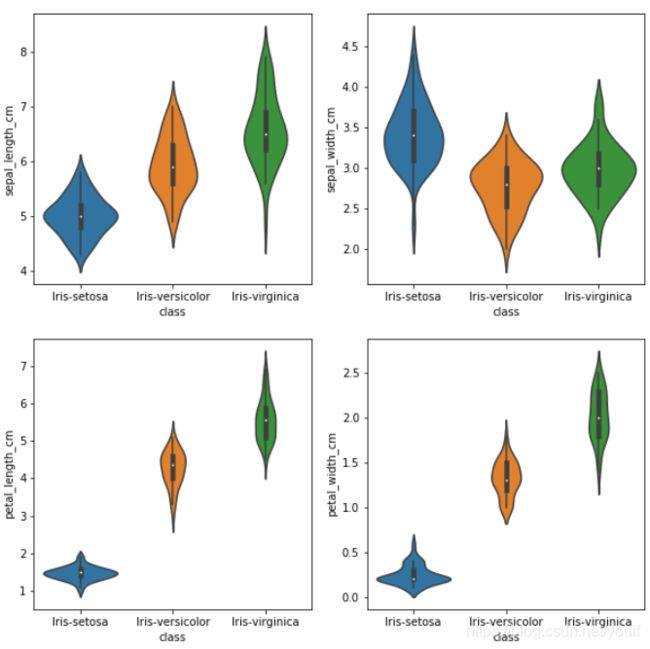
sb.violinplot(x='class', y=column, data=iris_data)#小提琴图 中间的黑色粗条表示四分位数范围,从其延伸的幼细黑线代表 95% 置信区间,
#而白点则为中位数。
from sklearn.model_selection import train_test_split
all_inputs = iris_data[['sepal_length_cm', 'sepal_width_cm',
'petal_length_cm', 'petal_width_cm']].values
all_classes = iris_data['class'].values
(training_inputs,
testing_inputs,
training_classes,
testing_classes) = train_test_split(all_inputs, all_classes, train_size=0.75, random_state=1)
from sklearn.tree import DecisionTreeClassifier
# 1.criterion gini or entropy
# 2.splitter best or random 前者是在所有特征中找最好的切分点 后者是在部分特征中(数据量大的时候)
# 3.max_features None(所有),log2,sqrt,N 特征小于50的时候一般使用所有的
# 4.max_depth 数据少或者特征少的时候可以不管这个值,如果模型样本量多,特征也多的情况下,可以尝试限制下
# 5.min_samples_split 如果某节点的样本数少于min_samples_split,则不会继续再尝试选择最优特征来进行划分
# 如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。
# 6.min_samples_leaf 这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被
# 剪枝,如果样本量不大,不需要管这个值,大些如10W可是尝试下5
# 7.min_weight_fraction_leaf 这个值限制了叶子节点所有样本权重和的最小值,如果小于这个值,则会和兄弟节点一起
# 被剪枝默认是0,就是不考虑权重问题。一般来说,如果我们有较多样本有缺失值,
# 或者分类树样本的分布类别偏差很大,就会引入样本权重,这时我们就要注意这个值了。
# 8.max_leaf_nodes 通过限制最大叶子节点数,可以防止过拟合,默认是"None”,即不限制最大的叶子节点数。
# 如果加了限制,算法会建立在最大叶子节点数内最优的决策树。
# 如果特征不多,可以不考虑这个值,但是如果特征分成多的话,可以加以限制
# 具体的值可以通过交叉验证得到。
# 9.class_weight 指定样本各类别的的权重,主要是为了防止训练集某些类别的样本过多
# 导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重
# 如果使用“balanced”,则算法会自己计算权重,样本量少的类别所对应的样本权重会高。
# 10.min_impurity_split 这个值限制了决策树的增长,如果某节点的不纯度
# (基尼系数,信息增益,均方差,绝对差)小于这个阈值
# 则该节点不再生成子节点。即为叶子节点 。
decision_tree_classifier = DecisionTreeClassifier()
# Train the classifier on the training set
decision_tree_classifier.fit(training_inputs, training_classes)
# Validate the classifier on the testing set using classification accuracy
decision_tree_classifier.score(testing_inputs, testing_classes)
![]()
案例二
决策树可视化环境搭建
scikit-learn中决策树的可视化一般需要安装graphviz。主要包括graphviz的安装和python的graphviz插件的安装。
第一步是安装graphviz。下载地址在:http://www.graphviz.org/。如果你是linux,可以用apt-get或者yum的方法安装。如果是windows,就在官网下载msi文件安装。无论是linux还是windows,装完后都要设置环境变量,将graphviz的bin目录加到PATH,比如我是windows,将C:/Program Files (x86)/Graphviz2.38/bin/加入了PATH
第二步是安装python插件graphviz: pip install graphviz
第三步是安装python插件pydotplus。这个没有什么好说的: pip install pydotplus
这样环境就搭好了,有时候python会很笨,仍然找不到graphviz,这时,可以在代码里面加入这一行:
os.environ[“PATH”] += os.pathsep + ‘C:/Program Files (x86)/Graphviz2.38/bin/’
注意后面的路径是你自己的graphviz的bin目录。
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn import tree
iris = load_iris()
iris_data = iris['data']
iris_data
iris_target = iris['target']
iris_target
clf = tree.DecisionTreeClassifier()
clf = clf.fit(iris.data, iris.target)
with open("iris.dot", 'w') as f: #现在可以将模型存入dot文件iris.dot。
f = tree.export_graphviz(clf, out_file=f)
from IPython.display import Image
import pydotplus
import os
os.environ["PATH"] += os.pathsep + 'D:/python/graphvizview/bin'
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=iris.feature_names,
class_names=iris.target_names,
filled=True, rounded=True,
special_characters=True) #兼容性字符
graph = pydotplus.graph_from_dot_data(dot_data)
Image(graph.create_png()) #比较推荐的做法,因为这样可以直接把图产生在ipython的notebook。
dot_data = tree.export_graphviz(clf, out_file=None)
graph = pydotplus.graph_from_dot_data(dot_data)
graph.write_pdf("iris.pdf") #用pydotplus生成iris.pdf。
案例三
这里给一个限制决策树层数为4的DecisionTreeClassifier例子。
from itertools import product
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
# 仍然使用自带的iris数据
iris = datasets.load_iris()
X = iris.data[:, [0, 2]]
y = iris.target
# 训练模型,限制树的最大深度4
clf = DecisionTreeClassifier(max_depth=4,criterion="entropy")
#拟合模型
clf.fit(X, y)
# 画图
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
np.arange(y_min, y_max, 0.1))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.4) #画等高线
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.8)
plt.show()
from IPython.display import Image
from sklearn import tree
import pydotplus
import os
os.environ["PATH"] += os.pathsep + 'D:/python/graphvizview/bin'
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=["sepal length","sepal width"],
class_names=iris.target_names,
filled=True, rounded=True, #树节点为圆角矩形 #由颜色标识不纯度
special_characters=True) #兼容性字符
graph = pydotplus.graph_from_dot_data(dot_data)
Image(graph.create_png())
个人微信公众号,专注于学习资源、笔记分享,欢迎关注。我们一起成长,一起学习。一直纯真着,善良着,温情地热爱生活。
![]()
If you’re brave enough to say Goodbye, life will reward you with a new Hello.
只要你勇敢地说出再见,生活一定会赐予你一个新的开始。
数据链接:https://pan.baidu.com/s/1CvCKqaDb0g3MKzLaaoexQg
提取码:3s4t
XiangLin
2020年3月5日于重庆城口
好好学习,天天向上,终有所获