(原创)呜呜祖啦滤波器FPGA实现
摘要:研究一种采用FPGA实现128阶FIR音频滤波器,在满足滤波要求的情况下,所耗资源最少;讨论窗函数的选择、滤波器的结构、系数的量化问题;重点在于如何去实现和如何去仿真验证,而不仅仅是理论讨论,涉及到MATLAB与Modelsim联合仿真验证。
1、引言
2010南非世界杯,球迷们的豪华盛宴,但遗憾的是南非球迷们在现场吹起了呜呜祖啦,这种声音不仅很刺耳,还覆盖掉了足球场上的一切声音,使得在呜呜祖啦滤波器FPGA实现.doc司迅速的推出了一款呜呜祖啦滤波器,但为什么转播的时候没有采用这款滤波器先滤除呜呜祖啦声音后再传送到电视机呢?一个很重要的原因是,这款滤波器是纯软件制作,速度无法达到直播所需的高速,而基于硬件实现的FPGA方案却能很好的满足这一要求,所以研究这种方案很既有吸引力。
2、MATLAB计算出滤波器系数
本设计采用的是有限脉冲响应滤波器(FIR),汉宁窗,高通,具体设计如下:
 代码
代码
wp
=
0.17
*
pi; ws
=
0.12
*
pi;
%
输入设计指标
deltaw
=
wp
-
ws;
%
计算过渡带的宽度
N0
=
ceil(
6.2
*
pi
/
deltaw);
%
按汉宁窗窗计算滤波器长度N0
N
=
N0
+
mod(N0
+
1
,
2
)
%
为实现FIR类型I偶对称滤波器,应确保N为奇数
windows
=
(hanning(N))
'
; % 使用汉宁窗,并将列向量变为行向量
wc
=
(ws
+
wp)
/
2
;
%
截止频率取通阻带频率的平均值
hd
=
ideal_lp(pi,N)
-
ideal_lp(wc,N);
%
建立理想高通滤波器
b
=
hd.
*
windows;
%
求FIR系统函数系数
[db,mag,pha,grd,w]
=
freqz_m(b,
1
);
%
求解频率特性
n
=
0
:N
-
1
; dw
=
2
*
pi
/
1000
;
%
dw为频率分辨率,将0—2π 分成为1000份
Rp
=-
(min(db(wp
/
dw
+
1
:
501
)))
%
检验通带波动
As
=-
round(max(db(
1
:ws
/
dw
+
1
)))
%
检验最小阻带衰减
滤波器参数初步设定了之后,导入音频数据,实现滤波,进行快速傅里叶变换,观察滤波前与滤波后的频谱,试听滤波前与滤波后的音频,反复调整参数,直到达到所需效果,但有一点必须要考虑,那就是抽头系数N越大,滤波效果越好,但所耗资源越多。折合这两个因数,综合考虑,本设计决定采用125点对称抽头系数,125点既可以达到很好的效果,又可以不必消耗过多的资源,具体设计如下:
 代码
代码
[y,fs,bits]
=
wavread(
'
D:\2014.wav
'
);
%
读入音频文件
Y
=
filter(b,
1
,y);
%
实现数字滤波
t
=
(
0
:length(y)
-
1
)
/
fs;
%
计算数据时刻
subplot(
3
,
2
,
1
);plot(t,y);
%
绘制原波形图
title(
'
原信号波形图
'
);
%
加标题
subplot(
3
,
2
,
2
);plot(t,Y);
%
绘制滤波后波形图
title(
'
滤波后波形图
'
);
%
加标题
xf
=
fft(y);
%
作傅里叶变换求原频谱
yf
=
fft(Y);
%
作傅里叶变换求滤波后频谱
fm
=
3000
*
length(xf)
/
fs;
%
确定绘频谱图的上限频率
f
=
(
0
:fm)
*
fs
/
length(xf);
%
确定绘频谱图的频率刻度
subplot(
3
,
2
,
3
);plot(f,abs(xf(
1
:length(f))));
%
绘制原波形频谱图
title(
'
原信号频谱图
'
);
%
加标题
subplot(
3
,
2
,
4
);plot(f,abs(yf(
1
:length(f))));
%
绘制滤波后频谱图
title(
'
滤波后信号频谱图
'
);
%
加标题
subplot(
3
,
2
,
5
),plot(w
/
pi,db);
axis([
0
,
1
,
-
100
,
10
]);
title(
'
幅度频率响应
'
);
%
加标题
set
(gca,
'
XTickMode
'
,
'
manual
'
,
'
XTick
'
,...
[
0
,ws
/
pi,wp
/
pi,
1
]);
set
(gca,
'
YTickMode
'
,
'
manual
'
,
'
YTick
'
,...
[
-
100
,
-
20
,
-
3
,
0
]);grid
sound(Y,fs,bits);
%
播放音频
sound(y,fs,bits);
wavwrite(Y,fs,bits,
'
D:\4014.wav
'
);
%
读出音频
以上的两段程序可以综合一起,做成一个high_pass_hanning.m文件。运行该程序可以得到125个具有对称性的抽头系数。(系数都是归一化了的,如-1.0023e-007、0.8550)以下是上面调用到的一个小函数:
function hd
=
ideal_lp(wc,N)
tao
=
(N
-
1
)
/
2
;
n
=
[
0
:(N
-
1
)];
m
=
n
-
tao
+
eps;
hd
=
sin(wc
*
m).
/
(pi
*
m);
end
3、MATLAB对系数进行处理
FPGA无法对小数直接进行运算,故需对系数进行处理,转换为FPGA
能直接进行运算的正整数,负数用其补码表示,具体设计如下:
q
=
quantizer([
24
23
]);
%
23代表截取小数点后面的位数,24代表转换之后的位数
b0
=
num2hex(q,b);
%
有符号小数形式,转换为正整数形式,最高位为符号位
经这么一转换后,抽头系数就变成了正整数的形式了,以十六进制表示,位数为24位,最高位为符号位。(MATLAB的一些函数的用法,可以在命令窗口直接输入help+命令,如help num2hex,即可了解该函数的使用,MATLAB很人性化吧!)
4、Verilog HDL 实现24*8的乘法器
上面提到FPGA无法对小数直接进行运算,故转换成了正整数形式,但是我
们在进行运算的时候,时刻要警惕,我们进行运算的是小数,而不是整数,(它们的不同点就是:整数在高位可以补0,而小数则是在低位可以补0,如整数
 代码
代码
module
signed_mult24_8 (
mul_a,
mul_b,
mul_out,
clk,
rst_n
);
parameter
MUL_WIDTH_a
=
24
;
parameter
MUL_WIDTH_b
=
8
;
parameter
MUL_RESULT
=
31
;
input
[MUL_WIDTH_a
-
1
:
0
] mul_a;
input
[MUL_WIDTH_b
-
1
:
0
] mul_b;
input
clk;
input
rst_n;
output
[MUL_RESULT
-
1
:
0
] mul_out;
reg
[MUL_RESULT
-
1
:
0
] mul_out;
reg
[MUL_RESULT
-
1
:
0
] mul_out_reg;
reg
msb;
reg
msb_reg_0;
reg
msb_reg_1;
reg
msb_reg_2;
reg
[MUL_WIDTH_a
-
1
:
0
] mul_a_reg;
reg
[MUL_WIDTH_b
-
1
:
0
] mul_b_reg;
reg
[MUL_RESULT
-
2
:
0
] stored0;
reg
[MUL_RESULT
-
2
:
0
] stored1;
reg
[MUL_RESULT
-
2
:
0
] stored2;
reg
[MUL_RESULT
-
2
:
0
] stored3;
reg
[MUL_RESULT
-
2
:
0
] stored4;
reg
[MUL_RESULT
-
2
:
0
] stored5;
reg
[MUL_RESULT
-
2
:
0
] stored6;
reg
[MUL_RESULT
-
2
:
0
] add0_0;
reg
[MUL_RESULT
-
2
:
0
] add0_1;
reg
[MUL_RESULT
-
2
:
0
] add0_2;
reg
[MUL_RESULT
-
2
:
0
] add0_3;
reg
[MUL_RESULT
-
2
:
0
] add1_0;
reg
[MUL_RESULT
-
2
:
0
] add1_1;
reg
[MUL_RESULT
-
2
:
0
] add2_0;
always
@ (
posedge
clk
or
negedge
rst_n )
begin
if
(
!
rst_n )
begin
mul_a_reg
<=
24
'
b0;
mul_b_reg
<=
8
'
b0;
stored0
<=
30
'
b0;
stored1
<=
30
'
b0;
stored2
<=
30
'
b0;
stored3
<=
30
'
b0;
stored4
<=
30
'
b0;
stored5
<=
30
'
b0;
stored6
<=
30
'
b0;
add0_0
<=
30
'
b0;
add0_1
<=
30
'
b0;
add0_2
<=
30
'
b0;
add0_3
<=
30
'
b0;
add1_0
<=
30
'
b0;
add1_1
<=
30
'
b0;
add2_0
<=
30
'
b0;
msb
<=
1
'
b0;
msb_reg_0
<=
1
'
b0;
msb_reg_1
<=
1
'
b0;
msb_reg_2
<=
1
'
b0;
mul_out_reg
<=
31
'
b0;
mul_out
<=
31
'
b0;
end
else
begin
mul_a_reg
<=
(mul_a[
23
]
==
0
)
?
mul_a : {mul_a[
23
],
~
mul_a[
22
:
0
]
+
1
'
b1};
mul_b_reg
<=
(mul_b[
7
]
==
0
)
?
mul_b : {mul_b[
7
],
~
mul_b[
6
:
0
]
+
1
'
b1};
msb_reg_0
<=
mul_a_reg[
23
]
^
mul_b_reg[
7
];
msb_reg_1
<=
msb_reg_0;
msb_reg_2
<=
msb_reg_1;
msb
<=
msb_reg_2;
stored0
<=
mul_b_reg[
0
]
?
{
7
'
b0,mul_a_reg[22:0]} : 30
'
b0;
stored1
<=
mul_b_reg[
1
]
?
{
6
'
b0,mul_a_reg[22:0],1
'
b0} :
30
'
b0;
stored2
<=
mul_b_reg[
2
]
?
{
5
'
b0,mul_a_reg[22:0],2
'
b0} :
30
'
b0;
stored3
<=
mul_b_reg[
3
]
?
{
4
'
b0,mul_a_reg[22:0],3
'
b0} :
30
'
b0;
stored4
<=
mul_b_reg[
4
]
?
{
3
'
b0,mul_a_reg[22:0],4
'
b0} :
30
'
b0;
stored5
<=
mul_b_reg[
5
]
?
{
2
'
b0,mul_a_reg[22:0],5
'
b0} :
30
'
b0;
stored6
<=
mul_b_reg[
6
]
?
{
1
'
b0,mul_a_reg[22:0],6
'
b0} :
30
'
b0;
add0_0
<=
stored0
+
stored1;
add0_1
<=
stored2
+
stored3;
add0_2
<=
stored4
+
stored5;
add0_3
<=
stored6;
add1_0
<=
add0_0
+
add0_1;
add1_1
<=
add0_2
+
add0_3;
add2_0
<=
add1_0
+
add1_1;
mul_out_reg
<=
(add2_0
==
0
)
?
31
'
b0 : {msb,add2_0[29:0]};
mul_out
<=
(mul_out_reg
==
0
)
?
31
'
b0 : (mul_out_reg[30]==0)? mul_out_reg :
{mul_out_reg[
30
],
~
mul_out_reg[
29
:
0
]
+
1
'
b1};
end
end
endmodule
这里面有几个地方需要注意:1、每个二叉树后面需要使用一个流水寄存器,以至达到每个时钟周期完成一次运算。2、对于负数需把其补码还原为原码再进行运算,若运算结果为负数,需转换为补码再输出。3、对于输入的两个数,当一个为0,一个为负数时,需要特别处理,否则结果输出为-1,明显的出错了。4、符号位与数据位需要时钟同步,不然也会出错,因为符号位运算所需时钟周期较少,而数据运算所需周期较多。
5、采用改进的串行结构进行滤波器设计
串行结构所耗资源最少,只需一个乘法器和一些加法器,而速度很慢,据抽头系数个数而定;并行结构所耗资源最多,据抽头系数个数而定,但速度最快,一个时钟周期即可完成一次滤波;分布式结构,耗资源不是很多,而速度也不是很快,基于串行和并行之间,据输入数据的位数来决定。(以上说法不一定正确,但对于大多数情况都是这样的)本设计采用的是改进的串行结构(先加后乘),N=125,系数具有对称性,故只需63个时钟周期,即可完成一次滤波,耗资源很少,只需一个乘法器和62个加法器。本设计是针对音频信号进行滤波,音频信号频率很低,所以即使完成一次滤波需要63个时钟周期,但也能很好的满足要求,且能有效的减少所耗资源,具体设计如下:
 代码
代码
module
ser_fir (clk,rst_n,fir_in,fir_out );
parameter
FIR_TAP
=
125
;
parameter
FIR_TAPHALF
=
63
;
parameter
IDATA_WIDTH
=
8
;
//
parameter PDATA_WIDTH = 9;
parameter
COEFF_WIDTH
=
24
;
parameter
OUT_WIDTH
=
31
;
input
clk;
input
rst_n;
input
[IDATA_WIDTH
-
1
:
0
] fir_in;
output
[OUT_WIDTH
-
1
:
0
] fir_out;
reg
[OUT_WIDTH
-
1
:
0
] fir_out;
reg
[IDATA_WIDTH
-
1
:
0
] fir_in_reg;
reg
[IDATA_WIDTH
-
1
:
0
] shift_buf[FIR_TAP
-
1
:
0
];
reg
[IDATA_WIDTH
-
1
:
0
] add[FIR_TAPHALF
-
1
:
0
];
reg
[COEFF_WIDTH
-
1
:
0
] cof[FIR_TAPHALF
-
1
:
0
];
reg
[COEFF_WIDTH
-
1
:
0
] cof_reg_maca;
reg
[IDATA_WIDTH
-
1
:
0
] add_reg_macb;
wire
[IDATA_WIDTH
+
COEFF_WIDTH
-
2
:
0
] result;
reg
[OUT_WIDTH:
0
] sum;
reg
[
5
:
0
] count;
integer
i,j,k0,k1;
always
@ (
posedge
clk
or
negedge
rst_n )
begin
if
(
!
rst_n )
begin
cof[
0
]
=
24
'
hffffff;
cof[
1
]
=
24
'
hffffcd;
cof[
2
]
=
24
'
hffff36;
cof[
3
]
=
24
'
hfffe46;
cof[
4
]
=
24
'
hfffd54;
cof[
5
]
=
24
'
hfffcfe;
cof[
6
]
=
24
'
hfffdee;
cof[
7
]
=
24
'
h000095;
cof[
8
]
=
24
'
h0004de;
cof[
9
]
=
24
'
h000a03;
cof[
10
]
=
24
'
h000e99;
cof[
11
]
=
24
'
h0010cf;
cof[
12
]
=
24
'
h000ef6;
cof[
13
]
=
24
'
h000810;
cof[
14
]
=
24
'
hfffc5d;
cof[
15
]
=
24
'
hffed9d;
cof[
16
]
=
24
'
hffdefc;
cof[
17
]
=
24
'
hffd47f;
cof[
18
]
=
24
'
hffd220;
cof[
19
]
=
24
'
hffdaa9;
cof[
20
]
=
24
'
hffeead;
cof[
21
]
=
24
'
h000be4;
cof[
22
]
=
24
'
h002d1d;
cof[
23
]
=
24
'
h004b00;
cof[
24
]
=
24
'
h005d7c;
cof[
25
]
=
24
'
h005dab;
cof[
26
]
=
24
'
h0047cb;
cof[
27
]
=
24
'
h001cbe;
cof[
28
]
=
24
'
hffe2b3;
cof[
29
]
=
24
'
hffa492;
cof[
30
]
=
24
'
hff7036;
cof[
31
]
=
24
'
hff5398;
cof[
32
]
=
24
'
hff5988;
cof[
33
]
=
24
'
hff8699;
cof[
34
]
=
24
'
hffd709;
cof[
35
]
=
24
'
h003e4f;
cof[
36
]
=
24
'
h00a893;
cof[
37
]
=
24
'
h00fe1c;
cof[
38
]
=
24
'
h01281a;
cof[
39
]
=
24
'
h0115f7;
cof[
40
]
=
24
'
h00c208;
cof[
41
]
=
24
'
h00347c;
cof[
42
]
=
24
'
hff83b3;
cof[
43
]
=
24
'
hfed17a;
cof[
44
]
=
24
'
hfe456e;
cof[
45
]
=
24
'
hfe0550;
cof[
46
]
=
24
'
hfe2ca1;
cof[
47
]
=
24
'
hfec52b;
cof[
48
]
=
24
'
hffc216;
cof[
49
]
=
24
'
h00fed6;
cof[
50
]
=
24
'
h024291;
cof[
51
]
=
24
'
h0347d1;
cof[
52
]
=
24
'
h03c777;
cof[
53
]
=
24
'
h03853a;
cof[
54
]
=
24
'
h025b72;
cof[
55
]
=
24
'
h004413;
cof[
56
]
=
24
'
hfd5cef;
cof[
57
]
=
24
'
hf9e642;
cof[
58
]
=
24
'
hf63b5d;
cof[
59
]
=
24
'
hf2c675;
cof[
60
]
=
24
'
heff16e;
cof[
61
]
=
24
'
hee161e;
cof[
62
]
=
24
'
h6d70a3;
end
end
always
@ (
posedge
clk
or
negedge
rst_n )
begin
if
(
!
rst_n )
fir_in_reg
<=
8
'
b0;
else
if
( count
==
6
'
d63 )
fir_in_reg
<=
fir_in;
end
always
@ (
posedge
clk
or
negedge
rst_n )
begin
if
(
!
rst_n )
for
( i
=
0
;i
<=
FIR_TAP
-
1
;i
=
i
+
1
)
shift_buf[i]
<=
8
'
b0;
else
if
( count
==
6
'
d63 )
begin
for
( j
=
0
;j
<
FIR_TAP
-
1
;j
=
j
+
1
)
shift_buf[j
+
1
]
<=
shift_buf[j];
shift_buf[
0
]
<=
fir_in_reg;
end
end
always
@ (
posedge
clk
or
negedge
rst_n )
begin
if
(
!
rst_n )
for
( k0
=
0
;k0
<=
FIR_TAPHALF
-
1
;k0
=
k0
+
1
)
add[k0]
<=
8
'
b0;
else
if
( count
==
6
'
d63 )
begin
for
( k1
=
0
;k1
<=
FIR_TAPHALF
-
2
;k1
=
k1
+
1
)
add[k1]
<=
shift_buf[k1]
+
shift_buf[
124
-
k1];
add[
62
]
<=
shift_buf[
62
];
end
end
always
@ (
posedge
clk
or
negedge
rst_n )
begin
if
(
!
rst_n )
count
<=
6
'
b0;
else
if
( count
==
6
'
d63 )
count
<=
6
'
b0;
else
count
<=
count
+
1
'
b1;
end
always
@ (
posedge
clk
or
negedge
rst_n )
begin
if
(
!
rst_n )
begin
cof_reg_maca
<=
24
'
b0;
add_reg_macb
<=
8
'
b0;
end
else
if
( count
<=
6
'
d62 )
begin
cof_reg_maca
<=
cof[count];
add_reg_macb
<=
add[count];
end
else
if
( count
==
6
'
d63 )
begin
cof_reg_maca
<=
24
'
b0;
add_reg_macb
<=
8
'
b0;
end
end
signed_mult24_8 mul_0 (
.mul_a(cof_reg_maca),
.mul_b(add_reg_macb),
.mul_out(result),
.clk(clk),
.rst_n(rst_n)
);
wire
[OUT_WIDTH:
0
] result_out
=
{result[
30
],result[
30
:
0
]};
always
@ (
posedge
clk
or
negedge
rst_n )
begin
if
(
!
rst_n )
sum
<=
32
'
b0;
else
if
( count
==
6
'
b0)
sum
<=
32
'
b0;
else
sum
<=
sum
+
result_out;
end
always
@ (
posedge
clk
or
negedge
rst_n )
begin
if
(
!
rst_n )
fir_out
<=
31
'
b0;
else
if
( count
==
6
'
b0 )
fir_out
<=
sum[
30
:
0
];
end
endmodule
6、Modelsim对设计好的滤波器进行仿真验证
这里需要用Modelsim 进行仿真验证,而不用FPGA厂商提供的集成软件,Modelsim有很多优点,特别对于数字信号处理方面的仿真,我们可以通过写Testbench进行仿真。通过Testbench对记事本文件数据读入,处理后再读出到记事本文件。这样做的好处是,我们可以结合MATLAB一起进行仿真验证,首先是从MATLAB把未经滤波的音频数据读出到记事本文件,然后送给Modelsim作为数据输入源,经设计好了的滤波器滤波处理之后,把数据输出到另一个记事本文件,最后MATLAB把刚才处理过了的音频数据文件读出数据,进行快速傅里叶变换,观察其频谱,试听其音频,跟直接在MATLAB进行滤波处理的音频比较,这样便可以很清楚的看到自己设计的滤波器滤波效果与直接MATLAB滤波的效果的对比了,这时即可验证FPGA设计的正确性了,这种验证方法,对于数字信号处理非常的有效,所以极力推荐,具体设计如下:
 代码
代码
`define auto_init
`timescale 1ns
/
1ns
`define INPUT_FILE
"
fir_in8.txt
"
`define OUTPUT_FILE
"
fir_out31.txt
"
module
test_ser_fir ();
parameter
NOOFDATA
=
40000
;
parameter
FIR_TAP
=
125
;
parameter
FIR_TAPHALF
=
63
;
parameter
IDATA_WIDTH
=
8
;
//
parameter PDATA_WIDTH = 9;
parameter
COEFF_WIDTH
=
24
;
parameter
OUT_WIDTH
=
31
;
parameter
CLK_CYCLE
=
20
;
parameter
CLK_HCYCLE
=
10
;
reg
clk;
reg
rst_n;
reg
[IDATA_WIDTH
-
1
:
0
] fir_in;
wire
[OUT_WIDTH
-
1
:
0
] fir_out;
reg
[IDATA_WIDTH
-
1
:
0
] memb [
1
:NOOFDATA];
reg
[OUT_WIDTH
-
1
:
0
] membyte [
0
:NOOFDATA
-
1
];
reg
write;
integer
handle;
reg
[
18
:
0
] count_w;
reg
[
5
:
0
] regcount;
reg
[
18
:
0
] k;
reg
[
18
:
0
] k0;
ser_fir dut ( clk,rst_n,fir_in,fir_out );
`ifdef auto_init
initial
begin
$readmemb(`INPUT_FILE,memb);
regcount
=
0
;
count_w
=
0
;
handle
=
0
;
clk
=
0
;
k
=
0
;
k0
=
0
;
rst_n
=
1
'
b0;
#(
10
*
CLK_CYCLE
+
CLK_HCYCLE) rst_n
=
1
'
b1;
end
`endif
always
#CLK_HCYCLE clk
=
~
clk;
always
@ (
posedge
clk
or
negedge
rst_n )
begin
if
(
!
rst_n )
regcount
<=
6
'
b0;
else
if
( regcount
==
6
'
d63 )
regcount
<=
6
'
b0;
else
regcount
<=
regcount
+
1
'
b1;
end
always
@ (
posedge
clk
or
negedge
rst_n )
begin
if
(
!
rst_n )
begin
fir_in
<=
10
'
b0;
k
<=
19
'
d1;
end
else
if
( regcount
==
6
'
d63 )
begin
k
<=
k
+
1
'
b1;
fir_in
<=
memb[k];
end
end
always
@ (
posedge
clk
or
negedge
rst_n )
begin
if
(
!
rst_n )
k0
<=
19
'
b0;
else
if
( regcount
==
6
'
b0 )
begin
k0
<=
k0
+
1
'
b1;
membyte[k0]
<=
fir_out;
end
end
always
@ (
posedge
clk
or
negedge
rst_n )
begin
if
(
!
rst_n )
write
<=
1
'
b0;
else
begin
if
( k
==
NOOFDATA )
write
<=
1
'
b1;
end
end
always
@ (
posedge
write )
begin
handle
=
$fopen(`OUTPUT_FILE);
$display(
"
writing results to file...
"
);
for
( count_w
=
0
;count_w
<
NOOFDATA;count_w
=
count_w
+
1
)
begin
$fdisplay(handle,
"
%d
"
,membyte[count_w]);
$display(
"
%d
"
,membyte[count_w]);
end
$fclose(handle);
end
endmodule
测试程序也很简单吧!非常短!但这里有几个需要注意的地方:1、记事本文件的地址是从1开始的,所以赋初值为1,而不是0;2、Testbench对记事本文件数据读取时,只能识别二进制数据,而写入记事本文件时则可写成十六进制、十进制、二进制等。MATLAB对记事本文件的操作,具体设计如下:
 代码
代码
function var
=
txtfile_rt(filename,width,depth)
%
filename中的数是10进制的数,负数以补码形式表示, var为定点数
%
Created by maqingbiao
%
[email protected]
%
filename
--
the name of the file to be created,eg,
"
a.txt
"
,
string
;
%
var
----
the data to be writed to the file;
%
width
--
the word size of the data,width
>=
1
,
int
;
%
depth
--
the number of the data to be writed,
int
;
fid
=
fopen(filename,
'
rt
'
);
for
i
=
1
:depth
var_d(i)
=
fscanf(fid,
'
%d
'
,
1
);
end
fclose(fid);
q
=
quantizer([(width
+
1
) width]);
var_h
=
dec2hex(var_d);
var
=
hex2num(q,var_h);
end
我发现在MATLAB把数据写入记事本的时候,不能识别二进制,所以就不能使用直接写入数据的方法,而是手工拷贝的,我要拷贝的是30秒钟的音频数据,数据总量有32万个之多,由于MATLAB显示的原因,一次不能显示完32万个,所以我分8次拷贝,具体设计如下:
 代码
代码
q
=
quantizer([
8
7
]);
%
7代表截取小数点后面的位数,8代表转换之后的位数
y
=
y(:,
1
);
%
y为音频数据,为二维的,左右声道,只需取其中一维处理即可
yy
=
num2hex(q,y);
%
小数转十六进制
yyy
=
hex2dec(yy);
%
十六进制转十进制
y
=
yyy;
y1
=
y(
1
:
40000
);
%
取y的前4万个数据
y2
=
y(
40001
:
80000
);
y3
=
y(
80001
:
120000
);
y4
=
y(
120001
:
160000
);
y5
=
y(
160001
:
200000
);
y6
=
y(
200001
:
240000
);
y7
=
y(
240001
:
280000
);
y8
=
y(
280001
:
320000
);
y11
=
dec2bin(y1);
%
十进制转二进制
y12
=
dec2bin(y2);
y13
=
dec2bin(y3);
y14
=
dec2bin(y4);
y15
=
dec2bin(y5);
y16
=
dec2bin(y6);
y17
=
dec2bin(y7);
y18
=
dec2bin(y8);
MATLAB滤波与FPGA滤波效果对比,wuwuzula.m文件,具体设计如下:
运行该程序,得到结果如下,本设计滤波效果还可以吧!哈哈!
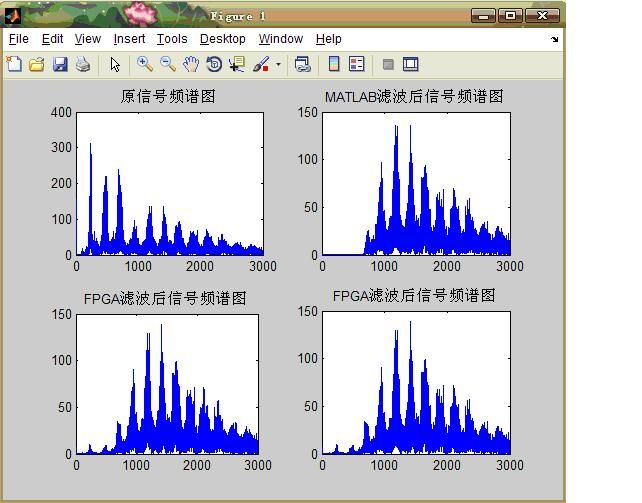
以上的音频文件,是从互联网上下载一段2010世界杯视频下来,然后经音频提取软件,把这段视频中的音频提取下来,再经截断后得到的一小段含有呜呜祖啦声音的音频文件,需要注意的是音频文件需要转成.WAV格式,因为MATLAB只能识别这种格式的文件。
(设计到此结束)
参考文献:《基于Verilog HDL的数字系统应用设计》王钿、卓兴旺编著。
《数字信号处理的FPGA实现》第二版刘凌 译。
《数字信号处理实验》MATLAB版,刘舒帆、费诺、陆辉编著
 代码
代码
wp
=
0.17
*
pi; ws
=
0.12
*
pi;
%
输入设计指标
deltaw
=
wp
-
ws;
%
计算过渡带的宽度
N0
=
ceil(
6.2
*
pi
/
deltaw);
%
按汉宁窗窗计算滤波器长度N0
N
=
N0
+
mod(N0
+
1
,
2
)
%
为实现FIR类型I偶对称滤波器,应确保N为奇数
windows
=
(hanning(N))
'
; % 使用汉宁窗,并将列向量变为行向量
wc
=
(ws
+
wp)
/
2
;
%
截止频率取通阻带频率的平均值
hd
=
ideal_lp(pi,N)
-
ideal_lp(wc,N);
%
建立理想高通滤波器
b
=
hd.
*
windows;
%
求FIR系统函数系数
[db,mag,pha,grd,w]
=
freqz_m(b,
1
);
%
求解频率特性
n
=
0
:N
-
1
; dw
=
2
*
pi
/
1000
;
%
dw为频率分辨率,将0—2π 分成为1000份
Rp
=-
(min(db(wp
/
dw
+
1
:
501
)))
%
检验通带波动
As
=-
round(max(db(
1
:ws
/
dw
+
1
)))
%
检验最小阻带衰减
[y,fs,bits]
=
wavread(
'
D:\2014.wav
'
);
%
读入音频文件
Y
=
filter(b,
1
,y);
%
实现数字滤波
y11
=
y(:,
1
);
y11
=
y(
1
:
40000
);
y
=
y11;
y22
=
Y(:,
1
);
y22
=
y22(
1
:
40000
);
Y
=
y22;
YY
=
txtfile_rt(
'
fir_out31.txt
'
,
30
,
40000
);
t
=
(
0
:length(y)
-
1
)
/
fs;
%
计算数据时刻
xf
=
fft(y);
%
作傅里叶变换求原频谱
yf
=
fft(Y);
%
作傅里叶变换求MATLAB滤波后频谱
yyf
=
fft(YY);
%
作傅里叶变换求FPGA滤波后频谱
fm
=
3000
*
length(xf)
/
fs;
%
确定绘频谱图的上限频率
f
=
(
0
:fm)
*
fs
/
length(xf);
%
确定绘频谱图的频率刻度
subplot(
2
,
2
,
1
);plot(f,abs(xf(
1
:length(f))));
%
绘制原波形频谱图
title(
'
原信号频谱图
'
);
%
加标题
subplot(
2
,
2
,
2
);plot(f,abs(yf(
1
:length(f))));
%
绘制MATLAB滤波后频谱图
title(
'
MATLAB滤波后信号频谱图
'
);
%
加标题
subplot(
2
,
2
,
3
);plot(f,abs(yyf(
1
:length(f))));
%
绘制FPGA滤波后频谱图
title(
'
FPGA滤波后信号频谱图
'
);
%
加标题
subplot(
2
,
2
,
4
);plot(f,abs(yyf(
1
:length(f))));
%
绘制FPGA滤波后频谱图
title(
'
FPGA滤波后信号频谱图
'
);
%
加标题
