机器学习——逻辑回归（梯度下降法、牛顿法）
机器学习——逻辑回归
- 一、实验题目
- 二、实验目的
- 三、实验平台
- 四、基本原理
-
- 1. 逻辑回归
- 2. 损失函数
- 五、实验步骤
-
- 1. 数据可视化
- 2. 将线性回归参数初始化为0，计算代价函数(cost function)的初始值
- 3. 选择一种优化方法求解逻辑回归参数
-
- 3.1. 梯度下降法
- 3.2. 牛顿迭代法
- 4. 某学生两次考试成绩分别为 42、85，预测其被录取的概率
- 5. 画出分类边界
- 六、程序清单
代码见https://pan.baidu.com/s/17OD94C71-J1u_lY3zN8lUQ （提取码：vp13），仅供参考
一、实验题目
- 主题：逻辑回归
- 描述：假设你是某大学招生主管，你想根据两次考试的结果决定每个申请者的录取
机会。现有以往申请者的历史数据，可以此作为训练集建立逻辑回归模型，并用
其预测某学生能否被大学录取。 - 数据集：文件 ex2data1.txt ，第一列、第二列分别表示申请者两次
考试的成绩，第三列表示录取结果（1 表示录取，0 表示不录取）。
二、实验目的
- 理解逻辑回归模型
- 掌握逻辑回归模型的参数估计算法
三、实验平台
- 硬件：计算机
- 操作系统：WINDOWS
- 编程软件：Pycharm
- 开发语言：python
四、基本原理
注：基本原理是我们在学习逻辑回归过程中的一些总结，包括为什么要选择对数损失函数等，可跳过。
1. 逻辑回归
逻辑回归就是将样本的特征可样本发生的概率联合起来，概率就是一个数，所以就是解决分类问题，一般解决二分类问题。
对于线性回归中，f ( x ) = w T x + b ，这里 f ( x ) 的范围为[ − ∞ , + ∞ ]，说明通过线性回归中我们可以求得任意的一个值。对于逻辑回归来说就是概率，这个概率取值需要在区间[0,1]内，通常我们使用Sigmoid函数表示。
Sigmoid函数其表达式为（2）
最终我们可以通过Sigmoid函数求出对于每组自变量使得因变量预测为1的概率P；
即：
（当P>0.5时预测为1，小于0.5为0）
在分类情况下，经过学习后的LR分类器其实就是一组权值 ，当有测试样本输入时，这组权值与测试数据按照加权得到 
之后按照Sigmoid函数的形式求出
，从而去判断每个测试样本所属的类别。
2. 损失函数
实验一我们做线性回归模型时，给出了线性回归的代价函数的形式（误差平方和函数），具体形式如： 
但是并不能应用到逻辑回归中，这是因为LR的假设函数的外层函数是Sigmoid函数，Sigmoid函数是一个复杂的非线性函数，这就使得我们将逻辑回归的假设函数 
带入上式时，我们得到的 
是一个非凸函数，如下图：
因此，此处我们需要重新考虑损失函数；
在逻辑回归中，我们最常用的损失函数为对数损失函数，对数损失函数可以为LR提供一个凸的代价函数，有利于使用梯度下降对参数求解。对数函数图像如图：
蓝色的曲线表示的是对数函数的图像，红色的曲线表示的是负对数
的图像，该图像在0-1区间上有一个很好的性质，如图粉红色曲线部分。在0-1区间上当z=1时，函数值为0，而z=0时，函数值为无穷大。这就可以和代价函数联系起来，在预测分类中当算法预测正确其代价函数应该为0；当预测错误，我们就应该用一个很大代价（无穷大）来惩罚我们的学习算法，使其不要轻易预测错误。
因此，我们重新定义逻辑回归的代价函数为：
损失函数的求解为：
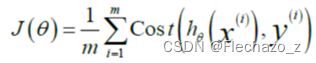
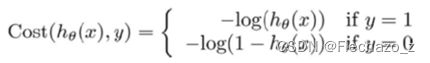
五、实验步骤
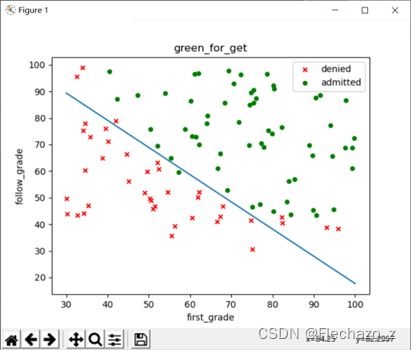
1. 数据可视化
在python中通过文件导入数据，并使用matlibplot工具建立对应散点图：
需要注意的是，我们的theta是三元组，θ0对应的X特征值固定为1，因此读取数据时，如上图最左侧加入一个1；
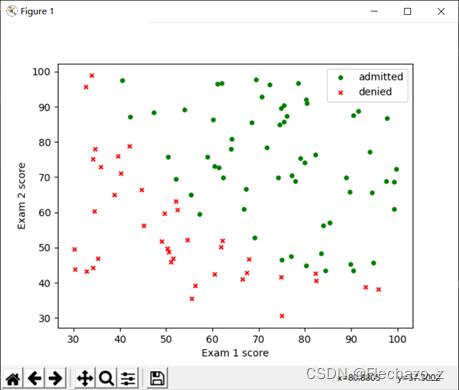
可以看到，被录取与不被录取的数据有较为清晰的一个界限，接下来我们要求解的就是这条界线；
2. 将线性回归参数初始化为0，计算代价函数(cost function)的初始值
根据基本原理中的代价计算公式，这里将sigmoid、损失公式代码化：
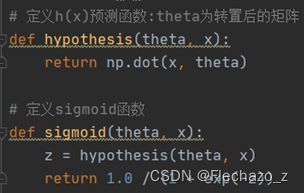
将theta初始化为（0，0，0）后，直接调用cost函数求值：
得到代价函数初始值：
3. 选择一种优化方法求解逻辑回归参数
3.1. 梯度下降法
我们选择先用梯度下降法来观察theta参数结果；
梯度下降算法代码实现如图：
X：对于线性回归中的常量b，我们可以将它的系数视为1，然后和变量x组成一个m行3列的矩阵，其中m是数据规模，这个矩阵就是X。
Y：一个m行1列的矩阵，对应是否录取。
alpha：学习率
第一步，将我们的Θ初始化为[[0][0][0]]。
第二步，对于给定的步长alpha和此时的梯度gradient，更新我们的theta。然后计算此时thrta对应的梯度更新gradient。
第三步，重复第二步30万次
第四步，返回theta，即为我们线性回归的参数。
但是，对于逻辑回归来说，这里遇到了一个问题，那就是alpha和迭代次数的取值，如果alpha过小，损失函数将收敛的非常慢，迭代次数达到40万时才勉强收敛，但如果alpha过大，又会导致过大的步长使得准确率下降；
alpha = 0.001时的收敛函数，在50万次时收敛： 0.005时在25万次时收敛；
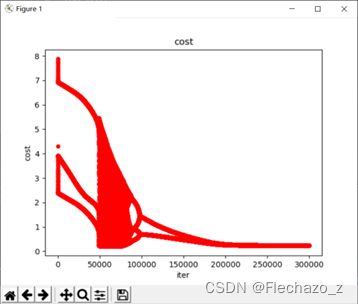
而如果alpha继续增大（如0.01），将导致不够准确，其界限与收敛图形如下：
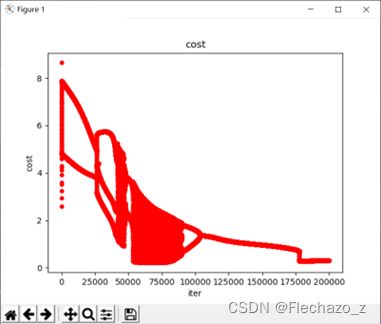
（界限太差，仅80%准确率，且需要20万次迭代）
因此，我们在运行该数据时需要运行稍长的时间；alpha=0.005，迭代次数为30万时可以得到一组回归参数：
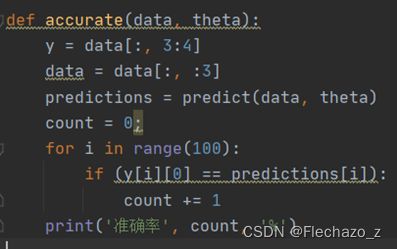
它的划分边界如图所示，其准确率为92%：该参数的划分准确率计算方法如下：
3.2. 牛顿迭代法
因为上述的迭代下降法所需迭代次数过多，因此这里使用一种优化方法来求解参数；
3.2.1. 方法介绍
牛顿迭代法的原理较为复杂，因此不在这里写出来。
对比这牛顿迭代法方法与梯度下降法的参数更新公式可以发现，两种方法不同在于牛顿法中多了一项二阶导数，这项二阶导数对参数更新的影响主要体现在 改变参数更新方向上。
如图所示，红色是牛顿法参数更新的方向，绿色为梯度下降法参数更新方向，因为牛顿法考虑了二阶导数，因而可以找到更优的参数更新方向，在每次更新的步幅相同的情况下，可以比梯度下降法节省很多的迭代次数。
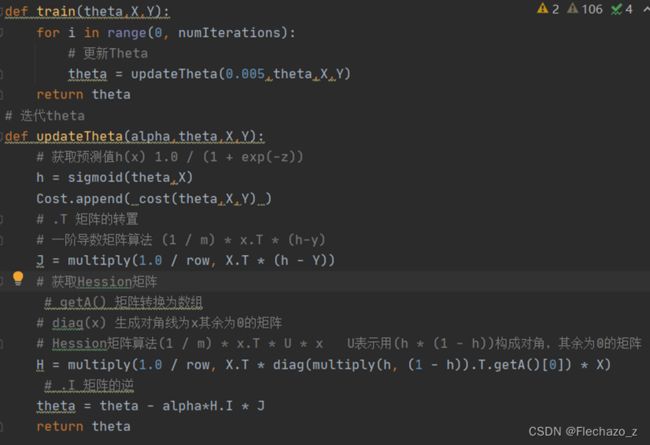
迭代过程：
3.2.2. 代码实现
h值为sigmoid函数求得的概率；
J为一阶偏导数
H为Hession矩阵（海塞矩阵），二阶偏导数
牛顿迭代法得到的theta：
3.2.3. 优点
对于同样的学习率alpha = 0.005，cost仅需要1000次迭代就差不多收敛了；
而如果放大alpha，如alpha = 0.5，那么它只需要迭代10次即可收敛。
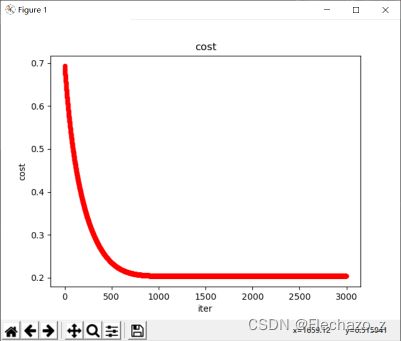
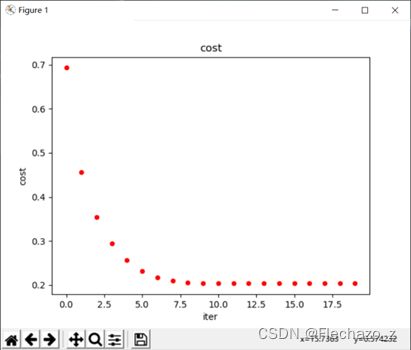
并且准确率保持在89%（数据较小）；
4. 某学生两次考试成绩分别为 42、85，预测其被录取的概率
这里直接使用sigmoid函数以及牛顿迭代法求得的theta来进行其概率的计算：
得到结果：
即，y=1的概率为0.65145509，也就是被录取的概率
5. 画出分类边界
在上面已经画出了梯度下降法的分类边界，这里给出牛顿迭代法的边界：
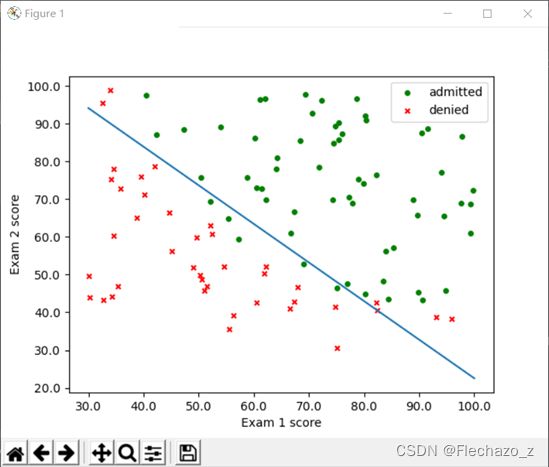
六、程序清单
LR_DE：梯度下降法的项目文件，程序都在main.py文件中；
LR_Newton：牛顿迭代法的项目文件，程序都在main.py文件中；
两个项目文件中均包含数据集