FPGA时序约束01——基本概念
前言
1. 越来越多的时序问题
随着FPGA时钟频率加快与其实现的逻辑功能越来越复杂,开发者遇到的问题很多时候不再是代码逻辑的问题,而是时序问题。一些开发者可能有这样的经历,一个模块在100MHz时钟运行没问题,而将时钟频率改为150MHz,模块功能就不正常了,这很可能就是整个系统的时序在150MHz下不满足要求,简言之,系统跑不到150MHz。
对于FPGA的设计,时序分析与约束正变得不可或缺,尽管有时FPGA只实现非常简单的功能,但仍可能遇到时序问题,如果缺乏基本的时序分析和约束能力,将在面对偶尔出现的“奇怪”现象时束手无策。
2. 时序分析的发展——动态时序分析与静态时序分析
动态时序分析是指在输入端输入一组向量,并观察信号到达电路中各个点的时间。通过了解所使用的输入和观察到的信号之间的时间差,我们就知道信号经过特定路径需要多长时间。对于触发器,通过观察输入D相对于输入CLK的到达时间,我们可以知道特定触发器是否满足建立和保持要求。因此,该过程依赖于时序仿真,也依赖于所施加的激励。
集成电路设计初期流程中,动态时序分析是一种非常流行的时序验证策略,但随着设计规模的增大,验证一个设计需要测试的向量的数量按指数级增长,而且这种方法难以保证足够的覆盖率。现存的仿真工具并没有足够的性能和能力对几百万门的设计进行完整的时序仿真。更大设计的出现以及庞大的向量集合使得动态仿真在设计流程中成为一个严重的瓶颈。上市时间的压力、芯片的复杂度、传统仿真器的仿真速度和计算能力上的限制都促进了时序分析技术从动态向静态迁移。
总得来说,动态时序分析已被淘汰,现在所说的时序分析指的都是静态时序分析。
静态时序分析,Static Timing Analysis,简称STA。STA的概念始于20世纪90年代中期,从那时起,它已经成为时序分析的首选方法。STA不依赖于输入向量,STA的内容包括分析电路拓扑并计算电路中不同信号到达各个点的时间窗口,然后将其与要求信号到达该点的时间进行比较。只要信号到达的时间范围满足要求,从STA的角度来看设计就是可用的。
STA的优点:
1)静态时序分析执行速度快。
2)静态时序分析不需要测试向量。
3)静态时序分析对于有时序路径的时序,测试覆盖率可以近乎达到100%。
4)静态时序分析能够完成动态仿真所不能实现的复杂分析。
STA的缺点:
1)静态时序分析不能验证设计的功能,设计功能验证还必须使用功能仿真来实现。
2)静态时序分析只能验证同步时序电路的时序特性,如果设计中含有较多的异步电路,则应该通过门级动态仿真来验证。
3)静态时序分析不能自动识别设计中的特殊路径,比如多周期路径(multi-cycle path)、非正常路径(false path)、多时钟分配关系(multiple clock)等,这需要设计者手动地通过时序约束文件来指导静态时序分析。
一. 建立与保持
1.1 建立分析
在STA中,建立是指在要求时间之前检查最新数据是否可用。因此,可以在任何终点进行建立检查——而不仅仅是触发器。即使在输出端也要进行建立检查。
建立可以用如下更通用的方式进行定义:数据需要在一些参考事件之前建立并使之可用。对于触发器,参考事件是时钟触发。对于其他终点,参考事件是“期望数据在那一点可用的时间”。
1.2 保持分析
类似地,保持是指在当前信号的稳定性要求满足之后,检查最新的数据可以干扰当前信号的最早时间。因此,像建立一样,可以在任何终点进行保持检查,包括在输出端——不仅仅是触发器。
保持可以用如下更通用的方式来定义:一些参考事件后,数据需要保持和不干涉。对于触发器,参考事件是时钟触发。对于其他终点,参考事件是“允许数据在此点变化的时间。”
1.3 其他分析
建立检查可以确保移动最慢的数据也能及时到达并满足建立的标准。因此,数据路径可以计算最大延迟。因此,它也称为最大分析(max analysis)。由于建立检查考虑了最晚到达的数据,所以也称其为晚期分析(late analysis)。
类似地,保持检查可以确保即使是移动最快的数据也不应该干扰其他数据,同时期望数据保持稳定。因此,数据路径计算最小延迟。因此,它也称为最小分析(min analysis)。由于保持检查考虑了最早到达的数据,所以也称其为早期分析(early analysis)。
STA的建立–保持分析也被称为最小–最大分析(min–max analysis)或早期–晚期分析(early–late analysis)。更重要的是熟悉这些概念,而不用太担心术语。有时,对同一个概念,不同的工具可能使用不同的术语。有时甚至使用相同的术语来指代不同上下文中的不同概念。
除了建立或保持分析之外,STA还进行脉冲宽度、恢复、撤销分析等。
1.4 建立时间
建立时间,steup time,写作 t s u t_{su} tsu,是指时序单元正常工作时,在功能上为了保证正确性,输入信号数据应该在时钟信号有效前到达并保持的最小时间。也就是说,数据至少要提前读取该数据的时钟边沿 t s u t_{su} tsu时间到达,才能被正确读取。
建立时间的测量值定义为:从数据信号的电压达到标准供电电压50%时间点到时钟信号电压达到标准供电电压50%时间点的时间间隔。如下图所示。
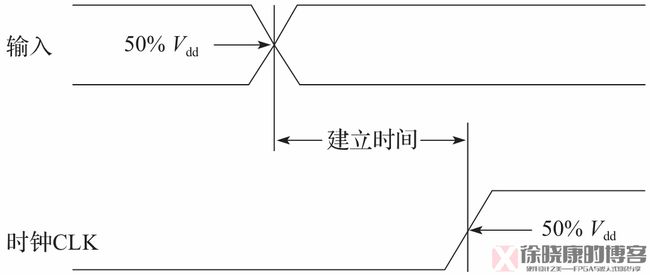
1.5 保持时间
保持时间,hold time,写作 t h t_h th,是指时序单元要实现正确的逻辑功能,数据信号在时钟沿有效后必须保持的最小时间长度。也就是说,数据至少要延后读取该数据的时钟边沿 t h t_h th时间,才能被正确读取。另一个说法是:下一个数据要来的慢一点,以便目的寄存器有足够的时间去读取上一个数据。
保持时间的测量值定义为:从时钟信号电压达到标准供电电压50%时间点到数据信号的电压达到标准供电电压50%时间点的时间间隔。如下图所示。

二. 时序路径
2.1 时序路径的起点和终点
**时序路径(timing path)**是指设计中数据信号传播过程中所经过的逻辑路径。每一条时序路径都存在与之对应的一个始发点和一个终止点,如下图所示。

从上图可知:
时序分析中定义的始发点可以分为两种:组合逻辑单元的数据输入端口和时序单元的时钟输入端口。
时序分析中定义的终止点也可以分为两种:组合逻辑单元的数据输出端口和时序单元的数据输入端口。
2.2 时序路径的分类
时序路径根据始发点和终止点的不同可分上图所示的4种类型:
- 触发器到触发器(register to register),表示始发点为时序单元的时钟输入端和终止点为数据输入端之间的时序路径。由于其始发点和终止点在设计内部都是可见的,所以也称为内部时序路径。
- 触发器到输出端(register to output),表示始发点为时序单元时钟输入端到终止点为组合逻辑单元的输出端之间的时序路径。由于组合逻辑单元的输出端口可能连接到设计之外的其他模块的输入端口,所以称为外部时序路径。
- 输入端到触发器(input to register),表示从始发点为组合逻辑单元的输入端到终止点为时序单元数据输入端之间的时序路径。由于组合逻辑单元的输入端口来自设计之外的其他输出端口,所以也称为外部时序路径。
- 输入端到输出端(input to output),表示从始发点为组合逻辑单元输入端到终止点为组合逻辑单元输出端之间的时序路径。因为没有经过任何时序单元,所以该种类型的时序路径比较特殊,其时序分析方法也不同。
三. 同步时钟
STA主要分析的就是同步时序,各触发器之间是共用一个时钟的,时钟是时序分析中最重要的信号。随着芯片工艺的提升,时钟频率越来越快,由时钟本身引起时序问题的现象越来越多,因此有必要了解和掌握高速时钟本身的时序特性,并且在静态时序分析过程中要把这些影响设计时序性能的时钟特性考虑进来。
时钟的时序特性主要分为时钟周期(clock period)、时钟占空比(clock duty cycle)、时钟转换时间(clock transition time)、时钟延迟(clock latency)、时钟偏斜(clock skew) 和 时钟抖动(clock jitter)。
3.1 时钟周期
时钟周期,clock period,也称为振荡周期,定义为时钟频率的倒数。STA中需要设置时钟周期即时钟信号的工作频率,作为时序参考基础,来检查时序路径是否满足时序要求。
3.2 时钟占空比
时钟占空比,clock duty cycle,是指时钟信号高电平在一个周期之内所占的时间比率,一般来说,占空比为50%,当然也可以根据需要设置成其它值。
3.3 时钟转换时间
时钟转换时间,clock conversion time。理想情况下,时钟信号在高低电平之间进行切换是不需要时间的,但是实际时钟信号在切换时,由于供电电压、工艺变化、扇出负载大小和互连负载大小等因素,是需要转换时间的。因此,时钟转换时间一般定义为时钟信号的电压从标准供电电源电压的10%变化到标准供电电源电压的90%的时间间隔,如下图所示。
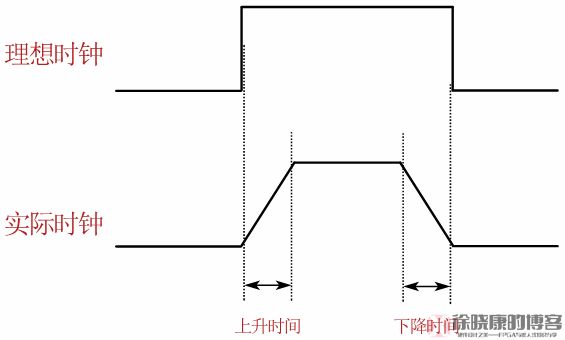
由于时钟转换时间分为上升和下降两种情况,应该使上升和下降转换的时间保持对称性。一般来说,时钟转换时间越短,上升和下降转换越对称,那么时钟信号质量越好。
3.4 时钟延迟
时钟延迟,clock delay,是指时钟信号从时钟源输出端口到达时序单元时钟输入端口所需要的传播时间,如下图所示。
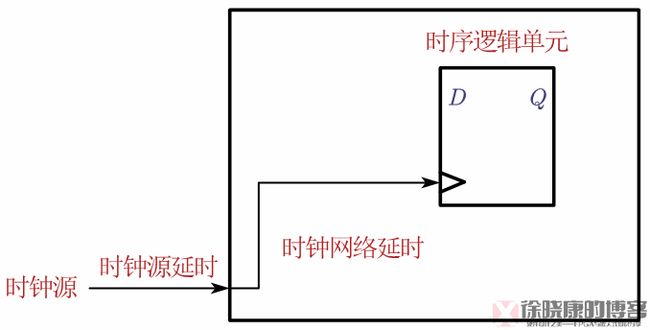
由于工艺、电压、温度等因素会不同幅度地影响时钟输入的延时,所以时钟输入延时具有不确定性。总的来说,时钟输入延时越短,时钟树性能越好。
3.5 时钟偏斜
时钟偏斜,clock skew,是指非理想情况下,由于时钟线长度及时钟树叶节点负载不同等因素,导致时钟信号到达同一时序路径下的相邻两个时序单元时钟端口的时间并不相同的现象。这种时钟信号之间的偏移就是相同时钟信号之间的时钟偏斜。
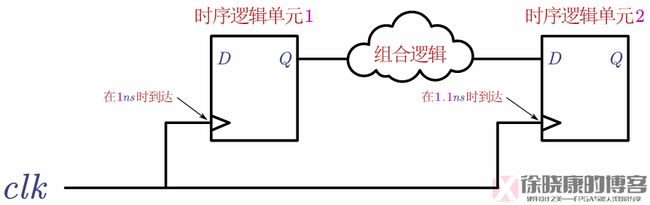
实际设计中,时钟信号到达每一个时序单元时钟端口的延时不可能完全相同,时钟偏斜是肯定存在的,这是时序分析中必须要考虑的因素。静态时序分析主要分为布局布线前和布局布线后两个阶段,两者的主要区别在于:后者有具体的互连线长度、宽度、信号分布情况等信息,所以后者可以更加准确地估计互连线延迟,以及时钟树网络的延迟;而前者只能根据设计电路和面积的大小等简单信息估计线上延迟和时钟树的延迟。
3.6 时钟抖动
时钟信号的上升沿在t1时刻发生,时钟周期为T,那么理想情况下,下一个时钟上升沿会在(T+t1)时刻发生,但实际情况是下一个时钟上升沿会略早于或者晚于这个时刻。在产生时钟的设备(如PLL)处,考虑到串扰、电磁干扰或PLL特性等因素时钟沿不具备确定性。这种时钟周期性的不良偏差称为抖动。这种偏移是在同一个时序单元的时钟输入端口上的时钟偏移,称为时钟抖动,如下图所示。

时钟抖动是永远存在的,该时钟抖动带来的影响在静态时序分析中可以通过设置时序裕度值来解决。
偏斜或抖动会导致不可预测性,即无法准确计算何时一个边沿能够到达触发器,这称为不确定度。
四. 裕量
裕量是指任何超出要求的额外的余地。
4.1 建立时间裕量
建立时间裕量,setup slack,写作slack(su),指的是实际数据提前数据要求时间到来的时间长度。
假设,时刻6之前要求信号可用(建立分析),而此信号在时刻4到达,那么信号有两个时间单位的建立时间裕量。
建立分析时,建立时间裕量的计算公式为:
建立时间裕量 s l a c k ( s u ) = 数据要求时间 − 数据到达时间 = d a t a r e q u i r a l t i m e ( s u ) − d a t a a r r i v a l t i m e ( s u ) \text{建立时间裕量}slack\left( su \right) =\text{数据要求时间}-\text{数据到达时间}=data\,\,requiral\,\,time\left( su \right) -\,\,data\,\,arrival\,\,time\left( su \right) 建立时间裕量slack(su)=数据要求时间−数据到达时间=datarequiraltime(su)−dataarrivaltime(su)
4.2 保持时间裕量
保持时间裕量,hold slack,写作slack(h),指的是下一个数据到达与上一个数据读取完成的时间间隔。
类似地,比如要求旧信号在时刻2之前保持稳定(保持分析),最早的一个新信号在时刻5到达那里,那么旧信号有3个时间单位的保持时间裕量。
保持分析时,保持时间裕量的计算公式为:
保持时间裕量 s l a c k ( h ) = 下一个数据的到达时间 − 此数据的读取要求时间 = d a t a a r r i v a l t i m e ( h ) − d a t a r e q u i r a l t i m e ( h ) \text{保持时间裕量}slack\left( h \right) =\text{下一个数据的到达时间}-\text{此数据的读取要求时间}=data\,\,arrival\,\,time\left( h \right) -data\,\,requiral\,\,time\left( h \right) 保持时间裕量slack(h)=下一个数据的到达时间−此数据的读取要求时间=dataarrivaltime(h)−datarequiraltime(h)
五. 一个时序分析的例子
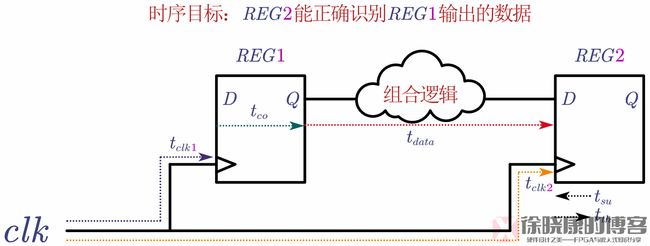
其中,
-
REG1,REG2表示两个寄存器,D为数据输入端,Q为数据输出端。
-
clk为两寄存器共用的时钟,对于FPGA来说,clk有三个来源:1. 外部时钟引脚;2. PLL输出;3. 门控时钟输出。
-
t c l k 1 t_{clk1} tclk1为clk传递到REG1的时钟端口的延时, t c l k 2 t_{clk2} tclk2为clk传递到REG2的时钟端口延时。
-
t c o t_{co} tco,clock output delay,寄存器数据输出延时,指的是时钟边沿有效后,还需要多长时间Q端输出才有效。
-
t d a t a t_{data} tdata,data delay,数据传输延时,指的是数据从源寄存器Q端输出到目的寄存器D端需要的时间。
-
t s u t_{su} tsu,建立时间。
-
t h t_{h} th,保持时间。
根据分析画出时序图如下:

建立时间裕量分析:

保持时间裕量分析:

六. 参考
-
《集成电路静态时序分析与建模》刘峰 编著,第一章与第二章。
-
《综合与时序分析的设计约束:Synopsys设计约束(SDC)实用指南 Constraining Designs for Synthesis and Timing Analysis (美)斯里达尔·甘加达兰(Sridhar Gangadharan)等著,韩德强 等译,第三章。
FPGA初学,写的比较浅,如有错漏,欢迎指出!
徐晓康的博客持续分享高质量硬件、FPGA与嵌入式知识,软件,工具等内容,欢迎大家关注。