通用对抗样本 Universal Adversarial Example

Universal Adversarial Example介绍

对抗样本（Adversarial Example）是近年来机器学习领域比较火的研究话题，这类样本可以说是机器学习模型的死敌，可以让目前性能最好的机器学习模型都丧失其分类能力
本文旨在介绍更为特殊的一类对抗样本——通用对抗样本Universal Adversarial Example。

通用对抗样本的定义

对于样本$x\in X$，机器学习模型$f(x)$，找到一个扰动$v$，使得 ¹：$$f(x+v)\ne f(x),foralmostallx\in X\text{\hspace{1em}(1)}$$
满足上式的扰动$v$被称为通用对抗扰动。因为$v$对于大部分样本都有效，因此危害性比一般的对抗扰动危害性更大，表现在两个方面：
（1）基于通用对抗扰动的攻击在测试阶段不需要目标模型的任何信息；
（2）极大地降低了实施对抗攻击的门槛，有效的话会在攻击者之间迅速流传。

生成通用对抗样本

目前，求解优化问题（1）主要采取迭代的方式，本文就以Universal adversarial perturbations²这篇论文为例进行介绍，这篇论文第一次发现了通用对抗扰动的存在。Algorithm 1 显示了生成通用对抗扰动的伪代码，其中$X$表示数据集，$\hat{k}$表示目标模型（被攻击的模型），$\xi$表示扰动向量$v$被允许的最大模长（$\xi$越大攻击的成功率越高，但是对抗样本与原始样本的差别或距离越大），$\delta$表示期望的目标模型的准确率。

Step 3：初始化对抗扰动$v$为零向量；
Step 4-10：对于$x_i\in X$，为样本$x_i+v$找到对抗性扰动$v$（使用白箱攻击算法deepfool进行求解，deepfool在Python对抗攻击库foolbox里面有实现）。就这样不断更新$v$，直到目标模型的准确率低于$1-\delta$。

图解通用对抗样本

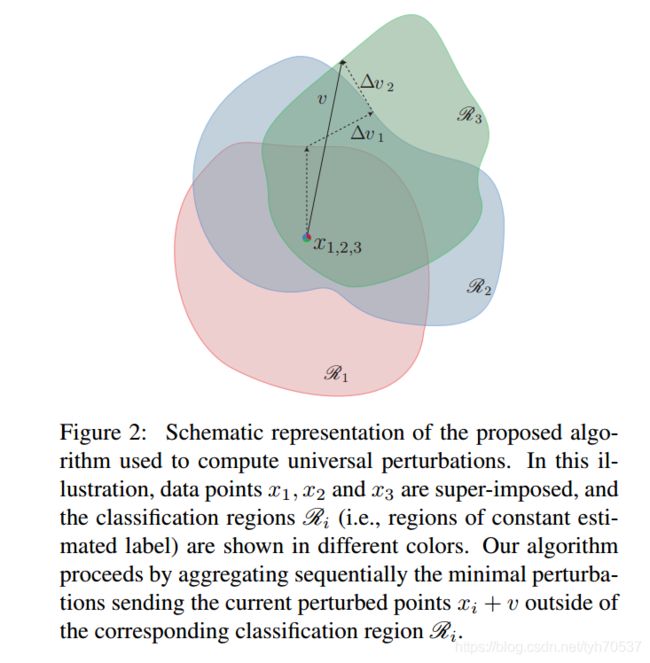
下图显示了通用对抗样本的生成过程，图中相同颜色区域内目标模型的分类结果不变，为了方便说明生成过程。作者选取的三个样本$x_1,x_2,x_3$是叠加在一起的，即$x_1=x_2=x_3$。
首先，$x_1$被加上一个扰动$\Delta v_0$（图中没显示），移动到红色区域的边界上；
接着，$x_2+\Delta v_0$被加上扰动$\Delta v_1$，移动到蓝色边界上；
最后，$x_3+\Delta v_0+\Delta v_1$被加上扰动$\Delta v_2$，移动到蓝色边界上。
$v=\Delta v_0+\Delta v_1+\Delta v_2$就是我们要的通用对抗扰动。

代码

# -*- coding: utf-8 -*-
"""
Created on Wed May 12 21:04:46 2021

@author: coco
"""
from filename import *
import numpy as np
import foolbox #2.4版本
from tensorflow.keras.utils import to_categorical
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import Dense

def DNN_clc(X_tr,y_tr):
    '''
    训练一个简单的目标模型
    '''
    y_ = to_categorical(y_tr)
    model = Sequential()
    model.add(Dense(36, input_shape=(X_tr.shape[1],), init='uniform', activation='relu'))
    model.add(Dense(36,  activation='relu'))
    model.add(Dense(36,  activation='sigmoid'))
    model.add(Dense(2,  activation='softmax'))
    model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
    model.fit(X_tr,y_,batch_size=5,epochs=30)
    return model

def norm(v,p):
    '''
    该函数将超出最大长度的对抗扰动v映射回允许的范围，计算方式是经过推导得到的，保证v的模长为p
    v:规范前的扰动向量
    p:对抗扰动的最大模长
    
    '''
    h = np.sum(v*v)/(p**2)
    if h < 1:  
        print('v还小')
        '''
        当前的没有超出长度限制
        这种情况下不需要进行改变
        '''
        return v 
    else:        
        Lambda = (h)**0.5 - 1
        x = v/(1 + Lambda)
        return x
def UAP(X, y, targetModel, rho):
    '''
    X:白箱攻击, 因此可以使用全部的训练集
    y:类别标签
    rho:攻击强度
    '''
    model = targetModel #目标模型
    fmodel = foolbox.models.KerasModel(model, bounds=(0, 1)) #注意样本是归一化，取值在0和1之间
    attack  = foolbox.v1.attacks.DeepFoolL2Attack(fmodel)
    X_P = X[np.where(y==1)] #训练集中全部的正类样本

    v = np.zeros(len(X[0])) #初始化对抗扰动
    for j in range(len(X_P)):
#        print("j:",j)
        new_p = np.clip(X_P[j]+v,0,1) #防止样本超出边界
        adv = attack.__call__(input_or_adv=new_p, label=1, steps=500)
        if adv is None:
            print('出现空值')
        else:   
            perturbation = adv - X_P[j] -v
            if sum(perturbation)==0:
                print('已经是对抗样本')
            else:
                v = v + perturbation
                v = norm(v,p=rho)
    return v

Data = np.loadtxt('german.txt') #数据集，我用的是二分类面板数据，最后一列是类别标签
scaler = MinMaxScaler() 
scaler.fit(Data)
Data = scaler.transform(Data) #数据归一化
X, y = Data[:,:-1], Data[:,-1]  #数据集的特征和类别
model = DNN_clc(X, y)  #keras目标模型神经网络
UAP_v = UAP(X, y, model, 1) #通用对抗扰动,专门针对正类样本

X_P = X[np.where(y==1)] #原始的正类样本
adv = X_P + UAP_v #对抗样本
print('目标模型对于原始正类样本的准确率:', np.sum(model.predict_classes(X_P))/len(X_P)) 
print('目标模型对于对抗样本的准确率:',np.sum(model.predict_classes(adv))/len(X_P))

代码我这里跑的通，记得用Python3、foolbox2.4版本，foolbox3版本不支持keras。

---

1. Chaubey, Ashutosh, et al. “Universal adversarial perturbations: A survey.” arXiv preprint arXiv:2005.08087. 2020. ↩︎

2. Moosavi-Dezfooli, Seyed-Mohsen, et al. “Universal adversarial perturbations.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2017. ↩︎