机器学习笔记：Support Vector Machine

基本知识点

1.Linear SVM with Hard Margin

SVM是一种二元分类器，其基本思想也是基于训练样本找到能够将两类样本分开的划分超平面/决策边界。首先，以线性SVM为例，其模型形式如下：

$$f_{w,b}(x)=w^{T}x+b$$

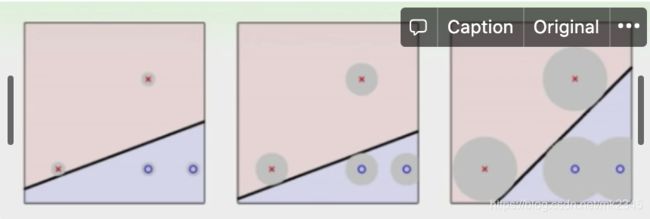
然而划分样本的决策边界可能有很多条，应该挑选具有什么特质的决策边界，SVM给出的答案是，挑选一条边界，使其间隔（margin）最大化，如图所示：

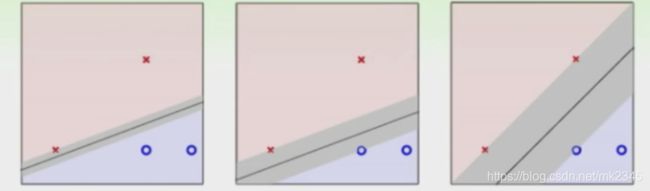
从上图，可以直观地感受到，最右图的决策边界相较左边两幅图要更加稳定一点，因为每个样本可以辐射的灰色区域更大一些，也就意味着它可以容忍的“误差”要更大一些。假使有一个模型没见过的样本，它属于红类，显然在最右图其落在红类灰色区域的概率要远比左边两幅图大，那么它被正确判断为红类的概率也就比左边两幅图大。图中两个异类样本到该直线的最短距离之和，被称作**间隔，**下图直观地展示了间隔的含义：

换言之，满足间隔最大化的这一条边界，其产生的分类结果是最稳定的，对未见样本的泛化能力也就最强。

**在SVM中，正类值为1，负类值为-1，**如果决策边界可以将训练样本正确分类 ，则有：

$$\{\begin{array}{ll}{w}^T{x}_i+b\ge 1& \text{if }{y}_i=1\\ w^T{x}_i+b\le -1& \text{if }{y}_i=-1\end{array}$$

同时，样本点与决策边界的距离有公式如下：

$$d=\frac{|w^T{x}_i+b|}{||w||}$$

那些使$w^T{x}_i+b$的等号成立的样本点，也就是距离决策边界最近决定了间隔大小的样本点，有公式如下：

$$\begin{gathered} d=\frac{1}{||w||} \\ margin=2d=\frac{2}{||w||} \end{gathered}$$

对以上式子做一些小小的改动，最终写出**SVM的原型（目标函数以及约束条件）**如下：

$$\begin{gathered} mi{n}_{w,b}\frac{1}{2}||w|{|}^2 \\ st.y_i(w^T{x}_i+b)\ge 1 \end{gathered}$$

实际上，在测试集上应用SVM时，当$w^T{x}_i+b>0$就可以判断其为正样本，在训练集上约束条件设置为$w^T{x}_i+b\ge 1$，是一种缩放变换，**具体证明过程可参考林轩田关于SVM问题的视频讲解**。（可以直接尝试理解成，为了使margin的极值优化问题变得更加简单，直接将$w^T{x}_i+b$设置为1，约束条件中的$w^T{x}_i+b>0$也将随之同步变为$w^T{x}_i+b\ge 1$；也可以认为，这个公式的目的就在于就是设置margin成为一个不为0的数，从而使得SVM能够去选择一个有间隔、表现更稳定的决策边界。）

以上就是线性SVM模型针对最大化间隔问题所给出的解决方案，它是一个线性规划的凸函数问题，也就是说它一定有一个可以通过数学方式直接求得的最优解。

然而，SVM原型的约束条件十分绝对，在现实任务中，很难找到一条完全满足上述公式的决策边界，即使存在，这样绝对的约束条件也很容易导致过拟合现象的产生，为了缓解这个问题，需要在SVM原型中引入“软间隔”的概念。

2.Linear SVM with Soft Margin

在第一部分中，SVM原型要求所有样本必须满足约束条件$y_i(w^T{x}_i+b)\ge 1$，这实际上是一种**“硬间隔SVM“，反之，“软间隔”就是指允许一些样本不满足约束条件。软间隔SVM的核心思想就是，在最大化间隔的同时使不满足约束条件的样本尽可能少，设样本量为m，这个思想可以被量化成最小化软间隔SVM的loss function，**如下：

$$minL(w,b)=min\frac{1}{2}||w|{|}^2+C\sum _{i=1}^{m}max(0,1-y_i(w^T{x}_i+b))$$

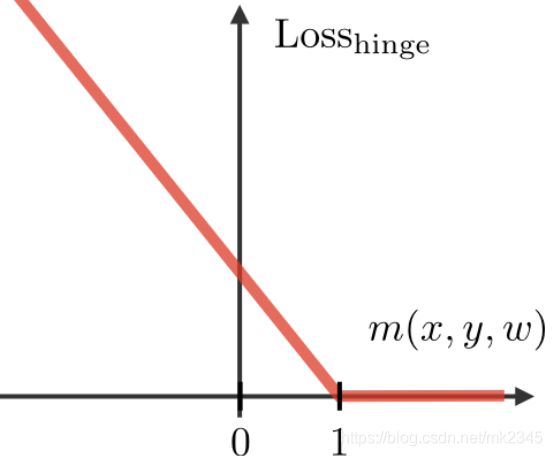
其中，$max(0,1-y_i(w^T{x}_i+b))$是一个合页损失函数（hinge loss function），在SVM中相当于一个松弛变量（slack variable），它的图像如下：

直观来看，当$y_i(w^T{x}_i+b)\ge 1$，样本满足约束条件时，hinge loss就为0，当$y_i(w^T{x}_i+b)<1$时，样本不满足约束条件时，hinge loss就是$1-y_i(w^T{x}_i+b)$本身。可以这样理解，hinge loss是一个**“不关心样本有多正确，只关心样本有多错误”的loss function，所以，如果有一个十分正确的样本，SVM的loss function在优化过程中就不会再把它考虑在内，而只会去考虑还没有被分类正确的样本，这些没被正确分类样本的特征向量就是支持向量。**

如果从数学的角度来看，考虑一个梯度下降的优化过程（假设只有一个样本参与），那么权值更新的过程如下：

$$\begin{gathered} w_i=w_i-\eta \frac{\partial L(w,b)}{\partial w_i}=w_i-\eta w_i-\eta \frac{\partial L(w,b)}{\partial f(x_i)}\frac{\partial f(x_i)}{\partial w_i} \\ =w_i-\eta w_i-\eta \frac{\partial max(0,1-y_{i}f(x_i))}{\partial f(x_i)}{x}_i \end{gathered}$$

其中：

$$\frac{\partial max(0,1-y_{i}f(x_i))}{\partial f(x_i)}=\{\begin{array}{ll}-y_i& \text{if }{y}_{i}f(x_i)<1\\ 0& \text{otherwise }\end{array}$$

从上式也可以看出，当一个样本被正确分类后，它在权值更新过程中就没有任何作用，对最终求得的最优解没有任何贡献，所以hinge loss的使用确保了SVM解的稀疏性，即使噪音多，也不会影响软间隔SVM最终求得的结果。

3.SVM with Kernel

以上两部分，均是在决策边界为线性的SVM基础之上进行讨论，然而大多数时候分类任务可能会需要模型去寻找一个非线性的决策边界，此时就需要通过核函数将特征向量映射到高维空间去寻找一个可以划分不同类别的超平面，Kernel SVM的模型形式如下 ：

$$f_{\alpha }(x)=\sum _{i=1}^m{\alpha }_{i}K(x_i,x)$$

其中，$K(x_i,x)$为核函数，有高斯核函数、线性核函数（当核函数为线性时，Kernel SVM就是Linear SVM）、多项式核函数等可供选择 。$f_{\alpha }(x)$的思想就是，首先通过核函数计算一个特征向量跟所有特征向量在高维空间的相似度，再通过$\alpha$加权得到最终的结果（即该样本靠近哪一类）。在这其中，核函数承担了特征映射以及相似度计算这两个任务，简单考虑一个多项式核函数，有如下公式成立：

$$K(x_i,z)=(x_i\cdot z{)}^2=\varphi (x_i)\cdot \varphi (z)$$

• 此处的具体证明可以参见李宏毅老师的课程讲解，课件展示如下：
  

其中，$x_i\cdot z$是向量的内积，内积越大，两个向量相似度越高。上式告诉我们，**先对$x_i$和$z$求相似度再经过核函数映射到高维空间与先将$x_i$和$z$映射到高维空间再对其进行相似度计算是等价的，**所以，只要选定一个核函数，就可以完成特征向量在高维空间的相似度计算，而不需要人为去考虑映射的具体形式，通过具体形式转换向量后再求取相似度（因为人为确定具体形式是一件比较难的事，且先确定具体形式再计算相似度会增加不必要的复杂度）。

在对核函数的选择上，最常用的核函数为高斯核函数：

$$K(x,z)=exp(-\frac{||x-z|{|}^2}{2{\sigma }^2})$$

该学习笔记是在综合了李宏毅、吴恩达、林轩田、周志华等大佬的讲解后记录下来的。