AES缓存碰撞攻击在美国太空安全挑战赛中的应用

       国家太空安全是国家安全在空间领域的表现。随着太空技术在政治、经济、军事、文化等各个领域的应用不断增加，太空已经成为国家赖以生存与发展的命脉之一，凝聚着巨大的国家利益，太空安全的重要性日益凸显。而在信息化时代，太空安全与信息安全紧密地结合在一起。2020年9月4日,美国白宫发布了首份针对太空网络空间安全的指令——《航天政策第5号令》，其为美国首个关于卫星和相关系统网络安全的综合性政策，标志着美国对太空网络安全的重视程度达到新的高度[1]。随后美国空军组织了“黑一颗卫星（Hack A Sat）”[2]太空安全挑战赛，该赛事涵盖多个领域的知识，本文使用AES缓存碰撞攻击给出了该赛事其中一个挑战的解决方案。

1 美太空安全挑战赛介绍

       从2020年起，美国空军已经连续两年举办太空安全挑战赛。该赛事分为资格赛、决赛两个阶段，资格赛采用积分制，资格赛中积分前8名的参赛队进入决赛，最终角逐出前三名。以2021年为例，在6月26日至27日为期30小时的资格赛中，有75个以上国家近3000名竞争对手组成的1000多支队伍参加。资格赛由5个类别的24个挑战组成，侧重于不同的技能组合，包括卫星操作、逆向工程和射频通信等。12月11日至12日决赛期间，8个团队参加了持续24小时的决赛，决赛项目是攻防对抗式的夺旗赛，包括争夺虚拟地面站、通信子系统、“平卫星”物理卫星硬件，以及用于模拟和测试命令的数字孪生软件。各团队被要求同时操作和防御自己具有脆弱性的系统，同时攻击对手相同的系统来得分。系统中存在许多可利用的漏洞，团队必须修补或以其他方式减轻自己漏洞所产生的影响，以防止系统被攻击，同时保持系统正常运行[3]。

        在2020年第一届太空安全挑战赛中，在“载荷模块（Payload Module）”这个类别下有一个挑战是“密码泄露（Leaky Crypto）”，主办方给出的挑战信息如下：

      有一颗卫星在通信过程中，会对每个消息使用ECB（Electronic Codebook；电码本）模式的AES-128（Advanced Encryption Standard；高级加密标准）算法[4-6]进行加密。攻击者由于不知道密钥，无法正常加密，那么当攻击者向卫星发送消息后，卫星就会发现消息不对，从而丢弃该伪造消息。攻击者已经截获了一段密文，需要参赛者给出对应的明文，并且已知如下一些信息：

（1）知道密钥的前6个字节是“0xc35c7a9947fe”。

（2）知道截获密文对应明文的前几个字节是“flag{ksjkglhwsjd”。

（3）提供了100000行尝试攻击数据，每个数据包括两部分：明文、加密明文时间，部分数据如下所示。

ed74cd51ab28e765d1e98965e86ba749,10584

ea0c914e1ff97edbe3bd46228f53771e,10656

3e8d4ed226d2ffea86fcf8be22af3e33,10704

3bd7f7bb63745fc45940220e417a116d,10632

99c5843576a344f0d8ec990795912a38,10632

34239b24eef47313a14e0a55767810dd,10632

7b9ae4bdb410862d12de1d94cd40853a,10656

f54c322e63f3b169fdfb4b161decc9b6,10680

91359a6820ecadafd2e616aa2c0baa42,10680

c4ce053a2df7f883d24905856df2b180,10656

       从给出的挑战信息可知，这是已知加解密算法、部分明文、全部密文，并且有大量明文及其加密时间的数据，要求得出加密密钥的挑战。本文利用AES缓存碰撞攻击方法给出解决方案。

2 AES加密过程介绍

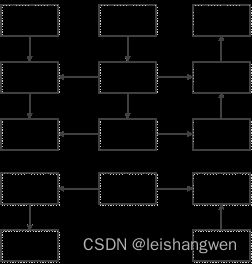
        AES是美国联邦政府采用的一种区块加密标准，是一种对称加密算法[7-8]，对称加密即加密与解密用的是同样的密钥。AES因其运算速度快、安全性高的优点，用来替代原先的DES（Data Encryption Standard；数据加密标准），已经被广泛使用[9-12]。其加密、解密基本过程如图1所示，左边是加密过程，右边是解密过程，加密、解密是对称的。从图中可以发现，加密、解密需要进行多轮计算，密钥长度不同，导致计算轮数不同，根据密钥长度不同AES分为AES-128、AES-192[13]、AES-256[14]。对于AES-128，加密、解密过程有10轮运算。

图1 AES加密、解密基本过程

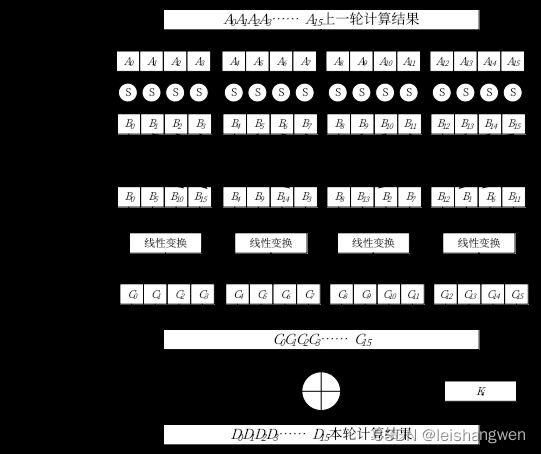
         其中每一轮运算的过程如图2所示。每一轮对16个字节进行运算，由四层组成：字节代换层（Byte Substitution Layer）、ShiftRows层、MixColumn层、密钥加法层（Key Addition Layer）。

图2 AES每一轮的运算

       AES在软件层面和硬件层面都已经有了很多种实现方式。其中AES设计者提议的一种快速软件实现——查表法得到广泛应用。查表法的核心思想是将字节代换层、ShiftRows层和MixColumn层融合为查找表，每个表的大小是256条，每一条是4字节，一般称为T盒（T-box）或T表。加密过程4个表（Te），解密过程4个表（Td），共8个。每一轮操作都通过16次查表产生。虽然一轮就要经历16次查表，但这都简化了伽罗瓦域（Galois field）上的计算操作和矩阵乘法操作，而且T表一般提前编写程序算出，然后作为一个常量数组，硬编码在AES的软件实现代码中，对于计算机而言是非常简单高效的查表和按位运算。于是，每一轮的计算可以使用公式(1)表示。从公式(1)中可以发现，查找A0、A4、A8、A12的时候使用的都是Te0表，查找A5、A9、A13、A1的时候使用的都是Te1表，查找A10、A14、A2、A6的时候使用的都是Te2表，查找A15、A3、A7、A11的时候使用的都是Te3表，将使用同一个Te表的那4个字节称为一个家族（family）。

3 AES缓存碰撞攻击原理

        假设明文为P，大小为16字节，第i个字节为Pi，密钥为K，大小也为16字节，第i个字节为Ki，对于第一轮计算，查找表的序号是Pi⊕Ki，如表1所示。假如P0⊕K0等于P4⊕K4，那么这两次查表将查找到的是同一个内存地址，根据处理器的工作原理，由于已经将P0⊕K0对应的数据从内存读取到了缓存，所以再次读取P4⊕K4对应的数据的时候，将直接从缓存读取对应数据，时间将大大节省。如果出现这种情况，那么由于已知P0、K0、K4，就可以计算得到对应的P4。[15]

表1 第一轮查找表的序号

T表	Te0	Te1	Te2	Te3
序号	P0⊕K0	P5⊕K5	P10⊕K10	P15⊕K15
	P4⊕K4	P9⊕K9	P14⊕K14	P3⊕K3
	P8⊕K8	P13⊕K13	P2⊕K2	P7⊕K7
	P12⊕K12	P1⊕K1	P6⊕K6	P11⊕K11

       从挑战赛题目可知，目前有100000组明文数据，其中有每一组明文数据的加密时间，并且已知密钥的前6个字节，根据上述原理，尝试使用密钥的第0字节，推测密钥的第4字节，以验证上述分析是否成立。验证步骤如下：

（1）对100000组数据，每一组数据的第0字节与已知密钥的第0字节进行异或运算，得到结果数组Set0；

（2）假设密钥第4个字节为x，那么对100000组数据，每一组数据的第4字节与x进行异或运算，得到结果数组Set1；

（3）对比Set0、Set1，可以得到其中相同的元素的序号集，这个序号集称为碰撞数据集CollisionSet，不相同的元素的序号集称为非碰撞数据集non-CollosionSet；

（4）将测试数据中，non-CollosionSet中对应明文的加密时间取一个均值non-CollosionSetMeanTime，将测试数据中，CollisionSet中对应明文的加密时间取一个均值CollosionSetMeanTime；

（5）将non-CollosionSetMeanTime减去CollosionSetMeanTime，得到一个时间差；

（6）对于密钥第4字节的所有256种可能值，重复第2-6步，得到256个时间差；

（7）取出时间差绝对值最大的前10个对应的猜测值，其中应有密钥第4字节对应的值。

        按照上述步骤，编写程序，得到时间差的情况如图3所示，其中横轴是密钥第4字节的0-255可能的值，纵轴是计算出来的时间差，可见有一个明显的峰值，表示时间差很大。时间差最大的前10个可能值如下：

70  69  68  71  187  133  179  105  96  180

       从挑战题目给出的已知密钥可知，密钥的第4字节是0x47（十进制为71），正是在上述推测出来最有可能的10个值中，因此，可以证明AES缓存碰撞攻击可以用于本挑战的解答。

图3 当密钥第4个字节依次取0-255时，分别对应的加密时间差

4 AES缓存碰撞攻击实现

将上述推测密钥第4字节的过程称为密钥推测函数KeySearch，其函数定义原型如下：

def keysearch(l_ref, targets): 

其中，l_ref是已知密钥的某个字节，由这个字节推测与这个字节在一个family中的其余字节。已知密钥的前6个字节，所以可由密钥第0字节推测第4、8、12字节，由密钥第1字节推测密钥第5、9、13字节，由密钥第2字节推测密钥第6、10、14字节，由密钥第3字节推测密钥第7、11、15字节；由密钥第4字节推测密钥第8、12字节；由密钥第5字节推测密钥第9、13字节。

keysearch(l_ref_0, [4,8,12])

keysearch(l_ref_4, [0,8,12])

keysearch(l_ref_1, [5,9,13])

keysearch(l_ref_5, [1,9,13])

keysearch(l_ref_2, [6,10,14])

keysearch(l_ref_3, [7,11,15])

第一轮推测结果如下，此处只取了前四个最有可能的结果。

Found candidate values for key byte 8

[38 37 36 39]

Found candidate values for key byte 9

[235 234 233 232]

Found candidate values for key byte 14

[31 29 28 30]

Found candidate values for key byte 7

[31 30 29 28]

Found candidate values for key byte 15

[155 154 152 153]

可知，推测出了密钥第7、8、9、14、15字节的可能值。还有密钥第6、10、11、12、13字节没有推测出来。继续使用推测出来的新的字节推测未知字节，如下：

keysearch(l_ref_7, [11])

keysearch(l_ref_8, [12])

keysearch(l_ref_9, [13])

keysearch(l_ref_14, [6,10])

keysearch(l_ref_15, [11])

第二轮推测结果如下，此处只取了前四个最有可能的结果。

Found candidate values for key byte 13

[220 221 223 222]

Found candidate values for key byte 10

[50 48 51 49]

可知，新推测出了密钥的第10、13字节的可能值。还有密钥第6、11、12字节没有推测出来。继续使用推测出来的新的字节推测未知字节，如下：

keysearch(l_ref_10, [2,6,14])

第三轮推测结果如下，此处只取了前四个最有可能的结果。

Found candidate values for key byte 14

[31 29 30 28] 24.61651797495142

可知，只是推测出了密钥第14字节的可能值，而这个结果前文已经得到了，所以密钥第6、11、12仍然还没有推测得到。这里将family的范围扩大，用密钥的任一字节使用keySearch推测其余15个字节的值。

keysearch(l_ref_0, range(16))

keysearch(l_ref_1, range(16))

keysearch(l_ref_2, range(16))

keysearch(l_ref_3, range(16))

keysearch(l_ref_4, range(16))

keysearch(l_ref_5, range(16))

keysearch(l_ref_7, range(16))

keysearch(l_ref_8, range(16))

keysearch(l_ref_9, range(16))

keysearch(l_ref_10, range(16))

keysearch(l_ref_13, range(16))

keysearch(l_ref_14, range(16))

keysearch(l_ref_15, range(16))

第四轮推测结果如下，此处只取了前四个最有可能的结果。

Found candidate values for key byte 12

[150 148 149 151] 25.77075236406381

Found candidate values for key byte 6

[13 14 15 12] 25.987920521583874

可知，推测出了密钥第6、12字节的值，现在只剩下第11字节还没有推测结果。但是整个解空间大小减少为，因为已知部分明文，就可以使用暴力破解法，通过穷举所有的可能性对挑战赛给出的密文进行解密，对比已知的部分明文，最终确定正确的密钥。本文使用Intel i7-10750H处理器，32G内存的计算机最终暴力破解使用了9分21秒。

以上摘自《Hack-A-Sat太空信息安全挑战赛深度解析》一书

[1]苟子奕, 韩春阳. 美国太空领域的网络安全政策分析[J]. 国际太空, 2021(1):5.

[2]Hack a sat https://www.hackasat.com/

[3]星际智汇.美空军部宣布“黑一颗卫星”挑战赛冠军【太空军事化】美空军部宣布“黑一颗卫星”挑战赛冠军，2021.12.16

[4] Bahrak B, Aref M R. Impossible differential attack on seven-round AES-128[J]. IET Information Security, 2008, 2(2): 28-32.

[5] Liberatori M, Otero F, Bonadero J C, et al. Aes-128 cipher. high speed, low cost fpga implementation[C]//2007 3RD Southern Conference on Programmable Logic. IEEE, 2007: 195-198.

[6] Almazrooie M, Samsudin A, Abdullah R, et al. Quantum reversible circuit of AES-128[J]. Quantum Information Processing, 2018, 17(5): 1-30.

[7]吕慧,赵跃华. 基于掩码的 AES 算法抗二阶 DPA 攻 击方法研究 [J]. 电子设计工程,2015,23(20):31 - 33.

[8]黄灿英,汪莹,陈艳. 基于AES-128密码算法的嵌入式系统安全[J]. 沈阳工业大学学报,2020(5). DOI:10.7688/j.issn.1000-1646.2020.05.13.

[9]卢军,张国辉,李国强. 一种基于数据分解的 AES 优化算法设计 [J]. 单片机与嵌入式系统应用,2019, 19(4):22-25.

[10]万刘蝉,韦永壮. AES-128 的密钥中比特检测及分析 [J]. 桂林电子科技大学学报,2016,36(4):338 - 341.

[11]Tsai K L,Huang Y L,Leu F Y,et al. AES-128 based secure low power communication for LoRaWAN IoT environments [J]. IEEE Access,2018,6:51 -66.

[12]Mahajan P, Sachdeva A. A study of encryption algorithms AES, DES and RSA for security[J]. Global Journal of Computer Science and Technology, 2013.

[13] Han L, Wu N, Ge F, et al. Differential Fault Attack for the Iterative Operation of AES-192 Key Expansion[C]//2020 IEEE 20th International Conference on Communication Technology (ICCT). IEEE, 2020: 1156-1160.

[14] Biryukov A, Dunkelman O, Keller N, et al. Key recovery attacks of practical complexity on AES-256 variants with up to 10 rounds[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer, Berlin, Heidelberg, 2010: 299-319.

[15]Bonneau J ,  Mironov I . Cache-Collision Timing Attacks Against AES[C]. International Workshop on Cryptographic Hardware and Embedded Systems. Springer, Berlin, Heidelberg, 2006.