【数值分析】Jacobi、Seidel和Sor迭代法求解线性方程组（附matlab代码）

线性方程组迭代解法公式类似非线性方程求根的简单迭代法公式， 有Jacobi迭代法、 Seidel迭代法及Sor法等。

题目1-Jacobi迭代法和Seidel迭代法

来源：《数值分析》第5版，清华大学出版社，作者：李庆扬等，第6章习题1

代码1-Jocabi

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 简介：用Jocabi迭代法求解线性方程组，要求误差小于10^(-4)
% 作者：不雨_亦潇潇
% 文件：Jocabi.m
% 日期：20221102
% 博客：https://blog.csdn.net/weixin_43470383/article/details/127661516
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc; clear all;
x_10 = 0;
x_20 = 0;
x_30 = 0;
n = 0;
err = 1;

while err>10^(-4)
    x_11 = -0.4*x_20-0.2*x_30-2.4;
    x_21 = 0.25*x_10 -0.5*x_30+5;
    x_31 = -0.2*x_10+0.3*x_20+0.3;
    n = n+1;
    err1 = abs(x_11-x_10);
    err2 = abs(x_21-x_20);
    err3 = abs(x_31-x_30);
    err = max(err1, max(err2, err3));
    fprintf("n = %d,  ", n)
    fprintf("x_1 = %f,  x_2 = %f,  x_3 = %f,  ", x_11, x_21, x_31)
    fprintf("err = %f\n", err)
    x_10 = x_11;
    x_20 = x_21;
    x_30 = x_31;
end

运行结果1-Jacobi

n = 1, x_1 = -2.400000, x_2 = 5.000000, x_3 = 0.300000, err = 5.000000
n = 2, x_1 = -4.460000, x_2 = 4.250000, x_3 = 2.280000, err = 2.060000
n = 3, x_1 = -4.556000, x_2 = 2.745000, x_3 = 2.467000, err = 1.505000
n = 4, x_1 = -3.991400, x_2 = 2.627500, x_3 = 2.034700, err = 0.564600
n = 5, x_1 = -3.857940, x_2 = 2.984800, x_3 = 1.886530, err = 0.357300
n = 6, x_1 = -3.971226, x_2 = 3.092250, x_3 = 1.967028, err = 0.113286
n = 7, x_1 = -4.030306, x_2 = 3.023680, x_3 = 2.021920, err = 0.068570
n = 8, x_1 = -4.013856, x_2 = 2.981464, x_3 = 2.013165, err = 0.042216
n = 9, x_1 = -3.995218, x_2 = 2.989954, x_3 = 1.997210, err = 0.018637
n = 10, x_1 = -3.995423, x_2 = 3.002590, x_3 = 1.996030, err = 0.012637
n = 11, x_1 = -4.000242, x_2 = 3.003129, x_3 = 1.999862, err = 0.004819
n = 12, x_1 = -4.001224, x_2 = 3.000009, x_3 = 2.000987, err = 0.003121
n = 13, x_1 = -4.000201, x_2 = 2.999200, x_3 = 2.000247, err = 0.001023
n = 14, x_1 = -3.999730, x_2 = 2.999826, x_3 = 1.999800, err = 0.000626
n = 15, x_1 = -3.999890, x_2 = 3.000167, x_3 = 1.999894, err = 0.000341
n = 16, x_1 = -4.000046, x_2 = 3.000081, x_3 = 2.000028, err = 0.000155
n = 17, x_1 = -4.000038, x_2 = 2.999974, x_3 = 2.000033, err = 0.000106
n = 18, x_1 = -3.999996, x_2 = 2.999974, x_3 = 2.000000, err = 0.000041

经过18次迭代，误差满足条件
最终得到近似解：(-3.999996, 2.999974, 2.000000)

代码2-Seidel

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 简介：用Seidel迭代法求解线性方程组，要求误差小于10^(-4)
% 作者：不雨_亦潇潇
% 文件：Seidel.m
% 日期：20221102
% 博客：https://blog.csdn.net/weixin_43470383/article/details/127661516
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc; clear all;
x_10 = 0;
x_20 = 0;
x_30 = 0;
n = 0;
err = 1;

while err>10^(-4)
    x_11 = -0.4*x_20-0.2*x_30-2.4;
    x_21 = 0.25*x_11 -0.5*x_30+5;
    x_31 = -0.2*x_11+0.3*x_21+0.3;
    n = n+1;
    err1 = abs(x_11-x_10);
    err2 = abs(x_21-x_20);
    err3 = abs(x_31-x_30);
    err = max(err1, max(err2, err3));
    fprintf("n = %d,  ", n)
    fprintf("x_1 = %f,  x_2 = %f,  x_3 = %f,  ", x_11, x_21, x_31)
    fprintf("err = %f\n", err)
    x_10 = x_11;
    x_20 = x_21;
    x_30 = x_31;
end

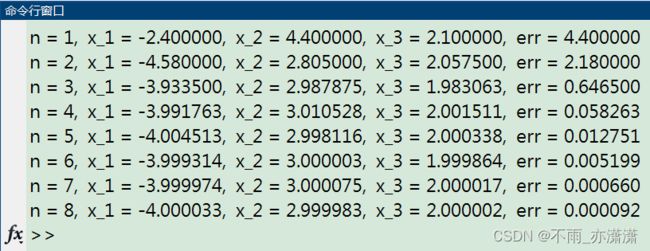
运行结果2-Seidel

n = 1, x_1 = -2.400000, x_2 = 4.400000, x_3 = 2.100000, err = 4.400000
n = 2, x_1 = -4.580000, x_2 = 2.805000, x_3 = 2.057500, err = 2.180000
n = 3, x_1 = -3.933500, x_2 = 2.987875, x_3 = 1.983063, err = 0.646500
n = 4, x_1 = -3.991763, x_2 = 3.010528, x_3 = 2.001511, err = 0.058263
n = 5, x_1 = -4.004513, x_2 = 2.998116, x_3 = 2.000338, err = 0.012751
n = 6, x_1 = -3.999314, x_2 = 3.000003, x_3 = 1.999864, err = 0.005199
n = 7, x_1 = -3.999974, x_2 = 3.000075, x_3 = 2.000017, err = 0.000660
n = 8, x_1 = -4.000033, x_2 = 2.999983, x_3 = 2.000002, err = 0.000092

经过8次迭代，误差满足条件
最终得到近似解：(-4.000033, 2.999983, 2.000002)

题目2-Sor迭代法

来源：《数值分析》第5版，清华大学出版社，作者：李庆扬等，第6章习题8

代码3-Sor

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 简介：用Sor迭代法求解线性方程组，要求误差小于10^(-4)
% 作者：不雨_亦潇潇
% 文件：Sor.m
% 日期：20221102
% 博客：https://blog.csdn.net/weixin_43470383/article/details/127661516
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc; clear all;
x_10 = 0;
x_20 = 0;
x_30 = 0;
n = 0;
err = 1;
omega = 0.9;

while err>10^(-4)
    x_11 = (1-omega)*x_10+omega*(-2.4-0.4*x_20-0.2*x_30);
    x_21 = (1-omega)*x_20+omega*(5+0.25*x_11-0.5*x_30);
    x_31 = (1-omega)*x_30+omega*(0.3-0.2*x_11+0.3*x_21);
    n = n+1;
    err1 = abs(x_11-x_10);
    err2 = abs(x_21-x_20);
    err3 = abs(x_31-x_30);
    err = max(err1, max(err2, err3));
    fprintf("n = %d,  ", n)
    fprintf("x_1 = %f,  x_2 = %f,  x_3 = %f,  ", x_11, x_21, x_31)
    fprintf("err = %f\n", err)
    x_10 = x_11;
    x_20 = x_21;
    x_30 = x_31;
end

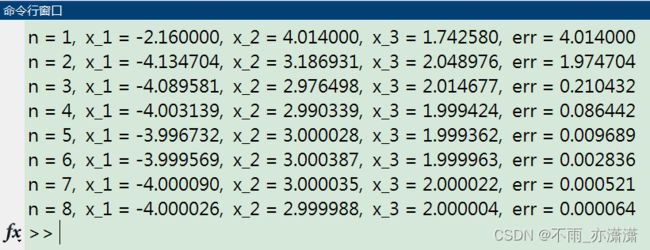
运行结果3-Sor

n = 1, x_1 = -2.160000, x_2 = 4.014000, x_3 = 1.742580, err = 4.014000
n = 2, x_1 = -4.134704, x_2 = 3.186931, x_3 = 2.048976, err = 1.974704
n = 3, x_1 = -4.089581, x_2 = 2.976498, x_3 = 2.014677, err = 0.210432
n = 4, x_1 = -4.003139, x_2 = 2.990339, x_3 = 1.999424, err = 0.086442
n = 5, x_1 = -3.996732, x_2 = 3.000028, x_3 = 1.999362, err = 0.009689
n = 6, x_1 = -3.999569, x_2 = 3.000387, x_3 = 1.999963, err = 0.002836
n = 7, x_1 = -4.000090, x_2 = 3.000035, x_3 = 2.000022, err = 0.000521
n = 8, x_1 = -4.000026, x_2 = 2.999988, x_3 = 2.000004, err = 0.000064

经过8次迭代，误差满足条件
最终得到近似解：(-4.000026, 2.999988, 2.000004)