ICDE2023 | VEND:基于点编码的边存在性判定
介绍
PKUMOD毕业生,湖南大学李友焕副教授论文《VEND:Vertex Encoding for Edge Nonexistence Determination》被ICDE 2023 接收。
这篇文章提出了一个在图数据领域至关重要的全新问题——通过给定的两个顶点去索引两点相连的对应边,这一边查询的基础操作在图数据库系统中随处可见,那么采用相应的策略去加速边查询操作将大幅度提升图数据库系统的查询效率以及吞吐量。
真实世界的图数据度数比点的个数要小的多,那么大多数点之间不存在相连的边。基于这一现象,本文提出了一种基于点编码过滤无边查询操作(vertex encoding for edge nonexistence determination ,VEND)的方法,避免访问图数据库磁盘,加速了边查询这一基础操作。与此同时,这篇文章还提出了对应的点编码更新算法以支撑图数据的更新。实验在多个大规模的真实图数据集中证明该方法能够检测出边查询中大部分的无边操作并有效的提升了查询性能。
一、背景知识
边查询不仅是图数据系统的基础操作之一,也在图计算中频繁执行。例如在知识图谱中根据给定的实体去搜索关系,聚集系数中通过查询两点之间是否存在边判断三角结构,子图匹配算法利用边查询扩展部分匹配结果。然而,并不是所有的边查询结果都会返回边,真实世界的图数据集中点的平均度数与点数相比相差甚远,所以对于一个顶点来说,与其相连的点数要远远小于不相连的点数,那么对于边查询来说大部分时间都被浪费在了无边查询上,过滤掉这些无边查询就可以提升图数据库的查询性能。
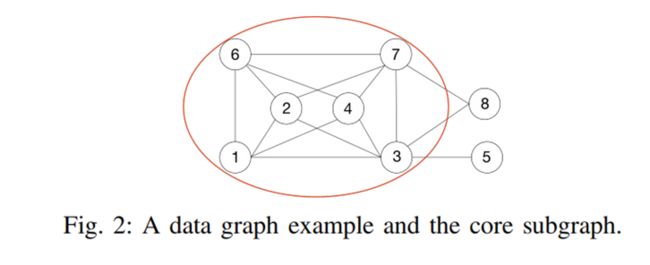
以vend加速基于磁盘的三角计数算法Trigon[1]为例。图数据以邻接表的形式组织并按照kv的方式存储在磁盘中,算法首先将磁盘中的数据按照顶点id顺序划分成若干个的分区,分区大小等同于内存大小。对于每一个分区P的顶点i,Trigon构建三元组
二、方法
为了兼顾时间与空间效率,本文将顶点的邻居序列编码成k维整数作为该点的编码,相较于顶点的平均度数,k往往很小,实验中k值分别取6,8,10。在边查询过程中,只需比较两个顶点的编码就能判断边是否存在。
1. 基于k-core的编码策略
为了在有限编码维度下使点的编码尽可能的包含大部分邻接点信息,本文首先采取了一种基于k-core[2]的编码策略。对于给定的无向图G和编码维度k,不断移除度数小于k的点直至剩余图中所有点度数不小于k,由于被移除的点度数小于k,可以直接将邻居id序列作为编码。显而易见,剩余图即为k-core图,本文分别提出了range、hash以及hybrid的方法对剩余点编码。
2. Range以及Hash Vend
这两种方法都是这篇文章的基准方法。
Range Vend: 对于1中获得的k-core图,每个顶点可以得到一个按照id增序排列的邻接点序列 。如果选取长度为k的子序列作为顶点v的编码,那么可以直接通过该编码判断顶点id在(min,max)范围内的点是否与顶点v存在边,这就是range vend的核心思想。显然易见,范围越大,包含的信息越多,那么编码能够过滤的无边就越多。此外,本文还提出了一点优化,将邻接点序列s扩展为s={-∞,v1,v2,…,v(n-1),vn,+∞},-∞和+∞,和分别代表所有顶点id的最小、最大值,选取最大范围子序列时也可以将其作为考虑。
Hash Vend: 基于范围的编码是显示的将邻居id进行编码,而对于判断边是否这一需求来说,可以通过hash的方法隐式编码。将所有邻居id按照hash的方式映射到k维对应的比特序列中,分别将对应的位置为1。在查询时,若对应的编码位为0则可说明不存在该邻居。
3. Hybrid Vend
Hybrid的编码方式结合了range以及hash的思想,在兼顾过滤效率的同时支持编码的快速更新,是本文的最优策略。
在hybrid编码方式中,一个顶点的编码包含range以及hash部分,range部分直接存储范围内的顶点id,hash部分将剩余邻居顶点id映射到剩余bit中,那么如何去取舍range的编码位数?本文提出了一种VEND score的指标来衡量编码过滤效果的优劣,VEND score有range范围大小以及hash后比特序列中0的个数共同计算,得分越高证明过滤效果越好。以VEND score为判断依据,hybrid Vend在不同range位数以及范围的情况下选取最优编码方案。
通过两个顶点编码即可判断两点之间是否存在相连边。在测试过程中优先判断直接编码的顶点,因为通过编码即可获取全部邻居信息。查询k-core图中点编码时,首先通过编码结构进行解码,例如hybrid vend前几位包含了range位数、顶点id位数等一系列信息。
对于数据图的插入删除操作,本文也提出了hybrid vend对应的编码更新策略,理论和实验都证明了编码更新能够在线性时间内完成。
三、实验
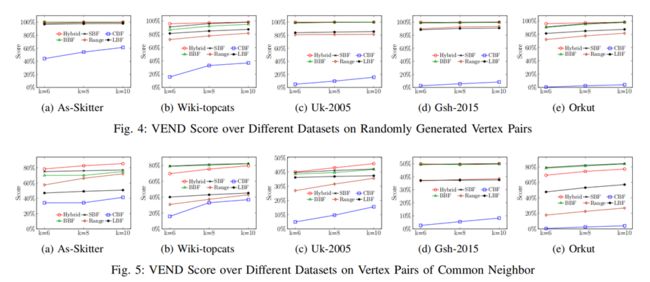
论文的实验部分在三种编码方式的基础之上添加了基于bloom filter编码的基准方案,在五个大规模真实图数据集中进行了验证。
其中各个编码方式vend score 得分以及边查询加速实现结果如下。
从vend score和边查询实验结果中可以看出本文提出的编码策略过滤了极高比例的边查询操作并显著的缩短了查询耗时,相较于基准方案有着明显的优势。
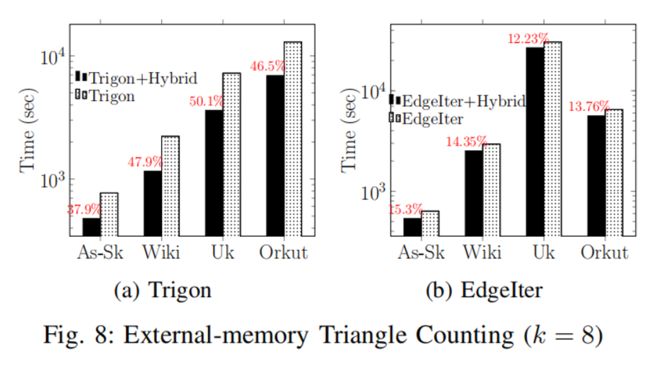
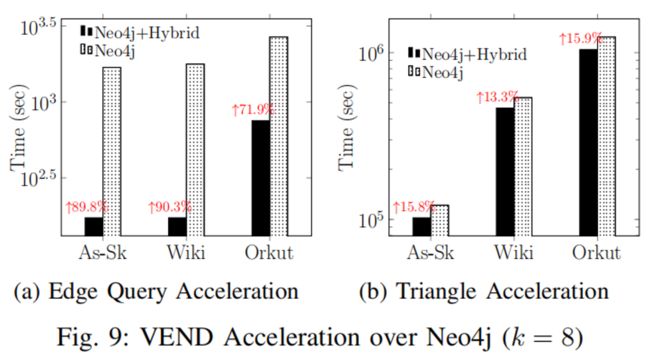
论文为了验证真实数据环境下Vend的有效性,分别进行了有关Trigon三角计数以及Neo4j[3]下查询加速效果的实验,实验结果如下。
从上图中可以看出在论文中的方法使Trigon算法提升了40%~50%的效率,在neo4j环境下提升了71.9%的边查询以及10%~15%的三角计数性能,验证了VEND在真实环境下的优势。
四、结论
这篇论文的贡献度可以分为以下几点:(1).提出了通过点编码方式判断边的存在性(VEND)这一全新问题,并设计了VEND score指标来衡量编码效果。(2).提出了高效的VEND编码策略,hybrid编码方式显著的提升了边查询效率并支持线性的编码更新。(3).大量的实验结果证明即使是基准的VEND策略也能明显提高查询系统性能并且hybrid策略在图数据环境下也保持着高效性。
参考文献
[1]. Cui, Yi, Di Xiao, Daren BH Cline, and Dmitri Loguinov. "Improving I/O complexity of triangle enumeration." IEEE Transactions on Knowledge and Data Engineering (2020).
[2]. Seidman, Stephen B. "Network structure and minimum degree." Social networks 5, no. 3 (1983): 269-287.
[3]. Miller, Justin J. "Graph database applications and concepts with Neo4j." In Proceedings of the southern association for information systems conference, Atlanta, GA, USA, vol. 2324, no. 36. 2013.
欢迎关注北京大学王选计算机研究所数据管理实验室微信公众号“图谱学苑“
实验室官网:https://mod.wict.pku.edu.cn/
微信社区群:请回复“社区”获取
实验室开源产品图数据库gStore:
gStore官网:http://www.gstore.cn/
GitHub:https://github.com/pkumod/gStore
Gitee:https://gitee.com/PKUMOD/gStore