人工智能基础 | 机器学习算法基础篇（三）

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RdD3JxKB-1667746138300)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/公众号横幅-1.png)]

前言

以下内容是在学习过程中的一些笔记，难免会有错误和纰漏的地方。如果造成任何困扰，很抱歉。

一、线性回归

回归，指研究一组随机变量 (Y1 ，Y2 ，…，Yi) 和另一组 (X1，X2，…，Xk) 变量之间关系的统计分析方法，回归分析是一种数学模型，当因变量和自变量为线性关系时，它是一种特殊的线性模型。

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DG8LKHQF-1667746138301)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/机器学习入门-线性回归模型公式-3.png)]

b为误差服从均值为0的正态分布，如果只有一个自变量的情况下就叫一元回归，如果有多个自变量的情况下就叫多元回归；

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qvAyUfR1-1667746138301)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/多元线性回归的简单公式-1.png)]

回归的目的是预测数组型的目标值

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-c7z9NgYB-1667746138302)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/乌鸦坐飞机.png)]

公式拆解

对于线性模型的定义公式为：f(x) = w0 + w1·x1 + w2·x2 + … + wn·xn

当通过矩阵表示时：f(x) = XW，W是根据要求得到的非输入式参数，X是输入的数据矩阵

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GO2zqddF-1667746138302)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/线性模型-W的矩阵-1.png)]

n代表一个数据有n个数据，m代表一共是m个数据

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oS7SECeH-1667746138302)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/线性模型-X的矩阵-1.png)]

那么数据集的数据矩阵为

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZuA6W12v-1667746138303)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/线性模型-Y的矩阵-1.png)]

线性回归模型的最终目标就是找到参数 W 来使得 f(x) = XW 尽可能无限贴近 Y

代码实践

不引用深度学习框架，通过简单的数学公式完成一元回归案例

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

np.random.seed(0)
area = 2.5 * np.random.randn(100) + 25
price = 25 * area + 5 + np.random.randint(20, 50, size=len(area))

data = np.array([area, price])
data = pd.DataFrame(data=data.T, columns=['area', 'price'])

# 绘图
# plt.scatter(data['area'], data['price'])
# plt.show()

W = sum(price * (area - np.mean(area))) / sum((area - np.mean(area)) ** 2)
b = np.mean(price) - W * np.mean(area)
# print("计算回归系数", W, b)

y_pred = W * area + b

# 绘图
plt.plot(area, y_pred, color='red', label="forecast")
plt.scatter(data['area'], data['price'], label="train")
plt.xlabel("areaX")
plt.ylabel("priceY")
plt.legend()
plt.show()

绘图输出

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tlKE0zYt-1667746138303)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/连续值预测-一元线性简单效果图-1.png)]

对数几率回归

Logistic Regression，属于机器学习中的入门的分类器，在此前的案例模型对连续值进行预测分析，输出的也是连续值，但是如果是分类任务则没有办法采用以往的解决方案，通过广义线性回归，解决了线性回归不擅长的分类问题，常用于二分类。

如果在线性模型的基础上做二分类任务，实际上就是在最终的输出结果上套上一层函数，最简单的就是“单位阶跃函数”(unit-step function)，通过结果输入进行逻辑分类

换个角度思考，实际上就是在线性回归模型的加入最后一个感知器层，我们通过逻辑回归与交叉熵，对分类问题进行实际演示，首先查看数据集

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-awCVQ7vg-1667746138303)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/tensorflow-逻辑回归与交叉熵的数据集简图-1.png)]

通过前面的数据，得出最后的数据是1还是-1，然后看看代码

import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 加载数据 header=None 意思是没有列头
data = pd.read_csv(
    'E:/27_Python_Protect/02_ml/01-识别手写数字/credit-a.csv', header=None
)

# print(data.head())

# 取值 特征数据 目标数据
x = data.iloc[:, :-1]
y = data.iloc[:, -1:].replace(-1, 0)

# 导入Sequential模型
model = tf.keras.Sequential(
    [
        tf.keras.layers.Dense(4, input_shape=(15,), activation='relu'),
        tf.keras.layers.Dense(4, activation='relu'),
        tf.keras.layers.Dense(1, activation='sigmoid')
    ]
)

# 模型的优化方法 损失函数选择 === metrics 计算正确率 评估指标算子
model.compile(
    optimizer='adam',
    loss='binary_crossentropy',
    metrics=['acc']
)

history = model.fit(x, y, epochs=10000)

# 预测代码忽略...

损失函数

对于任何机器学习问题，都需要先明确损失函数，在遇到回归问题时，通常我们会直接想到如下的损失函数形式

• 均方误差（Mean Square Error，MSE）
• 平均绝对误差（Mean Absolute Error，MAE）
• 均方根误差（Root Mean Square Error，RMSE）
• 均方对数误差（Mean Squared Log Error）
• 平均相对误差（Mean Relative Error，MAE）

1

二、决策树

决策树是一种常见的机器学习方法，常用于分类问题，顾名思义，决策树是基于树结构来进行决策的，例如下面这颗在西瓜书中的一颗非常有辨识度的决策树

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZGAJbzwi-1667746138303)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/西瓜决策树-1.png)]

很像在代码中if-else里疯狂嵌套，决策过程中的最终结论对应了我们所希望的判定结果，其体现的是一种“分而治之”的策略，目的是为了产生一颗泛化能力强、处理未知属性能力强的一颗决策树。

信息熵与信息增益

1

决策树的组成与建立

1

决策节点

叶子节点

决策树深度

划分标准

1

三、支持向量机

支持向量机（Support Vector Machine），SVM

1

四、贝叶斯分类

1

五、K-近邻算法

k-近邻（k-Nearest Neighbor），KNN

定义

k-近邻（k-Nearest Neighbor，简称KNN）学习是一种常用的监督学习方法，其工作机制非常简单：给定测试样本，基于某种距离度量找出训练集中与其最靠近的k 个训练样本，然后基于这k个“邻居”的信息来进行预测。————根据你的“邻居”判定你的类别，你周围的人决定了你是怎样的人

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QtW8CAeS-1667746138304)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/两个样本之间的欧氏距离图片-1.png)]

两个样本之间的距离通过欧氏距离公式计算，公式如下

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wDSz644Z-1667746138304)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/欧式距离公式-1.png)]

跟之前的学习方法相比，k-近邻是没有明显的训练过程，它是“懒惰学习”的代表，训练阶段仅仅是将样本保存，待收到测试样本后再进行处理，相对应的其它学习处理的方法，叫“急切学习”。

通过案例认识k-近邻

如何通过KNN推算出唐人街探案的电影类型？

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JeeITBnP-1667746138304)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/K近邻的简单示例-1.png)]

通过KNN的算法思想，最后得到每个电影和被预测的电影的距离

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9RqZiEOd-1667746138304)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/K近邻的简单示例-计算解析-1.png)]

结果如下

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-enNiga12-1667746138305)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/K近邻的简单示例-计算解析-2.png)]

但是最终，我们不能通过单一的最近的距离结果，得到我们想要的答案，因为会可能存在的问题是，9个人觉得我帅，1个人觉得我丑，这1个人距离我最近，难道我就要听他的吗？他就是对的吗？所以一般情况下我们会根据结果的倒叙的第一、第三、第五的结果进行判别。

使用sk-learn实现k-近邻案例

实现API：n_neighbors，int类型，可选参数，默认值为5，功能为查询默认使用的邻居数

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)

完整代码

from sklearn.neighbors import KNeighborsClassifier

# x特征为多维数组
x = [[1], [2], [0], [0], ]
y = [1, 1, 0, 0]

# 导入算法模型
estimator = KNeighborsClassifier(n_neighbors=2)

# 数据训练
his = estimator.fit(x, y)

# 进行预测 入参依旧是多维数组
ret = estimator.predict([[3]])
print(ret)

总结

1. 计算已知类别数据集中的点与当前点的距离
2. 按距离递增次序排序
3. 选取与当前的点距离最小的k个点
4. 统计前k个点所在的类别的出现频率
5. 返回前k个点出现频率最高的类别作为当前预测点的分类类别

距离度量

地址
Python随记系列 —— 目录_繁依Fanyi的CSDN博客

• 欧式距离
• 曼哈顿距离/城市街区距离
• 切比雪夫距离
• 闵可夫斯基距离

曼哈顿距离

又名城市街区距离，由于有阻挡物，无法通过欧式距离进行两点间的最短距离，故而产生该距离算法得到最短街区距离

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-91gagsfq-1667746138305)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/曼哈顿距离图-2.png)]

公式如下

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xHo3ihCR-1667746138305)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/曼哈顿距离公示图-1.png)]

切比雪夫距离

国际象棋的棋盘上，一场大战正在进行，“车”横冲直撞，干掉敌人；“皇后”肆意横行，大开杀戒；而国王，只能在自己周围的 “横”、“竖”、“斜” 几个方块里移动

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RSHENwdJ-1667746138305)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/切比雪夫距离棋盘图-1.png)]

切比雪夫距离 (Chebyshev Distance) 研究的就是关于 “国王” 移动的问题，国王从一个格子 (x1,y1) 走到 另一个格子 (x2,y2) 最少需要的步数就是 切比雪夫距离 ，数学公式为

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-07HvCKji-1667746138306)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/切比雪夫距离公式-1.png)]

闵可夫斯基距离

闵氏距离并不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性的表述，将多个距离公式总结成为的一个公式

假设两个n维的变量

• A( x11,x12,…,x1n )
• B( x21,x22,…,x2n )

通过两个n维变量组成闵氏距离公式为

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UCzq4kVK-1667746138306)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/闵氏距离公式-1.png)]

咋一看，跟前面所述的“将多个距离公式总结成为的一个公式”一话并不是很相符，但是实际上，通过P值的变化，结果公式也将不同

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-p3dOL1Lv-1667746138306)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/闵氏距离公式-分类图-1.png)]

根据P的不同，闵氏距离可以某一种的距离，它的优点在于同时能够多种距离度量，但是同时也暴露其缺点

• 没有考虑各个分量的分布（期望，方差等）可能是不同
• 单位相同看待

例如：身高相差10对比体重相差10的概念是不一样的

标准化欧氏距离

解决闵氏距离的一种改进，要针对变量 x 进行了修改，使其变成了标准化变量，数据各维分量的分布不一样，那就先将各个分量都标准化到均值、方差等；

假设样本集 X 的均值 (mean) 为 m ，标准差 (standard deviation) 为 s ，那么 X 的标准化变量为

带入公式后可得

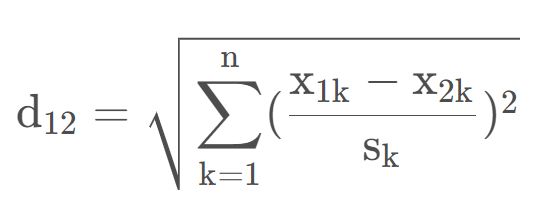
从公式看还是蛮复杂的，我们引入实际案例来看

数据集 X = [  [ 1 , 1 ] ,  [ 2 , 2 ] ,  [ 3 , 3 ] ,  [ 4 , 4 ]  ]
假设两个变量的标准差为 0.5 和 1 （多维数组，最小维度索引0为x，最小维度索引1为y）

经过计算后的结果是
d = 2.2361   4.4721   6.7082   2.2361 ........

余弦距离

几何中，夹角余弦可用来衡量两个向量方向的差异；在机器学习中，用来衡量样本向量之间的差异

汉明距离

两个等长的字符串s1和s2的汉明距离：将一个字符串变成另一个字符串所需要的替换次数

杰卡德距离

用来衡量两个集合差异性的一种指标，两个集合A和B的交际元素在A，在B的并集里所占的比例，称为两个集合的杰卡德相似系数，通过符号表示为

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-asvc5QSZ-1667746138306)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/杰卡德距离公式简单图-1.png)]

马氏距离

是基于样本分布的一种距离，同时也表示数据的协方差距离，它是一种有效的计算两个位置样本集的相似度的方法

k值（邻居数）的选择

如果k过小：容易受到异常点的影响，k值的减小意味着整体模型将变得复杂，过拟合；

如果k过大：遭受样本均衡问题，k值的增大意味着整体模型变得简单，欠拟合；

这里涉及到统计方法论，需要通过合适的误差（近似误差、估计误差）进行判断，具体情况具体分析。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3ZTuYYbG-1667746138307)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/魔方块图片-1.png)]

KD树

实现KNN算法时，如何对训练数据进行快速KNN搜素，在最简单的情况下，就是通过遍历穷举的方式，计算输入的实例对每个训练的实例的距离，计算存储后，再去查找KNN，简单但是效率比较低且耗时。

KD树的存在就是为了解决上述问题，为了避免每次重新计算距离，算法会把距离信息保存在一棵树里，每次计算之前先查询距离信息，避免重新计算下产生的耗时，

六、梯度下降

1

七、集成学习

1

八、聚类算法

1

九、西瓜树看看补充

1

1

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4Jnbx3i3-1667746138307)(https://csdn-pic-1301850093.cos.ap-guangzhou.myqcloud.com/csdn-pic/小星球-1.png)]