吴恩达教授机器学习课程笔记【七】- Part 7 最优模型选择

本节为吴恩达教授机器学习课程笔记第七部分，最优模型选择，主要包括：模型选择方法、特征选择方法以及贝叶斯统计的部分知识。具体地，有留存法交叉验证和k-折交叉验证、启发式地前向和后向特征搜索策略、过滤器特征选择策略以及贝叶斯最大后验估计。

  假设我们现在有一个有限的模型集$M=\{M_1,...,M_d\}$，要从中选择一个模型，比如$M_i$是一个$i$阶的多项式回归模型，或者我们要从支持向量机、神经网络或者逻辑回归中选择一个模型，该如何选择？

1. 交叉验证

  给定一个训练集$S$，假如使用经验风险最小化的方式来寻找一个最佳模型，即第一步在训练集上逐个训练$M_i$，得到假设函数$h_i$，第二步从中选择一个训练误差最小的假设函数。
  但是这样的算法并没有什么效果。比如我们要从一个多阶的多项式假设类中选择一个模型，那么多项式阶数越高，训练误差必然越低，也就是说，经验风险最小化的方法总会选择一个高方差高阶的多项式模型，这种选择通常泛化效果并不好。
  有一个更好地选择，即留出法交叉验证，也叫简单交叉验证，第一步：随机将训练集划分为训练集$S_{train}$(70%)和留存交叉验证集$S_{cv}$；第二步在训练集$S_{train}$上训练模型$M_i$，得到假设函数$h_i$；第三步选择留存交叉验证集上经验误差${\hat{\epsilon }}_{S_{cv}}(h_i)$最小的假设函数$h_i$。
  通过在不参与训练的留存集上进行模型测试，我们可以对每一个假设函数$h_i$的泛化误差有一个更好的估计然后选择泛化误差最小的一个。通常这个留存集比例占1/4~1/3之间即可，典型的比例即30%。
  有时候留存交叉验证的第三步也可以改为：选择在留存集上具有最小经验风险的模型之后，在$S$上重新训练模型。但是这种方法对于那些对初始条件/数据的扰动比较敏感的模型并不适用，因为在训练集上表现好的模型在留存验证集上不一定表现好。
  使用留出法交叉验证的确定在于它浪费了30%的数据，即便我们重新在整个训练集上训练模型，我们选择的模型也是在0.7m的训练集上训练的，如果数据本身比较廉价易得，这种方法就阔以，但是如果数据稀缺，那么可以使用另一种交叉验证方法，即k折交叉验证，每次仅保留较少的数据，第一步随机将$S$分为$k$个不相交的子集，每个子集有$m/k$个训练样本；第二步，对于每个模型按如下步骤进行评估：进行$k$轮循环，每个循环都在除$S_j$之外的所有子集的并集上训练每个模型$M_i$得到假设函数$h_{ij}$，然后在$S_j$上测试假设函数，得到经验风险${\hat{\epsilon }}_{S_j}(h_{ij})$，模型$M_i$的经验风险最后取所有的平均；第三步，选择泛化误差最小的一个模型。然后在整个数据集上重新训练模型，得到的假设函数就是k-折交叉验证法的输出。
  通常取$k=10$，每次留存的数据更小，整个算法的计算代价也就更高。
  尽管$k=10$是一个常用的选择，但是在数据非常少的情况下，我们也可以令$k=m$即每次训练尽可能留存最少的样本数(每次保留一个样本不参与训练)，这种方法又被称为留一法交叉验证。

2. 特征选取

  讨论完模型选取，下面看特征选取。考虑一个特征数量巨大的有监督学习任务，假设特征数量$n>>m$，但是其中仅仅有为数不多的特征与学习任务相关。如果对$n$个输入特征应用简单的线性分类器，假设函数的VC维也会达到$O(n)$的复杂度，这时候，除非训练集样本数量相当大，否则就可能出现过拟合。
  这时候就需要使用特征选择算法来减少特征数量了。给定$n$个特征，则存在$2^n$个特征的组合，这时候的特征选择可以视为一个对$2^n$个模型进行模型选择的问题。然而对于较大的$n$，这样的计算代价过于高昂，所以一些启发式搜索的方法就被用到了这里，下面的搜索方法称为前向搜索：

  算法内层循环，遍历所有不在$F$中的特征，选择一个泛化误差最小的特征加入$F$；外层循环则不断重复这个过程，直到$F$已经包含了全部的特征或者$F$中特征数量已经达到我们设定的上限，这种算法也称为包装器特征选择，还包括后向搜索，即初始$F$包含所有的特征，然后每次减少一个，但是这种方法相比于前向搜索的计算代价有过之而无不及，并且二者都属于贪心算法，容易陷入局部最优解。同时若特征间存在相互依赖的关系前向搜索可能造成特征的重复。
  过滤器特征选择方法则给出了一种同样启发式但是计算代价更低的算法。方法的思想是构建一个特征与最终输出标签的关联分数评估公式，这样我们就可以挑选$k$个分数最大的特征。
  一种可行的公式构建方法即衡量$x_i$和$y$的相关性，从而选择与输出标签相关性最大的特征。但是实践中，特别是对于离散的特征，我们更多会选择$x_i$与$y$的互信息作为分数评价公式：

  互信息也可以写为KL散度的形式：

  KL散度描述的是$p(x_i,y)$和$p(x_i)p(y)$不同的概率，如果$x_i$和$y$互相独立，那么上面两个式子就相等，也就是说分数为0。确定了特征的分数之后，如何确定选择前k个特征的k，这时候可以应用交叉验证的方式，来从一组k中选择一个最合适的k。比如，在文本分类中应用朴素贝叶斯时，字典的规模通常很大， 这时候就可以使用特征选择方法选择一个更好的特征子集。

3. 贝叶斯统计与正则化

  该部分讨论另外一个避免过拟合的方法，我们之前使用极大似然方法进行参数拟合时，按照如下的公式选择参数：

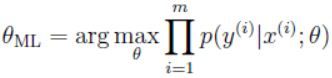
  在之后的讨论中，我们将$\theta$视为未知常量。(频率主义学派的观点$\theta$并不是随机的，只是恰好未知，我们的任务就是通过统计学方法来找到参数的最佳估计)。
  另一种可选的参数估计方法就是以贝叶斯学派的角度来看问题并且把$\theta$视为未知的随机变量，这里我们用一个先验分布$p(\theta )$表示对于参数的已知情况的描述。给定训练集$S=\{(x^{(i)},y^{(i)}){\}}_{i=1}^m$，当我们需要对一个新的$x$值进行预测时，我们需要计算参数的后验分布：

  上述公式中，$p(y^{(i)}|x^{(i)},\theta )$和你选择的学习算法有关，比如使用贝叶斯逻辑回归，那么：

  其中：

  当我们测试新的样本$x$时，就可以使用参数的后验估计来进行预测：

  因此，如果目标是给定$x$输出$y$，那么我们可以输出：

  这个过程可以认为是做完全贝叶斯预测，因为我们的预测是对后验分布取均值，然而这个后验分布的计算通常非常困难，因为它需要求$\theta$的积分，而参数通常维度很高，并且不能以闭合形式完成。
  所以实践中，我们通常对后验分布取近似，常用的近似方法是使用单点估计，对$\theta$的最大后验估计由下式给出：

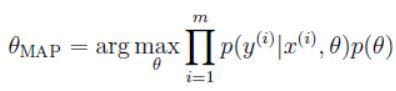
  除了先验概率分布，和极大似然估计相似。
  在实际应用中，我们通常假设先验概率分布服从分布：

  使用这个先验分布，拟合的参数${\theta }_{MAP}$通常比极大似然估计的要更小，这也使得贝叶斯最大后验估计在实际中更容易比极大似然估计能够避免过拟合。比如说贝叶斯逻辑回归在文本分类领域是一个很好的算法，即使文本分类中，通常用$n>>m$。

---

欢迎扫描二维码关注微信公众号 深度学习与数学   [每天获取免费的大数据、AI等相关的学习资源、经典和最新的深度学习相关的论文研读，算法和其他互联网技能的学习，概率论、线性代数等高等数学知识的回顾]