数据结构——双向循环链表
文章目录
- ⭐带头双向循环链表
-
- ✨带头双向循环链表结构定义
- ✨基本函数接口
-
- 双向链表初始化
- 双向链表尾插
- 双向链表尾删
- 双向链表头插
- 双向链表头删
- 中间结点——某结点前方插入(带结点查找函数Find)
- 擦除函数
- 修改函数
- 双向循环链表销毁
- ⭐后话
⭐带头双向循环链表
单链表在存储数值和数值的增删查改上有诸多不便,其在搜索遍历和结点查询上对数据的访问实质上并没有比顺序表的时间复杂度有更多的优势,诸如尾插尾删必须要遍历链表上,单链表的优势并不明显。但有一种便于数据访问和存储的优化链表,其弥补了单链表和顺序表上的种种不足,以更低的时间复杂度和更优的结构用来存储数据,方便用户增删查改。
✨带头双向循环链表结构定义
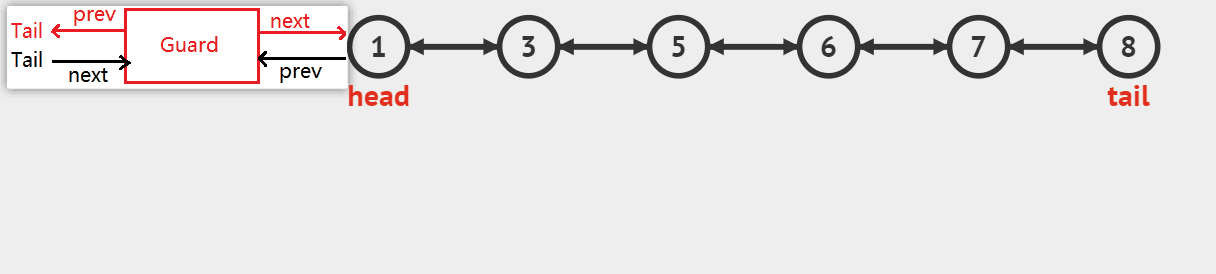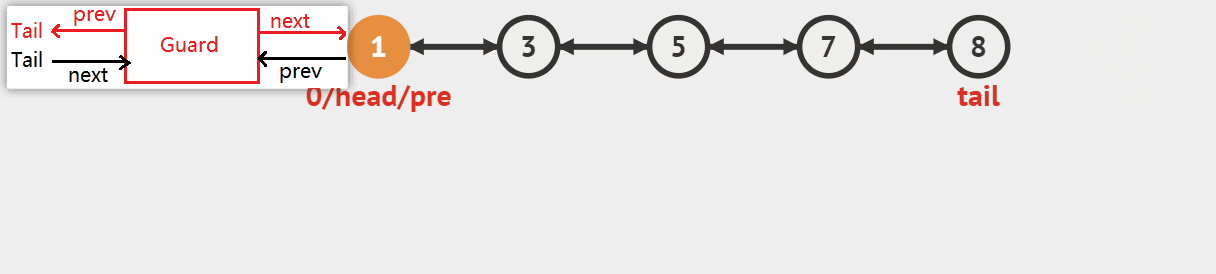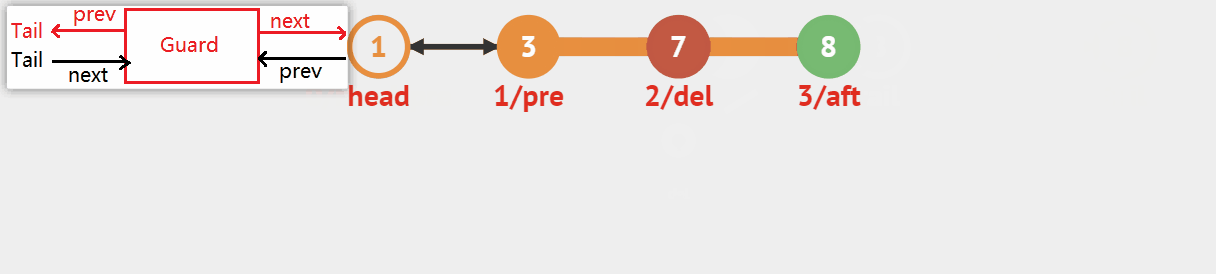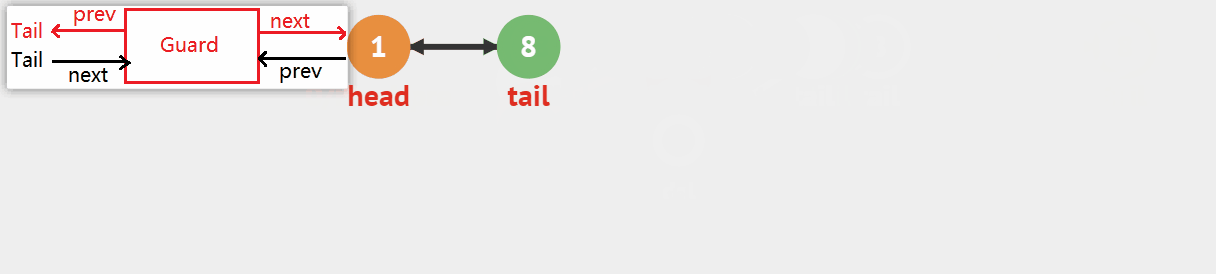
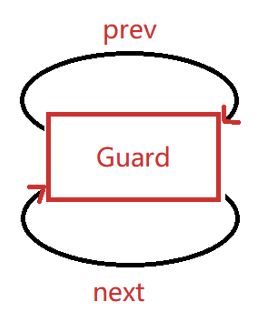
双向循环链表,在原单链表的基础上多了一个指向上一个结点的前驱指针prev,这样前后结点就不仅仅有了单向的从头至尾的指向顺序,也可以从后指向前,从末结点指向头结点。
原理图如下:

双向带头循环链表结构
typedef int DGREtype;
typedef struct DoubleGuardRoundList
{
DGREtype data;
struct DoubleGuardRoundList* next;
struct DoubleGuardRoundList* prev;
}DGR;
加入前驱指针后,不管是对于链表数据的尾插尾删,或是头插头删,其时间复杂度都为O(1),大大简化了链表遍历过程,而可以直接在链表首尾增减数据,因为一个链表的末节点可由头结点的前驱指针直接访问而不需要遍历至尾。
为了简化文本描述,本章双向循环带头链表均简称为双向链表。
✨基本函数接口
双向链表初始化
单链表不需要进行初始化操作,因为结点都是即时开辟即时使用,而带头双向循环链表为了考虑循环和其他插入操作的便利性,引入了头哨兵结点,开辟该结点作为循环链表的头结点,其不存储实际有效数值,并包含指向其本身的前驱和后继指针,用于在之后插入数值时改变指向,图如下所示:
双向链表初始化函数
DGR* DGRInit()
{
DGR* GuardNode = (DGR*)malloc(sizeof(DGR)); //动态申请开辟头哨兵结点
assert(GuardNode);
GuardNode->next = GuardNode; //让头结点前驱和后继指针指向其自身
GuardNode->prev = GuardNode;
GuardNode->data = NULL; //数值域置0,不代表有效数据
return GuardNode; //将该结点返回给实参头指针
}
- 与在单链表中的操作基本相同的是,每次动态申请和开辟结点空间都必须用户向系统显性地申请,因而同样可以将开辟结点的函数封装起来,便于后续链表结点的开辟使用和链接。
双向链表结点开辟函数
DGR* BuyListNode(DGREtype x) //将需要存储的值作为参数传入
{
DGR* NewNode = (DGR*)malloc(sizeof(DGR)); //动态开辟结点结构体空间
assert(NewNode);
NewNode->data = x; //结点数值域赋值,并将结点前驱和后继指针置空
NewNode->next = NULL;
NewNode->prev = NULL;
return NewNode; //返回该结点
}
- 结点申请函数中仅传入需要存储的数值x,动态开辟并断言内存空间的有效性后,将数值域赋值并将一个双向循环结点的前驱和后继指针都置空,这样做是为了方便后继其他函数引用该结点时能正确精准地将其指向有意义的其他结点地址,使其与链表链接起来。
- 带头双向循环链表由上图可以看出,其末结点的后继直接指向了头结点,因而于链表中不存在指向空的末结点,如果以该标准作为该链表的遍历循环结束条件则必定会死循环。为了方便观察循环链表,对链表进行遍历时的循环条件应改为使遍历指针当指向头结点时则结束循环。
双向链表遍历函数
void DGRPrint(DGR* Guard) //传入双向循环链表头哨兵地址
{
assert(Guard); //检查头地址有效性,如果哨兵结点不存在则没有链表可供遍历
DGR* cur = Guard->next; //从哨兵结点后继的真正首结点开始遍历打印
printf("Guard->");
while (cur != Guard) //循环结束条件为当遍历指针不为哨兵地址时,继续遍历
{
printf("%d->", cur->data); //打印结点值
cur = cur->next;
}
printf("Guard\n");
}
- 双向链表初始化完成后仅有哨兵位一个无实际意义的结点,为了方便观察,在遍历打印的数值前后加上代表哨兵结点位置的Guard,可以表示链表从头结点的后一个结点开始遍历,并最终循环回到头哨兵结点而结束遍历:
DGR* Guard = DGRInit();
DGRPrint(Guard);
空链表遍历结果如下:
Guard->Guard
双向链表尾插
双向循环链表尾插对比单链表最大的好处在于,对于一个仅有头哨兵结点的空链表或已存储有效数值的非空链表,末节点的搜索访问不再需要通过遍历链表至末尾,而只需通过头结点的前驱结点就可以直接找到,进而直接将带数值的新结点尾插到链表中,改变前后指向即可完成尾插操作,整个过程时间复杂度为O(1),与顺序表尾插效率一致。
原理图如下:
- 图中head为双向链表真正的首结点,其实际存储有效数值并由哨兵结点的后继next所指向,head的前驱也直接指向哨兵结点Guard。而哨兵结点Guard作为头结点存在只是为了让链表更加方便地进行插入和删除操作,因为可以不需要考虑头结点指针变更而需要传入二级指针或带返回值的问题,只不过在链表完全销毁时需要额外对哨兵结点进行释放,总体而言让链表的其他函数操作变得更加容易了。
- 每次尾插时,为了将新开辟的带值结点放到链表的末尾,通过访问哨兵头结点的前驱结点,即原链表的末结点,让末结点的后继直接指向新结点,并改变新结点的后继指向哨兵结点,而前驱指针指向原末结点,最后再改变哨兵结点的前驱指针由原末节点变更指向新末结点即可
双向链表尾插函数
void DGRPushBack(DGR* Guard, DGREtype x) //将哨兵结点和待存储值传入
{
assert(Guard);
DGR* NewNode = BuyListNode(x); //开辟待存储值的新结点
NewNode->next = Guard; //改变新结点前后指向,前指原末结点,后指哨兵结点
NewNode->prev = Guard->prev;
Guard->prev->next = NewNode; //改变原末结点的后继指向新结点
Guard->prev = NewNode; //改变哨兵结点的前驱指向新结点,完成链接
}
-
值得注意的是,原末节点只能通过哨兵结点的前驱指针进行访问Guard->prev,且对于新结点前驱指针链接原末节点的操作必须在新结点链接入链表步骤之前完成,因为一旦新结点插入时将哨兵结点的前驱直接指向新结点,则会出现原末节点丢失访问的情况,从而必须从头遍历至末尾才能找到了,所以新结点和其相邻的原末结点及哨兵结点的指向改变顺序很重要,可以总结如下:
第一,因为新结点NewNode自结点开辟函数BuyListNode出来后,其前驱和后继都是置空态,仅有数值域被赋值。直接改变其后继指向哨兵结点Guard,前驱指向原末结点Guard->prev(此时哨兵前驱还是原来的末节点地址)。
第二,改变原末节点的后继指向新结点Guard->prev-> next = NewNode,如果不进行此步骤,原末节点的后继仍继续指向哨兵结点,从而遍历时会直接将新的尾插结点跳过,造成尾插失效但数值占用内存的情况。
第三,最后才能改变哨兵结点的前驱指向,此时新的尾插结点已经在链表中变为新末结点,且除了哨兵前驱指针,其余指针都正确完成了指向的改变,直接改变哨兵结点的前驱指针Guard->prev = NewNode为新结点地址,即完成整个尾插新结点的插入和链表的整体循环。
-
除了此种方法外,还可以采用定义DGR* Tail指针临时指向原末节点将其地址备份的方法,则可以无需考虑指向改变的前后顺序问题,因为地址不会丢失,直接依次完成地址和前驱后继指针的指向改变即可。
测试用例
//在已初始化完成的空双向循环链表下加入如下语句
DGRPushBack(Guard, 1);
DGRPushBack(Guard, 2);
DGRPushBack(Guard, 3);
DGRPushBack(Guard, 4);
DGRPushBack(Guard, 5);
//打印链表
DGRPrint(Guard);
观察结果
Guard->1->2->3->4->5->Guard
观察调试

双向链表尾删
因为可以通过哨兵结点直接访问末节点地址,所以也不需要如同单链表那般从头遍历至尾再进行末节点的删除,而只需通过哨兵Guard的前驱prev进行直接地址访问,改变指向并释放结点空间即可。
原理图如下:
- 如果双向链表为空,则直接返回函数而不进行任何删除操作。如果不为空,即存在存储有效数值的首结点head或其他结点,则先将链表中倒数第二个结点Guard->prev->prev改为由哨兵结点的前驱指针直接指向,此时倒数第二个结点的后继指针仍指向末结点,将其释放后,倒数第二个结点成为了新链表的新末结点,再改其后继直接指向哨兵结点即可。
双向链表尾删
void DGRPopBack(DGR* Guard)
{
assert(Guard);
if (Guard->next == Guard) //如果链表为空,不进行任何操作
{
return;
}
else //如果非空,按序执行如下操作
{
Guard->prev = Guard->prev->prev; //哨兵前驱指向倒数第二个结点
free(Guard->prev->next); //释放原末结点
Guard->prev->next = Guard; //新末节点后继指向哨兵结点
}
}
- 如果链表中仅存在一个结点,即首结点head,则此时倒数第二个结点即为哨兵结点,根据上述步骤,将原先哨兵前驱指针指向的首结点指向其自身,释放首结点后再将哨兵结点后继指向其自身,同样可以完成首结点的尾删和哨兵结点的自指向,不会因为存储有效数据的首结点丢失而需要改变头结点地址,这也体现了哨兵结点的一大好处。
测试用例
//对于存在1,2,3,4,5五个数据的双向链表尾删3次
DGRPopBack(Guard);
DGRPopBack(Guard);
DGRPopBack(Guard);
DGRPrint(Guard);
//此时仅剩两个有效数据,再次进行3次尾删
DGRPopBack(Guard);
DGRPopBack(Guard);
DGRPopBack(Guard);
Guard->1->2->Guard
观察结果
Guard->1->2->Guard
Guard->Guard
由此可见,尾删后若存在数据,链表可以正常链接前后指针并打印;如果将链表删除干净并额外多删,也不会影响哨兵头结点的删除,此时链表为空。
双向链表头插
头插对于顺序表而言需要将其后面的数据整体后挪,而单链表或双向链表仅需改变指向即可,时间复杂度为O(1)。
原理图如下:
- 对于没有引用哨兵结点的单链表,其头插操作需要不断改变头结点地址Head并需要返回新链表头结点地址或使用二级指针的方式,虽然操作简单且时间复杂度也为O(1)。而对于引用了哨兵伪头结点的双向链表而言,每头插一个新开辟的带数值结点,就需要改变哨兵结点的后继指向Guard->next,虽然代码功能定义比单链表相比较为复杂一些,但整体还是较简洁且完整的。
双向链表头插函数
void DGRPushFront(DGR* Guard, DGREtype x)
{
assert(Guard);
DGR* NewNode = BuyListNode(x); //1. 开辟新带值结点
NewNode->next = Guard->next; //2. 改变新结点的前后继指向
NewNode->prev = Guard;
Guard->next = NewNode; //3. 链接哨兵结点后继指向为新结点地址
NewNode->next->prev = NewNode; //4. 改变原首结点的前驱指向为新结点地址
}
- 先将原双向链表存储有效数值的首结点地址Guard->next由新结点后继指针直接指向,而新结点的前驱指针也直接指向哨兵结点Guard。修改哨兵结点的后继指向新结点地址,并同时修改原首结点的前驱指向新结点,因此便完成了新结点的链接和首结点的插入。
- 要注意原首结点的地址Guard->next需要备份在新结点链接之前,如果一开始就直接将哨兵结点后继直接指向新结点,则原首结点及之后的所有结点地址均会丢失,造成该链表遍历只有新的首结点和其后指向的NULL值。
测试用例
//对于已经存在结点的原链表1,2,3,4,5进行头插
DGRPushFront(Guard, 0);
DGRPushFront(Guard, -1);
DGRPushFront(Guard, -2);
DGRPushFront(Guard, -3);
DGRPrint(Guard);
//对仅有哨兵结点的空链表进行头插
DGR* Guard = DGRInit();
DGRPushFront(Guard, 0);
DGRPushFront(Guard, 1);
DGRPushFront(Guard, 2);
DGRPushFront(Guard, 3);
DGRPrint(Guard);
观察结果
Guard->-3->-2->-1->0->1->2->3->4->5->Guard
Guard->3->2->1->0->Guard
首结点地址head一直在更改,而哨兵头结点地址保持不变。
双向链表头删
头删与头插如出一辙,原理图如下:
双向链表头删函数
void DGRPopFront(DGR* Guard)
{
assert(Guard);
if (Guard->next == Guard) //1. 如果链表为空,不执行头删
{
return;
}
else
{
Guard->next = Guard->next->next; //2. 链表第二个结点由哨兵后继直接指向
free(Guard->next->prev); //3. 释放首结点
Guard->next->prev = Guard; //4. 第二个结点成为新的首结点,改变前驱指向为哨兵结点
}
}
测试用例
//将1,2,3,4,5的双向链表进行3次头删
DGRPopFront(Guard);
DGRPopFront(Guard);
DGRPopFront(Guard);
DGRPrint(Guard);
//再次进行3次头删,其中前两次完全删除,额外一次观察是否执行
DGRPopFront(Guard);
DGRPopFront(Guard);
DGRPopFront(Guard);
DGRPrint(Guard);
观察结果
Guard->4->5->Guard
Guard->Guard
中间结点——某结点前方插入(带结点查找函数Find)
在某个结点地址的前方插入一个新的双向结点,首先需要对该待插入位置的结点进行有效性检测,即检查该结点是否存在于待插入的链表中,定义查找链表中某个结点是否存在函数Find,并以布尔值返回,如果存在返回真,否则返回假。
查找链表结点函数
bool Find(DGR* Guard, DGR* pos) //1. 传入待查链表和位置
{
assert(Guard && pos); //2. 两者均不能为空指针,如果存在空指针则报错
DGR* cur = Guard->next; //3. 定义临时遍历指针,以链表首结点地址赋值
while (cur != Guard) //4. 当遍历指针不为哨兵结点地址时继续遍历
{
if (cur == pos) //5. 如果存在遍历的结点地址等价于待查结点地址,则存在
{
return true;
}
cur = cur->next;
}
return false; //6. 不存在则返回假
}
-
查找某结点是否于原链表中存在的意义是,如果传入一个待插入的链表结点地址,但是该结点不存在于原链表中,则不执行插入操作。而通过该函数证明确实存在该结点,才能直接通过传入的该结点地址的前驱指针进行结点的插入。
-
查找一个结点的时间复杂度为O(N),因为需要遍历双向链表,但是只要找到了该结点,对于该结点的插入或擦除操作的时间复杂度就是O(1)了。
-
如果传入的地址为头哨兵结点地址,则执行尾插操作,因为头哨兵结点的前驱指向原链表末节点地址,在哨兵的前方插入即相当于对于原链表插入新的末节点。而如果要进行头插,将pos地址置为原链表的首结点地址Guard->next即可,其他地方执行中间结点的前方插入即可。
原理图如下:
某结点前方插入函数
void DGRInsert(DGR* Guard, DGR* pos, DGREtype x)//前方插入
{
assert(Guard && pos);
if (pos == Guard) //1. 如果插入位置等于哨兵结点,则尾插
{
DGRPushBack(Guard, x);
}
else if (!Find(Guard, pos)) //2. 如果在链表中找不到待插入结点地址,则不插入
{
printf("插入失败,找不到待插入结点\n");
return;
}
else //3. 否则开辟新结点进行中间插入
{
DGR* NewNode = BuyListNode(x); //4. 开辟新结点
NewNode->next = pos; //5. 使新结点的后继指向待插入结点,前驱指向原结点前驱
NewNode->prev = pos->prev;
NewNode->prev->next = NewNode; //6. 使原前驱结点的后继指向该新插入的结点
pos->prev = NewNode; //7. 并让原位置结点的前驱也指向新结点
}
}
测试用例
//对于仅初始化的空链表进行中间插入
DGR* ExtraNode = BuyListNode(0); //定义一个不存在与原链表结点
DGRInsert(Guard, ExtraNode, 10); //1. 在原链表中寻找该不存在的结点插入
DGRInsert(Guard, Guard, 1); //2. 在头哨兵结点前插入1
DGRPrint(Guard);
DGRInsert(Guard, Guard->next, 2); //3. 在首结点前插入2
DGRPrint(Guard);
DGRInsert(Guard, Guard->prev, 3); //4. 在末节点前插入3
DGRPrint(Guard);
DGRInsert(Guard, Guard->next->next, 4); //5. 在第二个结点前插入4
DGRPrint(Guard);
观察结果
插入失败,找不到待插入结点
Guard->1->Guard
Guard->2->1->Guard
Guard->2->3->1->Guard
Guard->2->4->3->1->Guard
擦除函数
与中间插入函数不同的是,该算法擦除的结点不分前后位置,而仅擦除pos指向的结点本身,但这里要注意三种情况下不能擦除:
- 当链表为空时,也即Guard->next = Guard时,无法执行擦除功能。
- 当需要擦除的结点为头哨兵结点时,因为不是链表销毁函数,无法执行擦除功能。
- 当需要擦除的结点地址pos在原链表中无法定位找到时,无法执行擦除功能。
双向链表结点擦除函数
void DGRErase(DGR* Guard, DGR* pos)
{
assert(Guard && pos); //1. 断言判断哨兵地址和待擦除地址pos非空
if (Guard->next == Guard || pos == Guard || !Find(Guard, pos)) //2. 为以上3种情况的其中一种都拒绝执行擦除功能
{
printf("擦除失败,找不到待擦除结点\n");
return;
}
else //如果pos在链表中找到且符合擦除要求,则执行下列操作
{
pos->prev->next = pos->next; //3. 将待擦除结点的后继结点地址由前一结点的后继指针继承
pos->next->prev = pos->prev; //4. 将待擦除结点的前驱结点地址由后一结点的前驱指针继承
free(pos); //5. 将该结点pos释放
}
}
原理图如下:
☣️图中看起来似乎执行中间擦除的时间复杂度为O(N),但其实是调用Find查找验证pos结点存在的算法需要遍历链表,而实际上擦除结点和链接前后指针的时间复杂度为O(1),所以如果将查找步骤去掉,对已知的链表中结点进行直接擦除时,就可以很快得到擦除的结果而无需遍历。
测试用例
//对链表Guard1->2->3->4->5->6->Guard进行擦除操作
DGR* ExtraNode = BuyListNode(0);
DGRErase(Guard, ExtraNode); //Test1,删除非链表中的结点☣️
DGRErase(Guard, Guard); //Test2,删除哨兵结点☣️
DGRErase(Guard, Guard->prev); //Test3,删除末节点
DGRPrint(Guard);
DGRErase(Guard, Guard->prev->prev); //Test4,删除倒数第二个
DGRPrint(Guard);
DGRErase(Guard, Guard->next); //Test5,删除首结点
DGRPrint(Guard);
DGRErase(Guard, Guard->next->next); //Test6,删除第二个结点
DGRPrint(Guard);
DGRErase(Guard, Guard->next); //Test7,删除首结点
DGRPrint(Guard);
DGRErase(Guard, Guard->next); //Test8,删除首结点
DGRPrint(Guard);
DGRErase(Guard, Guard->next); //Test9,链表已为空,继续删除☣️
观察结果
擦除失败,找不到待擦除结点 //Test1☣️
擦除失败,找不到待擦除结点 //Test2☣️
Guard->1->2->3->4->5->Guard //Test3
Guard->1->2->3->5->Guard //Test4
Guard->2->3->5->Guard //Test5
Guard->2->5->Guard //Test6
Guard->5->Guard //Test7
Guard->Guard //Test8
擦除失败,找不到待擦除结点 //Test9☣️
修改函数
修改双向链表中的某个结点值大体思路与擦除结点相同,都是需要通过结点查找函数Find来验证结点是否存在于链表内部而进行修改,注意修改的结点地址不能为头哨兵结点,且链表也不能为空,待修改结点必须位于链表内部这三点满足才能进行结点数值域修改。
双向链表结点值修改函数
void DGRModify(DGR* Guard, DGR* pos, DGREtype x)
{
assert(Guard && pos);
if (Guard->next == Guard || pos == Guard || !Find(Guard, pos))
{
printf("修改失败,找不到待修改结点\n");
return;
}
else
{
pos->data = x; //若上述条件都不满足,则可以对结点数值进行修改,直接赋新值即可
}
}
测试用例
//定义链表结构待测试链表结构
DGRInsert(Guard, Guard, 1);
DGRInsert(Guard, Guard, 1);
DGRInsert(Guard, Guard, 1);
DGRInsert(Guard, Guard, 1);
DGRPrint(Guard);
//定义链表外带值结点
DGR* ExtraNode = BuyListNode(0);
//调用修改函数测试
DGRModify(Guard, Guard, 8); //Test1,修改哨兵结点值☣️
DGRModify(Guard, ExtraNode, 8); //Test2,修改链表外结点值☣️
DGRModify(Guard, Guard->next, 8); //Test3,修改首结点值
DGRPrint(Guard);
DGRModify(Guard, Guard->next->next, 8); //Test4,修改第二个结点值
DGRPrint(Guard);
DGRModify(Guard, Guard->prev->prev, 8); //Test5,修改第三个结点值
DGRPrint(Guard);
DGRModify(Guard, Guard->prev, 8); //Test6,修改末节点值
DGRPrint(Guard);
观察结果
//原链表结构
Guard->1->1->1->1->Guard
修改失败,找不到待修改结点 //Test1☣️
修改失败,找不到待修改结点 //Test2☣️
Guard->8->1->1->1->Guard //Test3
Guard->8->8->1->1->Guard //Test4
Guard->8->8->8->1->Guard //Test5
Guard->8->8->8->8->Guard //Test6
双向循环链表销毁
如果双向链表为空,直接将头哨兵结点释放。如果不为空,将除了哨兵结点之外的所有结点全部尾删(或头删)干净后,再释放哨兵结点即可。
双向链表销毁函数
void DGRDestroy(DGR* Guard)
{
assert(Guard);
if ((Guard)->next == Guard) //空链表,直接释放头结点
{
free(Guard);
}
else
{
while(Guard->next != Guard) //否则将其余链表结点循环尾删
{
DGRPopBack(Guard); //调用头删或擦除函数也可
}
free(Guard); //最后释放头哨兵结点
}
}
☣️需要注意的是,链表销毁函数只会将使用前初始化的头哨兵结点地址的空间释放,但不会自动置空,如果释放后不慎被其他函数继续调用,会传入野指针,从而引发程序崩溃错误,所以如上写法需要在销毁函数调用完成后在调用的函数外部手动置空,如下所示:
//将上例存有Guard->8->8->8->8->Guard的链表销毁
DGRDestroy(Guard);
Guard = NULL;
DGRPrint(Guard);
观察结果
手动置空后再调用打印函数即会报错,因为打印函数内部存在对哨兵结点的断言判空,因为在调用的函数已经被用户手动将释放的哨兵结点置空,所以不会再为其他链表函数所用,保证了指针和程序的安全性。
⭐后话
- 博客项目代码开源,获取地址请点击本链接:CSDN-带头双向循环链表 · VelvetShiki_Not_VS。
- 若阅读中存在疑问或不同看法欢迎在博客下方或码云中留下评论。
- 欢迎访问我的Gitee码云,如果对您有所帮助还可以一键三连,获取更多学习资料请关注我,您的支持是我分享的动力~