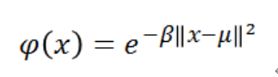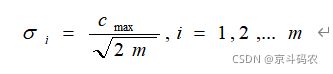【项目实战】Python实现基于RBF神经网络的半导体刻蚀机数据分析

说明：这是一个机器学习实战项目（附带数据+代码），如需数据+完整代码可以直接到文章最后获取。

1.项目背景

       对半导体刻蚀机进行故障诊断，首先需要采集获取半导体刻蚀机刻蚀过程的数据，并对数据进行分析和处理工作。本篇文章的半导体刻蚀机原始数据来自于LAM9600等离子刻蚀机加工晶元时的运行状态数据。本篇主要介绍半导体刻蚀机刻蚀过程数据前期的预处理工作，主要包括如下内容：半导体刻蚀机数据的分析、半导体刻蚀机故障数据的表现特征以及异常数据的提取，然后对半导体刻蚀机故障数据的提取和数据整合。通过数据预处理，得到了维数统一的故障数据集，为后面的分类设计和测试数据集的实验验证奠定基础。

      半导体制造过程的晶圆深度特征表示是晶圆数据异常检测的前提和基础。研究怎样利用深度学习理论设计深度神经网络架构，从非标记的原始晶圆数据中，非监督自主学习能表征健康状态特征，然后通过健康特征建立基线模型，对故障状态的数据集进行故障识别。

2.数据收集

数据集如下：

训练数据集：etch_train.csv

测试数据集：etch_test.csv

数据字段包括：Run ID、Time等

在实际应用中，根据自己的数据进行替换即可。

特征数据：除此数据项TCP Rfl Pwr之外的数据

标签数据：TCP Rfl Pwr

3.数据预处理

1）半导体刻蚀机故障分析

      半导体刻蚀机作为半导体制造中重要基础设备之一，其工作性能和制造的加工质量和生产效率有直接的影响。当半导体刻蚀机中有故障时，相关技术人员应对故障数据发生的设备点进行及时发现并正确的处理，以此来保证刻蚀设备运行的安全性，同时降低由于故障原因对刻蚀设备运行造成的影响。

       本文为了研究刻蚀过程数据驱动的异常检测方法，在实验性地刻蚀晶圆的过程中，引入了多种不同的故障，包括气体流量、卡盘压力等的人为改变等，一共 20 类。也就是说这20种不同的物理量都有可能引发刻蚀设备异常，而本次故障类型认定20种数据变化都会引起最终整条数据的故障。本次收集的数据中包含 19 个采自传感器的变量，1 个时间变量，2 个流程性变量，共 22 个变量。每个变量为一列，构成了训练与测试数据。每个变量的具体名称及其对应的含义如下表所示。

数据表头描述

序号	列名	数据含义
1	Run ID	晶元流水号
2	Time	时间
3	Step Number	制造工艺步骤
4	BCl3 Flow	过程物理量
5	Cl2 Flow
6	RF Btm Pwr
7	RF Btm Rfl Pwr
8	Endpt A
9	He Press
10	Pressure
11	RF Tuner
12	RF Load
13	RF Phase Err
14	RF Pwr
15	RF Impedance
16	TCP Tuner
17	TCP Phase Err
18	TCP Impedance
19	TCP Top Pwr
20	TCP Rfl Pwr
21	TCP Load
22	Vat Valve

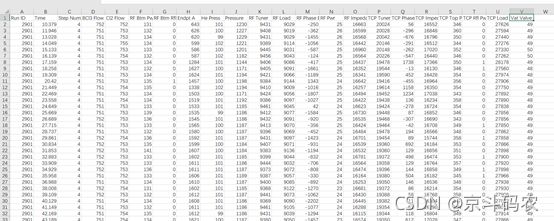
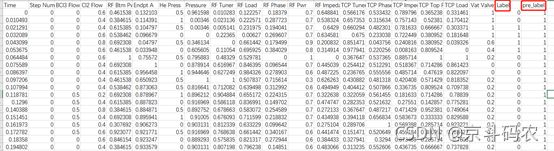
2）半导体刻蚀机数据分析

       本文中的半导体刻蚀机原始数据来源于LAM 9600等离子刻蚀机运行状态的部分数据改编。提供的采集数据以CSV文件的形式进行存放，并且以每个晶元为单位将刻蚀设备生产过程中产生的数据采集并存放在表格中。如图所示。

原始训练数据

       以第一行数据为例，代表编号为2901的晶元在时间点10.379分时第四工艺步骤的各个过程物理量。每个晶元每个步骤采集了近50条数据，训练数据集共采集了85个晶元的数据。总共计7608条数据。同样的测试数据集采集了31个晶元在刻蚀工艺步骤4、5的物理量数据，总共计5162条数据。

3）半导体刻蚀机故障数据提取

      本节的目的是为了从训练数据集和测试数据集中提取异常数据即故障数据，为后续数据分析和神经网络的读取做准备。在半导体刻蚀机数据中，故障数据相较于正常数据而言可以看作是异常波动数据，也就是误差较大的数据。目前筛选误差数据最常用的统计方法有：狄克逊准则(Dixon)、莱茵达准则(PanTa)、格拉布斯准则(Grubbs)、肖维勒准则(Chauvenet)等，这些方法中每种方法都有其自身的优点和缺点。数据的样本容量大于或等于50个时（本文所用的样本量已经大于50）我们选用莱茵达准则来剔除样本数据中的大误差数据是最好的选择，会得到一个较好效果。所以此次论文采用了莱茵达准则。

       此次论文采用莱茵达准则，对同一维数的数据求平均值和均方根偏差后，根据一定的准则范围来提取半导体刻蚀数据中的故障数据。我们求出平均值和均方根偏差后，可以运用莱茵达准则根据平均值和均方根偏差两个重要参数来确认出半导体刻蚀数据中的异常数据。莱茵达准则又被称为3σ 准则，是比较普遍易学的异常值判断与剔除方法，它是根据样本数据与所求均值和均方根偏差的差异来进行判断的。其具体的计算方法如下：

       如图以测试数据集晶元2915 的数据为例，计算其每一个变量数据的算术平均值、剩余误差和均方根误差，根据平均值和均方根偏差这两个参数提取出半导体刻蚀数据中的故障数据通过提取其数据集中的故障数据 。

       如图所示Pressure列中，均值为1232.537，均方根偏差为18.645，取值是0.7924，的值约为0.5，0.7924>0.5，所以确定晶元2915在步骤5物理量BCl3 Flow数据1309、1303、1303、1295、1296属于异常数据。

Pressure列的异常数据

      在示Pressure列中，取值为0.44，的值约为0.5，然而0.44<0.5，所以确定晶元2915在属于正常数据。

       就本次实验数据的分析而言，将含有故障数据的测试数据集按7：3的比例分为2份，分别命名为done数据集和done_test数据集，将故障标签设为0和1，0代表无故障，1代表有故障，通过莱茵达准则我们可以做出带有异常值数据的判别，并在其数据末端标出故障标签。如图为从done数据集提取的不良数据值截图，如图所示：

                                                  刻蚀机不良数据值

4）数据整合

       经故障提取后，数据的维数存在着较大的差异。不管是利用神经网络、深度学习，还是其他AI人工智能算法，大多数算法模型都无法很好地处理数据维度。为此，我们需要一种方法去实现一个自适应降维的过程，将对数据分析结果影响不大的维数除去，但是不会影响数据分析结果。

       通过数据差异较大的过程物理量的分析，我们将数据故障标签设定为0和1，0代表无故障，1代表有故障。因此我们可以将物理过程量RF Btm Rfl Pwr和TCP Rf1 Pwr作为数据差异项剔除，因为它的数据差异介于0，1之间，而故障标签也是0，1，所以将会对网络读取判断产生影响，故而将其剔除，训练数据读取时Run ID，Time和Step Number将不作为数据维数输入训练网络，因为它们的变化是固定的，所以最终输入网络的物理量有17种，故网络的输入维数为17。

      通过故障提取和数据整合后，整理出了网络训练的故障数据集。在故障数据和正常数据集的基础上，对其进行了维数整合处理，在在原有的训练数据集中加入一定数量的带有故障数据的数据集。将整合后的数据集作为神经网络训练的样本数据集，并对样本数据做标记，此时数据标为2种类型，即为0和1。如图所示：

 

关键代码展示：

 data_0 = pd.read_csv('etch_test.csv')  # 读取数据
    data_0.drop(['RF Btm Rfl Pwr', 'TCP Rfl Pwr'], axis=1, inplace=True)  # 去掉RF Btm Rfl Pwr TCP Rfl Pwr异常列值
    labellist = np.zeros(len(data_0['Run ID']))  # 生成0填充的数组
    results = []  # 定义一个空列表
    data = data_0.groupby('Run ID')  # 按照 Run ID 分组
    for key in set(data_0['Run ID'].tolist()):  # Run ID列去重，然后进行循环
        data_1 = data.get_group(key)  # 分组
        ColNames = data_1.columns.tolist()  # 获取所有列名
        print('---执行至' + str(key) + '号')  # 打印执行过程日志
        for j in ColNames:  # 循环列名
            df = data_1[j]  # 获取指定列数据
            ks_res = JisuanJun(df)  # 调用JisuanJun计算函数
            result = Suanfa(df, ks_res)  # 调用Suanfa计算函数
            # series中的 none 和 empty
            if result is not None and result.empty == False:  # 空值和NONE不一样
                # series键值对直接 items
                results.append(result.items())  # 键值对配对

    for i in results:  # 循环所有结果数据
        for key, value in i:  # 形成 key-value键值对形式
            labellist[key + 2] = 1  # 标签数据赋值
    data_0['Label'] = labellist  # 把标签数据赋值给data_0列表
    min_max_scaler = preprocessing.MinMaxScaler()  # 定义归一化函数
    # 标准化训练集数据
    for key in set(data_0['Run ID'].tolist()):  # Run ID列去重，然后进行循环
        data_1 = data.get_group(key)  # 分组
        ColNames = data_1.columns.tolist()  # 获取所有列名
        print('---执行至' + str(key) + '号')  # 打印执行过程日志
        for j in ColNames:  # 循环列名
            df = data_1[j]  # 获取指定列数据
            _range = np.max(df) - np.min(df)  # 计算每列的最大值减去最小值
            data_train_nomal = (df - np.min(df)) / _range  # 开始归一化数据
            data_1[j] = data_train_nomal  # 归一化数据赋值
    data_1.to_csv(r"test000.csv", mode='a', index=False)  # 保存标准化后的数据

4.RBF神经网络半导体刻蚀机故障诊断模型的构建  

1）模型概述

通过对相关学习算法和 RBF 神经网络基本结构的研究得知，要初步构建一个 RBF神经网络模型，需要考虑以下几个问题：

(1)确定RBF神经网络的输入层节点个数，也就相当于样本的输入维数；

(2)确定隐含层的各个参数，包括数据中心、宽度以及隐含层节点个数。

(3)确定RBF神经网络的输出层神经元个数以及隐含层节点和输出层节点的相互连接的权值。

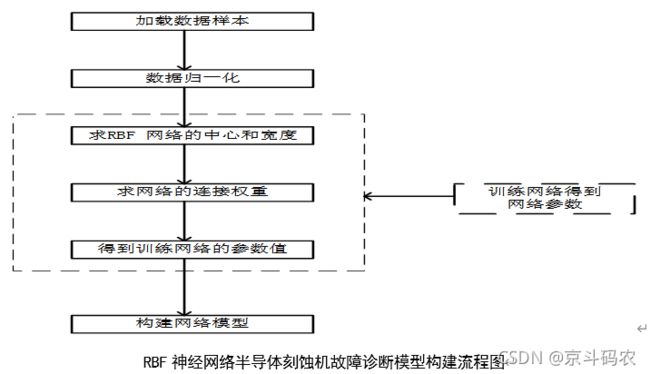
针对第 1 个问题，在第三章中已经得到了数据集，数据都是17维，因此RBF 神经网络的输入层节点设为17，并归一化处理。如下图所示，展示了构建基于 RBF 神经网络的半导体刻蚀机故障诊断模型的流程图。

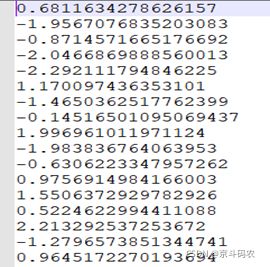
2）输入层数据归一化

数据归一化就是将数据经过某种算法或某种函数进行处理后，可以将所有数据限制在一定范围内使数据值缩小。归一化处理的好处是：一方面可以减低数据间存在的较大差距；另一方面还可以保证程序运行时收敛速度加快，对于RBF神经网络的训练而言，也会间接地影响训练网络的精度。 此次论文中采用快速简单的线性归一化转换原则，直接设定限制范围，将样本数据值限制在范围(-1，1)之间，具体公式如下：

 

归一化处理后的部分数据

       这样，去除对实验结果影响不大的编号，时间，工艺步骤，我们可以将RBF 神经网络的输入层的输入维数即为17，然后训练网络就可以对归一化处理后的样本进行直接读取，在这里我们将测试数据集按7:3分开，其中的70%用作网络的实验验证对比，30%用作网络的异常数据检测。

3）RBF神经元激活功能

       每个RBF神经元都会计算输入与其原型向量之间的相似度（从训练集中获取）。与原型更相似的输入向量返回的结果更接近于1。相似函数的选择可能不同，但最流行的是基于高斯模型。以下是具有一维输入的高斯方程。

 

       其中x是输入，mu是平均值，而sigma是标准偏差。这将产生下面所示的熟悉的钟形曲线，其中心位于平均值mu上（在下面的图中，平均值为5，sigma为1）。

 

RBF神经元激活功能略有不同，通常写为：

       在高斯分布中，mu表示分布的均值。在这里，它是原型矢量，它位于钟形曲线的中心。对于激活函数phi，我们对标准偏差sigma的值不直接感兴趣，因此我们进行了一些简化的修改。

       第一个变化是我们删除了外部系数1 /（sigma * sqrt（2 * pi））。该术语通常控制高斯的高度。但是，在这里，输出节点所施加的权重是多余的。在训练期间，输出节点将学习正确的系数或“权重”以应用于神经元的反应。第二个变化是我们用单个参数“ beta”替换了内部系数1 /（2 * sigma ^ 2）。该β系数控制钟形曲线的宽度。同样，在这种情况下，我们不在乎sigma的值，我们只是在乎是否存在控制钟形曲线宽度的系数。因此，我们通过用单个变量替换项来简化方程式。

4）RBF神经元激活可产生不同的beta值

       当我们将方程式应用到n维向量时，符号的表达也略有变化。激活方程式中的双杠符号表示我们正在x和mu之间的欧几里德距离，并将结果平方。对于一维高斯，这简化为（x-mu）^ 2。

       重要的是要注意，此处用于评估输入向量和原型之间的相似性的基本度量标准是两个向量之间的欧几里得距离。

       同样，当输入等于原型向量时，每个RBF神经元都会产生最大的响应。这允许将其作为相似性的度量，并对所有RBF神经元的结果求和。

       当我们从原型向量中移出时，响应呈指数下降。从RBFN架构说明中可以回忆起，每个类别的输出节点都采用网络中每个RBF神经元的加权总和，换句话说，网络中的每个神经元都会对分类决策产生一定的影响。然而，激活函数的指数下降意味着，其原型远离输入向量的神经元实际上对结果的贡献很小。

5）隐含层节点参数设计

       网络隐含层参数主要包括三个重要参数：径向基函数的中心、隐含层节点个数和宽度。在 K-means 算法中聚类个数 K 值的设置与隐含层节点个数的设置有相互依赖的关系，聚类类别 K 即为网络模型中隐含层的节点个数。

       K-means 算法的基本思想：对于数据样本集而言，通过判定样本间的距离，将样本集中的数据划分成 K 类。在这 K 类中，我们可以选择将17变量中每一类变量中占比比较大的作为正常值，尽量让每类中的样本间距离最小，让正常的数据聚在一起作为一类，自然异常的数据相应位于群落之外，同时让 K 个类别间的距离尽量大，距离尽量大为了让网络更加容易识别正常数据与异常数据。

K-means 算法的基本步骤如下：

(1)从输入的样本数据中，随机选取 K 个对象作为开始的聚类中心，初始阶段我们选取的K自然为17；

(2)计算每个数据对象到各聚类中心的距离，这里直接使用的是坐标上2点间的距离公式计算，并根据计算的结果将其化归到最近的聚类中，距离什么类别最近就将这个数据值归类到哪一种类别；

(3)重新计算各聚类的中心；

(4)重复②，③步骤，直到聚类的中心不再变化或是小于设定的某一阈值，表明该算法结束。

      经过训练后，得到网络的最终中心之间最大距离为238.328，介于维数Bcl3 Flow与Rf  Phase Err的聚类中心之间，通过 k-means 算法求出中心距离后，进一步确定网络的宽度Speard，求解公式为：

       m 表示训练样本的个数，为所选取中心之间的最大距离。最终确定网络宽度为2，通过网络训练不断的迭代和数据的收敛可以得到网络的神经元数目为600，而网络的中心值基于python程序编写的，它不作为返回值，相当于各类参数的值不是唯一确定的它是基于网络训练的最佳效果而确定。 

6）输出层设计

      输出层的参数设置主要包括隐含层与输出层的连接权重值（基于python的RBF神经网络实现没有返回权重值）以及输出层的节点个数。在本文半导体刻蚀机故障共有17类，对应数据集中的17类数据。

       最后一组参数是输出权重。可以使用梯度下降（也称为最小均方）进行训练。首先，对于训练集中的每个数据点，计算RBF神经元的激活值。这些激活值成为梯度下降的训练输入。线性方程需要一个偏置项，因此我们总是将固定值“ 1”添加到激活值矢量的开头。必须为每个输出节点（即，数据集中的每个类）分别运行渐变下降。对于输出标签，对于与输出节点属于同一类别的样本，请使用值“ 1”，对于所有其他样本，请使用值“ 0”。例如，如果我们的数据集具有三个类别，并且我们正在学习输出节点3的权重，则所有类别3示例应标记为“ 1”，所有类别1和2示例应标记为0。

        当 RBF 神经网络的中心、宽度与权重确定后，训练得到该网络模型的输出结果如图 4.3所示。图中每一行代表选取数据经归一化后的输出结果。

                                             网络center值 

网络delta值 

             网络weight值

关键代码展示：

def load_data(file_name): # 定义函数
    # 获取特征和标签数据，然后以矩阵形式返回
    file = open(file_name)  # 打开文件
    feature_data = []  # 定义一个特征空列表
    label0 = []  # 定义一个标签空列表
    for line in file.readlines(): # 循环读取每行数据
        feature_tmp = [] # 定义一个临时空列表
        lines = line.strip().split("\t") # 以空格拆分数据
        for i in range(len(lines) - 1):
            data = float(lines[i]) / 1000  # 每行数据除以1000
            feature_tmp.append(data) # 处理后的数据加入临时列表
        label0.append(int(lines[-1])) # 处理后的数据加入标签列表
        feature_data.append(feature_tmp) # 处理后的数据加入特征列表
    file.close()  # 关闭文件
    n_output = 1  # 定义n_output为常熟1

    return mat(feature_data), mat(label0).transpose(), n_output   # 以矩阵形式输出特征、标签数据


def hanshu(x): # 定义函数

    return x   # 实现输出出层神经元激活函数的返回


def hidden_out(feature, center, delta):  # 定义函数
    '''
    实现rbf函数（隐含层神经元输出函数）
    input:feature(mat):数据特征
          center(mat):rbf函数中心
          delta(mat)：rbf函数扩展常数
   最后隐含层输出
    '''
    m, n = shape(feature)  # 获取特征的形状
    m1, n1 = shape(center)  # 获取rbf函数中心的形状
    hidden_out = mat(zeros((m, m1)))  # 获取隐藏层输出
    for i in range(m):  # 循环特征数据
        for j in range(m1): # 循环rbf函数中心数据
            hidden_out[i, j] = exp(-1.0 * (feature[i, :] - center[j, :]) * (feature[i, :] - center[j, :]).T / (
                    2 * delta[0, j] * delta[0, j]))   # 隐藏层函数计算
    return hidden_out   # 隐藏层计算输出


def predict_in(hidden_out, w): # 定义预测函数
    '''
    计算输出层的输入
    input:  hidden_out(mat):隐含层的输出
            w1(mat):隐含层到输出层之间的权重
            b1(mat):隐含层到输出层之间的偏置
    output: predict_in(mat):输出层的输入
    '''
    m = shape(hidden_out)[0]  # 获取隐藏层形状
    print('获取隐藏层形状')
    print(m)
    predict_in = hidden_out * w  # 隐藏层乘以权重
    return predict_in   # 返回结果


def predict_out(predict_in):  # 定义函数
    '''输出层的输出
    input:  predict_in(mat):输出层的输入
    output: result(mat):输出层的输出
    '''
    n = len(predict_in)  # 获取predict_in的长度
    result = hanshu(predict_in) # 调用hanshu函数进行计算
    result[0:n // 4] = 1  # 结果赋值
    result[n // 4::] = 0.084 # 结果赋值
    return result   # 返回结果

def predict_test(predict_in): # 定义函数
    '''测试数据输出层的输出
    input:  predict_in(mat):输出层的输入
    output: result(mat):输出层的输出
    '''
    n = len(predict_in)  # 获取predict_in的长度
    result = hanshu(predict_in) # 调用hanshu函数进行计算
    result[0:n // 4] = 1  # 结果赋值
    result[n // 4::] = 0  # 结果赋值
    return result   # 返回结果


def rbf_train(feature, label, n_hidden, maxCycle, alpha, n_output): # 定义训练函数
    '''
    计算隐含层的输入
    input:  feature(mat):特征
            label(mat):标签
            n_hidden(int):隐含层的节点个数
            maxCycle(int):最大的迭代次数
            alpha(float):学习率
            n_output(int):输出层的节点个数
    output: center(mat):rbf函数中心
            delta(mat):rbf函数扩展常数
            w(mat):隐含层到输出层之间的权重
    '''
    m, n = shape(feature)  # 获取特征形状
    # 初始化函数中心、权重、函数扩展常数
    center = mat(random.rand(n_hidden, n))  # rbf函数中心数据转换成矩阵形式
    center = center * (8.0 * sqrt(6) / sqrt(n + n_hidden)) - mat(ones((n_hidden, n))) * (
            4.0 * sqrt(6) / sqrt(n + n_hidden))  # 初始化rbf函数中心
    delta = mat(random.rand(1, n_hidden)) # rbf函数扩展常数转换成矩阵形式
    delta = delta * (8.0 * sqrt(6) / sqrt(n + n_hidden)) - mat(ones((1, n_hidden))) * (
            4.0 * sqrt(6) / sqrt(n + n_hidden)) #  初始化rbf函数扩展常数
    w = mat(random.rand(n_hidden, n_output)) # 隐含层到输出层之间的权重转换成矩阵形式
    w = w * (8.0 * sqrt(6) / sqrt(n_hidden + n_output)) - mat(ones((n_hidden, n_output))) * (
            4.0 * sqrt(6) / sqrt(n_hidden + n_output)) # 初始化隐含层到输出层之间的权重

    # 训练
    iter = 0 #定义初始化迭代
    while iter <= maxCycle: # 增加判断，如果迭代次数大于maxCycle，则停止循环
        # 信号正向传播
        hidden_output = hidden_out(feature, center, delta) # 调用hidden_out函数，计算隐含层的输出

        output_in = predict_in(hidden_output, w)  # 调用predict_in函数，计算输出层的输入

        output_out = predict_out(output_in)  # 调用predict_out函数，计算输出层的输出

        # 误差的反向传播
        error = mat(label - output_out) # 计算反向误差
        for j in range(n_hidden): # 循环隐藏层
            sum1 = 0.0 # 定义初始化数值
            sum2 = 0.0 # 定义初始化数值
            sum3 = 0.0 # 定义初始化数值
            for i in range(m):  # 循环特征数据
                sum1 += error[i, :] * exp(
                    -1.0 * (feature[i] - center[j]) * (feature[i] - center[j]).T / (2 * delta[0, j] * delta[0, j])) * (
                                feature[i] - center[j]) # 计算rbf函数中心，进行初步计算
                sum2 += error[i, :] * exp(
                    -1.0 * (feature[i] - center[j]) * (feature[i] - center[j]).T / (2 * delta[0, j] * delta[0, j])) * (
                                feature[i] - center[j]) * (feature[i] - center[j]).T  # 计算rbf函数扩展常数，进行初步计算
                sum3 += error[i, :] * exp(
                    -1.0 * (feature[i] - center[j]) * (feature[i] - center[j]).T / (2 * delta[0, j] * delta[0, j])) # 计算隐含层到输出层之间的权重
            delta_center = (w[j, :] / (delta[0, j] * delta[0, j])) * sum1  # 计算rbf函数中心，进行最终计算
            delta_delta = (w[j, :] / (delta[0, j] * delta[0, j] * delta[0, j])) * sum2 # 计算rbf函数扩展常数，进行最终计算
            delta_w = sum3  # 权重赋值
            # 修正权重和rbf函数中心和扩展常数
            center[j, :] = center[j, :] + alpha * delta_center  # 修正rbf函数中心
            delta[0, j] = delta[0, j] + alpha * delta_delta # 修正rbf扩展常数
            w[j, :] = w[j, :] + alpha * delta_w #  修正隐含层到输出层之间的权重
        if iter % 10 == 0:  # 进行迭代判断
            cost = (1.0 / 2) * get_loss(get_predict(feature, center, delta, w) - label)  # 调用get_loss函数，进行损失计算
            print("\t-------- iter: ", iter, " ,cost: ", cost) # 打印损失的计算日志
        if cost < 15:  #  如果损失函数值小于15则停止迭
            break
        iter += 1
    return center, delta, w  # 返回rbf函数中心、rbf扩展常数、隐含层到输出层之间的权重


def get_loss(cost):  # 定义损失函数
    '''
    计算当前损失函数的值
    input:  cost(mat):预测值与标签之间的差
    output: cost_sum / m (double):损失函数的值
    '''
    m, n = shape(cost)  # 获取cost的形状

    cost_sum = 0.0  # 初始化赋值
    for i in range(m):  # 循环数据
        for j in range(n): # 循环数据
            cost_sum += cost[i, j] * cost[i, j]  # 进行损失计算
    return cost_sum / 2  # 返回损失

 5.模型评估

1）准确率

编号	数据集	准确率
1	训练集	76.84%
2	测试集	76.34%

6.实际应用

基于模拟和真实数据的结果表明，神经网络在预测精度方面取得良好的效果。在实际半导体刻蚀机故障诊断中，可以参考此模型的诊断数据。测试集预测结果如下：

本次机器学习项目实战所需的资料，项目资源如下： 【项目实战】Python实现基于RBF神经网络的半导体刻蚀机数据分析-Python文档类资源-CSDN下载