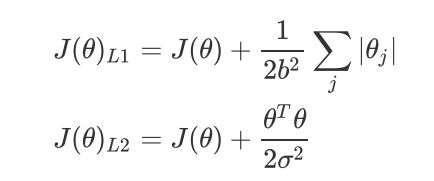《菜菜的机器学习sklearn课堂》逻辑回归

• • 二元逻辑回归的损失函数
• • 损失函数的概念与解惑

• 重要参数penalty & C

• • 正则化（L1、L2）

• 附录

• • 逻辑回归的参数列表

• 逻辑回归的属性列表

• 逻辑回归的接口列表

[《菜菜的机器学习sklearn课堂》笔记目录 + 课件](()

[](()概述：名为"回归"的分类器

================================================================================

我们已经接触了不少带 “回归” 二字的算法，例如回归树、随机森林的回归，他们都是区别于分类算法，用来处理和预测连续型标签的算法。然而逻辑回归是一种名为"回归"的线性分类器，其本质是由线性回归变化而来的，一种广泛使用于分类问题中的广义回归算法。

要理解逻辑回归从何而来，得先理解线性回归。线性回归是机器学习中最简单的的回归算法：

z = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n z = \theta_0 + \theta_1x_1 + \theta_2x_2 + … + \theta_nx_n z=θ0​+θ1​x1​+θ2​x2​+…+θn​xn​

θ \theta θ被统称为模型的参数，其中 θ 0 \theta_0 θ0​被称为截距(intercept)， θ 1 \theta_1 θ1​~ θ n \theta_n θn​被称为系数(coefficient)。这个表达式和我们熟悉的 y = k x + b y = kx + b y=kx+b是同样的性质。我们可以使用矩阵来表示这个方程，其中x和 θ \theta θ都可以被看做是一个列矩阵，则有：

z = [ θ 0 , θ 1 , θ 2 . . . θ n ] ∗ [ x 0 x 1 x 2 . . x n ] = θ T x ( x 0 = 1 ) z = [\theta_0, \theta_1, \theta_2…\theta_n] * \begin{bmatrix} x_0\\ x_1\\ x_2\\ …\\ x_n\\ \end{bmatrix} = \theta^Tx(x_0=1) z=[θ0​,θ1​,θ2​…θn​]∗⎣⎢⎢⎢⎢⎡​x0​x1​x2​…xn​​⎦⎥⎥⎥⎥⎤​=θTx(x0​=1)

线性回归的任务：构造一个预测函数 z z z来映射输入的特征矩阵x和标签值y的线性关系

• 构造预测函数的核心就是找出模型的参数： θ T \theta^T θT和 θ 0 \theta_0 θ0​

著名的最小二乘法就是用来求解线性回归中参数的数学方法

通过函数 z z z ，线性回归使用输入的特征矩阵X来输出一组连续型的标签值y_pred，以完成各种预测连续型变量的任务（比如预测产品销量，预测股价等等）。

如果我们的标签是离散型变量（尤其是满足0-1分布的离散型变量），要怎么办呢？

我们可以通过引入联系函数(link function)，将线性回归方程 z z z变换为 g ( z ) g(z) g(z)，并且令 g ( z ) g(z) g(z)的值分布在(0,1)之间，且当 g ( z ) g(z) g(z)接近0时样本的标签为类别0，当 g ( z ) g(z) g(z)接近1时样本的标签为类别1，这样就得到了一个分类模型。而这个联系函数对于逻辑回归来说，就是Sigmoid函数：

g ( z ) = 1 1 + e − z g(z) = \frac 1 {1 + e^{-z}} g(z)=1+e−z1​

面试高频问题：Sigmoid函数的公式和性质

Sigmoid函数能够将任何实数映射到(0,1)区间，使其可用于将任意值函数转换为更适合二分类的函数。

因为这个性质，Sigmoid函数也被当作是归一化的一种方法，与我们之前学过的MinMaxSclaer同理，是属于数据预处理中的"缩放"功能，可以将数据压缩到[0,1]之内。区别在于，MinMaxScaler归一化之后是可以取到0和1的（最大值归一化后是1，最小值归一化后是0），但Sigmoid函数只是无限趋近于0和1。

线性回归中 z = θ T z = \theta^T z=θT，于是我们将 z z z带入，就得到了二元逻辑回归模型的一般形式：

g ( z ) = y ( x ) = 1 1 + e − θ T x g(z) = y(x) = \frac 1 {1 + e^{-\thetaTx}} g(z)=y(x)=1+e−θTx1​

y ( x ) y(x) y(x)就是我们逻辑回归返回的标签值。此时， y ( x ) y(x) y(x)的取值都在[0,1]之间，因此 y ( x ) y(x) y(x)和 1 − y ( x ) 1-y(x) 1−y(x)相加必然为1。如果我们令 y ( x ) y(x) y(x)除以 1 − y ( x ) 1-y(x) 1−y(x)可以得到 形似几率(odds) 的 y ( x ) 1 − y ( x ) \frac{y(x)}{1-y(x)} 1−y(x)y(x)​，在此基础上取对数，可以很容易就得到：

不难发现， y ( x ) y(x) y(x)的形似几率取对数的本质其实就是我们的线性回归 z z z，我们实际上是在对线性回归模型的预测结果取对数几率来让其的结果无限逼近0和1。因此，其对应的模型被称为 “对数几率回归”(logistic Regression)，也就是逻辑回归，这个名为"回归" 《一线大厂Java面试题解析+后端开发学习笔记+最新架构讲解视频+实战项目源码讲义》无偿开源 威信搜索公众号【编程进阶路】 却是用来做分类工作的分类器。

线性回归的核心任务是通过求解 θ \theta θ构建 z z z这个预测函数，并希望预测函数 z z z能够尽量拟合数据。因此，逻辑回归的核心任务也是类似的：求解 θ \theta θ来构建一个能够尽量拟合数据的预测函数 y ( x ) y(x) y(x)，并通过向预测函数中输入特征矩阵来获取相应的标签值y。

思考：y(x)代表了样本为某一类标签的概率吗？

[](()为什么需要逻辑回归?

---

在我们的各种机器学习经典书目中，周志华的《机器学习》400页仅有一页纸是关于逻辑回归的（还是一页数学公式），《数据挖掘导论》和《Python数据科学手册》中完全没有逻辑回归相关的内容，sklearn中对比各种分类器的效应也不带逻辑回归

无论机器学习领域如何折腾，逻辑回归依然是一个受热爱、使用广泛的模型，因为其优点：

1. 逻辑回归对线性关系的拟合效果好到丧心病狂

特征与标签之间的线性关系极强的数据，比如金融领域中的信用卡欺诈，评分卡制作，电商中的营销预测等等相关的数据，都是逻辑回归的强项。虽然现在有了梯度提升树GDBT，比逻辑回归效果更好，也被许多数据咨询公司启用，但逻辑回归在金融领域，尤其是银行业中的统治地位依然不可动摇（相对的，逻辑回归在非线性数据的效果很多时候比瞎猜还不如，所以如果你已经知道数据之间的联系是非线性的，千万不要迷信逻辑回归）

2. 逻辑回归计算快

对于线性数据，逻辑回归的拟合和计算都非常快，计算效率优于SVM和随机森林

3. 逻辑回归返回的分类结果不是固定的0和1，而是以小数形式呈现的类概率数字

我们因此可以把逻辑回归返回的结果当成连续型数据来利用。比如在评分卡制作时，我们不仅需要判断客户是否会违约，还需要给出确定的"信用分"，而这个信用分的计算就需要使用类概率计算出的对数几率，而决策树和随机森林这样的分类器，可以产出分类结果，却无法帮助我们计算分数（当然，在sklearn中决策树也可以产生概率，使用接口predict_proba调用就好，但一般来说，正常的决策树没有这个功能）。

4. 逻辑回归还有抗噪能力强的优点

福布斯杂志在讨论逻辑回归的优点时，甚至有着"技术上来说，最佳模型的AUC面积低于0.8时，逻辑回归非常明显优于树模型"的说法。逻辑回归在小数据集上表现更好，在大型的数据集上，树模型有着更好的表现。

逻辑回归的本质是一个返回对数几率的，在线性数据上表现优异的分类器，它主要被应用在金融领域。其数学目的是求解能够让模型对数据拟合程度最高的参数 θ \theta θ的值，以此构建预测函数 y ( x ) y(x) y(x)，然后将特征矩阵输入预测函数来计算出逻辑回归的结果y。

虽然我们熟悉的逻辑回归通常被用于处理二分类问题，但逻辑回归也可以做多分类。

[](()sklearn中的逻辑回归

---

| 逻辑回归相关的类 | 说明 |

| — | — |

| linear_model.LogisticRegression | 逻辑回归分类器（又叫logit回归，最大熵分类器） |

| linear_model.LogisticRegressionCV | 带交叉验证的逻辑回归分类器 |

| linear_model.logistic_regression_path | 计算Logistic回归模型以获得正则化参数的列表 |

| linear_model.SGDClassifier | 利用梯度下降求解的线性分类器（SVM，逻辑回归等等） |

| linear_model.SGDRegressor | 利用梯度下降最小化正则化后的损失函数的线性回归模型 |

| metrics.log_loss | 对数损失，又称逻辑损失或交叉熵损失 |

| 【 在sklearn0.21版本中即将被移除】 | |

| — | — |

| linear_model.RandomizedLogisticRegression | 随机的逻辑回归 |

| 其他会涉及的类 | 说明 |

| — | — |

| metrics.confusion_matrix | 混淆矩阵，模型评估指标之一 |

| metrics.roc_auc_score | ROC曲线，模型评估指标之一 |

| metrics.accuracy_score | 精确性，模型评估指标之一 |

[](()linear_model.LogisticRegression

===================================================================================================

class sklearn.linear_model.LogisticRegression (

penalty=‘l2’,

dual=False,

tol=0.0001,

C=1.0,

fit_intercept=True,

intercept_scaling=1,

class_weight=None,

random_state=None,

solver=‘warn’,

max_iter=100,

multi_class=‘warn’,

verbose=0,

warm_start=False,

n_jobs=None

)

[](()二元逻辑回归的损失函数

---

[](()损失函数的概念与解惑

在学习决策树和随机森林时，我们曾经提到过两种模型表现：

• 在训练集上的表现

• 在测试集上的表现

我们建模是追求模型在测试集上的表现最优，因此模型的评估指标往往是用来衡量模型在测试集上的表现的。

然而，逻辑回归有着基于训练数据求解参数 θ \theta θ的需求，并且希望训练出来的模型能够尽可能地拟合训练数据，即模型在训练集上的预测准确率越靠近100%越好。

因此，我们使用"损失函数"这个评估指标，来衡量参数为θ的模型拟合训练集时产生的信息损失的大小，并以此衡量参数θ的优劣。如果用一组参数建模后，

• 模型在训练集上表现良好

那我们就说模型拟合过程中的损失很小，损失函数的值很小，这一组参数就优秀

• 模型在训练集上表现糟糕

损失函数就会很大，模型就训练不足，效果较差，这一组参数也就比较差

即是说，我们在求解参数 θ \theta θ时，追求损失函数最小，让模型在训练数据上的拟合效果最优，即预测准确率尽量靠近100%。

关键概念：损失函数

衡量参数 θ \theta θ的优劣的评估指标，用来求解最优参数的工具

损失函数小，模型在训练集上表现优异，拟合充分，参数优秀

损失函数大，模型在训练集上表现差劲，拟合不足，参数糟糕

我们追求：能够让损失函数最小化的参数组合

注意：没有"求解参数"需求的模型没有损失函数，比如KNN，决策树

逻辑回归的损失函数是由极大似然估计推导出来的，具体结果可以写作：

J ( θ ) = − ∑ i = 1 m ( y i ∗ l o g ( y θ ( x i ) ) + ( 1 − y i ) ∗ l o g ( 1 − y θ ( x i ) ) ) ) J(\theta) = - \sum _{i=1} ^m (y_i * log(y_\theta(x_i)) + (1-y_i) * log(1-y_\theta(x_i)))) J(θ)=−i=1∑m​(yi​∗log(yθ​(xi​))+(1−yi​)∗log(1−yθ​(xi​))))

其中， θ \theta θ表示求解出来的一组参数，m是样本的个数， y i y_i yi​是样本i上真实的标签， y θ ( x i ) y_\theta(x_i) yθ​(xi​)是样本i上，基于参数 θ \theta θ计算出来的逻辑回归返回值， x i x_i xi​是样本i各个特征的取值。我们的目标就是求解出使 J ( θ ) J(\theta) J(θ)最小的 θ \theta θ取值。

注意，在逻辑回归的本质函数y(x)里，特征矩阵x是自变量，参数是 θ \theta θ。但在损失函数中，参数 θ \theta θ是损失函数的自变量，x和y都是已知的特征矩阵和标签，相当于是损失函数的参数。不同的函数中，自变量和参数各有不同，因此大家需要在数学计算中，尤其是求导的时候避免混淆。

由于我们追求损失函数的最小值，让模型在训练集上表现最优，可能会引发另一个问题：如果模型在训练集上表示优秀，却在测试集上表现糟糕，模型就会过拟合。虽然逻辑回归和线性回归是天生欠拟合的模型，但我们还是需要控制过拟合的技术来帮助我们调整模型，对逻辑回归中过拟合的控制，通过正则化来实现。

[](()重要参数penalty & C

---

[](()正则化（L1、L2）

正则化是用来防止模型过拟合的过程，常用的有L1正则化和L2正则化两种选项，分别通过在损失函数后加上参数向量 θ \theta θ的L1范式和L2范式的倍数来实现，这个增加的范式，被称为"正则项"，也被称为"惩罚项"。

损失函数改变，基于损失函数的最优化来求解的参数取值必然改变，我们以此来调节模型拟合的程度

• L1范式表现为参数向量中的每个参数的绝对值之和

J ( θ ) L 1 = C ∗ J ( θ ) + ∑ j = 1 n ∣ θ j ∣ ( j ≥ 1 ) J(\theta)_{L1} = C * J(\theta) + \sum_{j=1}^{n} |\theta_j | (j \ge 1) J(θ)L1​=C∗J(θ)+j=1∑n​∣θj​∣(j≥1)

• L2范数表现为参数向量中的每个参数的平方和的开方值。

J ( θ ) L 2 = C ∗ J ( θ ) + ∑ j = 1 n ( θ j ) 2 ( j ≥ 1 ) J(\theta)_{L2} = C * J(\theta) + \sqrt{\sum_{j=1}^n(\theta_j)2}(j \ge 1) J(θ)L2​=C∗J(θ)+j=1∑n​(θj​)2 ​(j≥1)

• J ( θ ) J(\theta) J(θ) - 损失函数

• C - 用来控制正则化程度的超参数

• n - 方程中特征的总数，也是方程中参数的总数

• j - 每个参数

在这里j要大于等于1，因为我们的参数向量 θ \theta θ中，第一个参数是 θ 0 \theta_0 θ0​是截距，它通常不参与正则化。

在许多书籍和博客中，大家可能也会见到如下的写法：

其实和我们上面的式子的本质是一模一样的。不过在大多数教材和博客中，常数项是乘以正则项，通过调控正则项来调节对模型的惩罚。而sklearn当中，常数项C是在损失函数的前面，通过调控损失函数本身的大小，来调节对模型的惩罚。