机器学习算法 09 —— EM算法(马尔科夫算法HMM前置学习,EM用硬币案例进行说明)
文章目录
- 系列文章
- EM算法
- 1 初识EM算法
- 2 EM算法介绍
-
- 2.1 最大似然估计
- 2.2 EM算法实例描述
- 2.3 EM算法流程
- 3 EM算法实例
-
- 3.1 一个简单案例
- 3.2 加入隐变量z后的求解
- 3.3 EM初级版
- 3.4 EM进阶版
系列文章
机器学习算法 01 —— K-近邻算法(数据集划分、归一化、标准化)
机器学习算法 02 —— 线性回归算法(正规方程、梯度下降、模型保存)
机器学习算法 03 —— 逻辑回归算法(精确率和召回率、ROC曲线和AUC指标、过采样和欠采样)
机器学习算法 04 —— 决策树(ID3、C4.5、CART,剪枝,特征提取,回归决策树)
机器学习算法 05 —— 集成学习(Bagging、随机森林、Boosting、AdaBost、GBDT)
机器学习算法 06 —— 聚类算法(k-means、算法优化、特征降维、主成分分析PCA)
机器学习算法 07 —— 朴素贝叶斯算法(拉普拉斯平滑系数、商品评论情感分析案例)
机器学习算法 08 —— 支持向量机SVM算法(核函数、手写数字识别案例)
机器学习算法 09 —— EM算法(马尔科夫算法HMM前置学习,EM用硬币案例进行说明)
机器学习算法 10 —— HMM模型(马尔科夫链、前向后向算法、维特比算法解码、hmmlearn)
EM算法
学习目标:
- 了解什么是EM算法
- 知道极⼤似然估计
- 知道EM算法实现流程
1 初识EM算法
EM算法即期望最大化(Exception-Maximum)算法,它是一个基础算法,是很多机器学习领域算法的基础,例如后面要学的马尔科夫算法(HMM)。
EM算法采取一种迭代优化策略,它的计算方法中每一次迭代都分为两步:期望步(E步)、极大步(M步),所以被称为EM算法。
EM算法受到缺失思想影响,最初是为了解决数据缺失情况下的参数估计问题,其基本思想是:
- 先根据已经给出的观测数据,估计出模型参数的值
- 然后根据参数值估计缺失数据的值,接着根据缺失数据和观测数据再次对模型参数值进行估计
- 之后就反复迭代,直到最后收敛,迭代才结束
2 EM算法介绍
想清晰的了解EM算法,我们需要知道⼀个基础知识: 概率论中的”极大似然估计“
2.1 最大似然估计
假如我们需要调查学校的男⽣和⼥⽣的身⾼分布 ,我们抽取100个男⽣和100个⼥⽣,将他们按照性别划分为两组。然后,统计抽样得到100个男⽣的身⾼数据和100个⼥⽣的身⾼数据。
如果我们知道他们的身⾼服从正态分布,但是这个分布的均值 μ \mu μ 和⽅差 δ 2 \delta^2 δ2是不知道,这两个参数就是我们需要估计的。
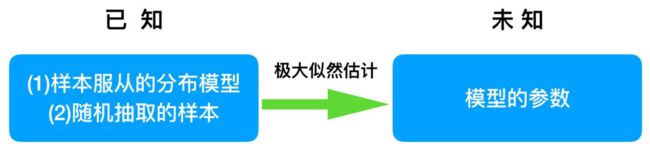
问题:我们知道样本所服从的概率分布模型和⼀些样本,我们需要求解该模型的参数。
我们已知的条件有两个:样本服从的分布模型、随机抽取的样本。 根据已知条件,通过极⼤似然估计,求出未知参数。
总的来说:最大似然估计就是⽤来估计模型参数的统计学⽅法。
问题数学化:
-
样本集 X = { x 1 , x 2 , . . . x n } , n = 100 X=\{x_1,x_2,...x_n\}, n=100 X={x1,x2,...xn},n=100
-
P ( x i ∣ θ ) P(x_i|\theta) P(xi∣θ)是抽到第i个男生的概率
-
由于100个样本之间独⽴同分布,所以同时抽到这100个男⽣的概率是它们各⾃概率的乘积,也就是样本集X中各个样本的联合概率,⽤下式表示:
L ( θ ) = L ( x 1 , x 2 , . . . , x n ; θ ) = Π i = 1 n p ( x i ; θ ) , θ ∈ Θ L(\theta)=L(x_1,x_2,...,x_n;\theta)=\Pi_{i=1}^n p(x_i;\theta),\theta \in \Theta L(θ)=L(x1,x2,...,xn;θ)=Πi=1np(xi;θ),θ∈Θ -
这个概率反映了在概率密度函数的参数是 θ \theta θ时,得到X这组样本的概率
-
我们需要找到⼀个参数θ,使得抽到X这组样本的概率最⼤,也就是说需要其对应的似然函数 L ( θ ) L(\theta) L(θ)最⼤。满⾜条件的 θ \theta θ叫做 θ \theta θ的最⼤似然估计值,记为:
θ ^ = a r g m a x L ( θ ) \hat{\theta}=arg\ max L(\theta) θ^=arg maxL(θ)
最大似然函数估计值求解步骤
-
首先写出似然函数: L ( θ ) = L ( x 1 , x 2 , . . . , x n ; θ ) = Π i = 1 n p ( x i ; θ ) , θ ∈ Θ L(\theta)=L(x_1,x_2,...,x_n;\theta)=\Pi_{i=1}^n p(x_i;\theta),\theta \in \Theta L(θ)=L(x1,x2,...,xn;θ)=Πi=1np(xi;θ),θ∈Θ
-
接着对似然函数取对数: l ( θ ) = l n L ( θ ) = l n Π i = 1 n p ( x i ; θ ) = Π i = 1 n l n p ( x i ; θ ) , θ ∈ Θ l(\theta)=lnL(\theta)=ln\Pi_{i=1}^n p(x_i;\theta)=\Pi_{i=1}^n lnp(x_i;\theta),\theta \in \Theta l(θ)=lnL(θ)=lnΠi=1np(xi;θ)=Πi=1nlnp(xi;θ),θ∈Θ
-
然后对上式求导,令导数为0,得到似然方程
-
最后,解似然方程
2.2 EM算法实例描述
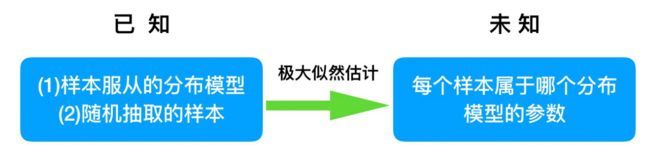
我们⽬前有100个男⽣和100个⼥⽣的身⾼,但是我们不知道这200个数据中哪个是男⽣的身⾼,哪个是⼥⽣的身⾼,即抽取得到的每个样本不知道是从哪个分布中抽取的。
这个时候,对于每个样本,就有两个未知量需要估计:
(1)这个身⾼数据是来⾃于男⽣数据集合还是来⾃于⼥⽣?
(2)男⽣、⼥⽣身⾼数据集的正态分布的参数分别是多少?
具体问题如下图:
对于具体的身⾼问题使⽤EM算法求解步骤如下:
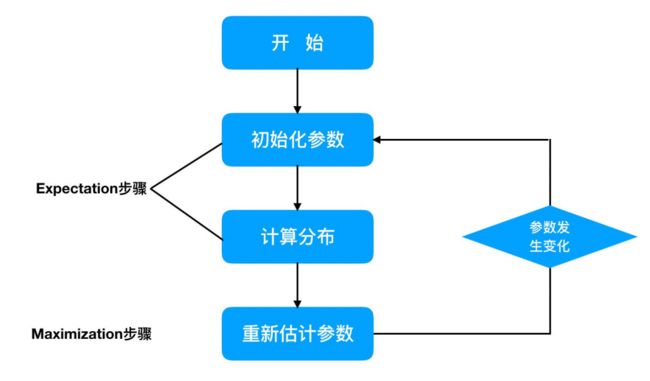
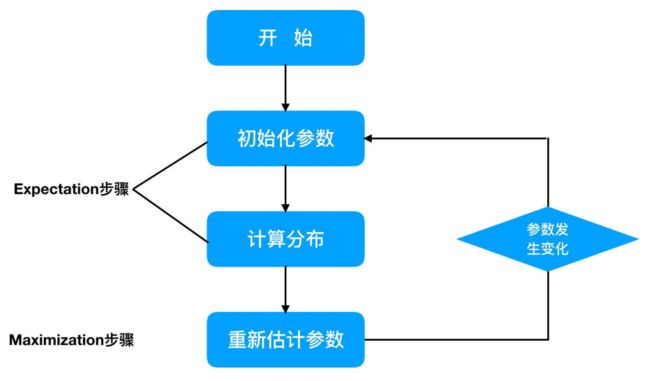
(1)初始化参数:先初始化男⽣身⾼的正态分布的参数:如均值=1.65,⽅差=0.15;
(2)计算分布:计算每⼀个⼈更可能属于男⽣分布或者⼥⽣分布;
(3)重新估计参数:通过分为男⽣的n个⼈来重新估计男⽣身⾼分布的参数(最⼤似然估计),⼥⽣分布也按照相同的⽅式估计出来,更新分布。
(4)这时候两个分布的概率也变了,然后重复步骤(1)⾄(3),直到参数不发⽣变化为⽌。
2.3 EM算法流程
输入:
- n个样本观察数据 x = ( x 1 , x 2 , . . . x n ) x=(x_1,x_2,...x_n) x=(x1,x2,...xn),未观察到的隐含数据 z = ( z 1 , z 2 , . . . , z n ) z=(z_1,z_2,...,z_n) z=(z1,z2,...,zn)
- 联合分布 p ( x , z ; θ ) p(x,z;\theta) p(x,z;θ),条件分布 p ( z ∣ x ; θ ) p(z|x;\theta) p(z∣x;θ),最大迭代次数 J J J
算法步骤:
1)随机初始化模型参数 θ \theta θ的初始值 θ 0 \theta_0 θ0
2)从 j = 1 , 2 , . . . J j=1,2,...J j=1,2,...J开始EM算法迭代:
-
E步:计算联合分布的条件概率期望:
Q i ( z i ) = p ( z i ∣ x i , θ j ) l ( θ , θ j ) = ∑ i = 1 n ∑ z i Q i ( z i ) l o g P ( x i , z i ; θ ) Q i ( z i ) Q_i(z_i)=p(z_i|x_i,\theta_j)\\ l(\theta,\theta_j)=\sum\limits_{i=1}^n \sum\limits_{z_i} Q_i(z_i)log \frac{P(x_i,z_i;\theta)}{Q_i(z_i)} Qi(zi)=p(zi∣xi,θj)l(θ,θj)=i=1∑nzi∑Qi(zi)logQi(zi)P(xi,zi;θ) -
M步:极大化 l ( θ , θ j ) l(\theta,\theta_j) l(θ,θj)得到 θ j + 1 \theta_{j+1} θj+1
θ j + 1 = a r g m a x l ( θ , θ j + 1 ) \theta_{j+1}=arg \ maxl(\theta,\theta_{j+1}) θj+1=arg maxl(θ,θj+1) -
如果 θ j + 1 \theta_{j+1} θj+1已经收敛,则算法结束,否则继续进行E步和M步进行迭代
-
输出:模型参数 θ \theta θ
3 EM算法实例
3.1 一个简单案例
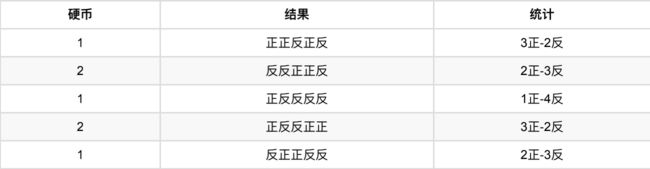
假设现在有两枚硬币1和2,它们随机抛掷后正⾯朝上的概率分别为P1,P2。为了估计这两个概率,我们做实验,每次取⼀枚硬币,连掷5下,记录下结果,如下:
可以很容易地估计出P1和P2,如下:
-
P 1 = 3 + 1 + 2 15 = 0.4 P1 = \frac{3+1+2}{15} = 0.4 P1=153+1+2=0.4
-
P 2 = 2 + 3 10 = 0.5 P2= \frac{2+3}{10}= 0.5 P2=102+3=0.5
到这⾥,⼀切似乎很美好,下⾯我们加⼤难度。
3.2 加入隐变量z后的求解
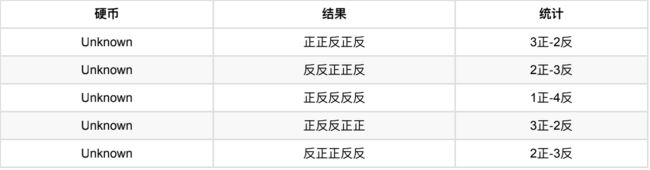
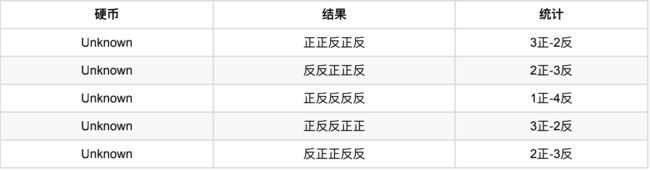
还是上⾯的问题,现在我们抹去每轮投掷时使⽤的硬币标记,如下:
好了,现在我们的⽬标没变,还是估计P1和P2,要怎么做呢?
显然,此时我们多了⼀个隐变量z,可以把它认为是⼀个5维的向量(z1,z2,z3,z4,z5),代表每次投掷时所使⽤的硬币,⽐如z1,就代表第⼀轮投掷时使⽤的硬币是1还是2。但是,这个变量z不知道,就⽆法去估计P1和P2,所以,我们必须先估计出z,然后才能进⼀步估计P1和P2。
但要估计z,我们⼜得知道P1和P2,这样我们才能⽤最⼤似然概率法则去估计z,这不是鸡⽣蛋和蛋⽣鸡的问题吗,如何破?
答案就是先随机初始化⼀个P1和P2,⽤它来估计z,然后基于z,还是按照最⼤似然概率法则去估计新的P1和P2,如果新的P1和P2和我们初始化的P1和P2⼀样,请问这说明了什么?(此处思考1分钟)
这说明我们初始化的P1和P2是⼀个相当靠谱的估计!
就是说,我们初始化的P1和P2,按照最⼤似然概率就可以估计出z,然后基于z,按照最⼤似然概率可以反过来估计出P1和P2,当与我们初始化的P1和P2⼀样时,说明是P1和P2很有可能就是真实的值。这⾥⾯包含了两个交互的最⼤似然估计。
如果新估计出来的P1和P2和我们初始化的值差别很⼤,怎么办呢?就是继续⽤新的P1和P2迭代,直⾄收敛。
这就是下⾯的EM初级版。
3.3 EM初级版
我们不妨这样,先随便给P1和P2赋⼀个值,⽐如:
-
P1 = 0.2
-
P2 = 0.7
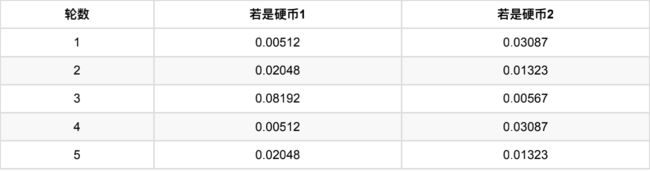
然后,我们看看第⼀轮抛掷最可能是哪个硬币。
-
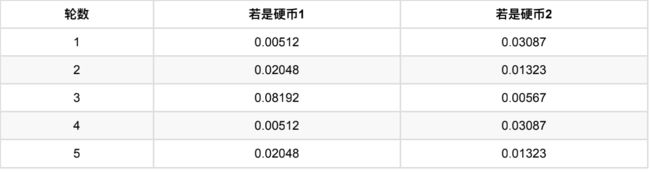
如果是硬币1,得出3正2反的概率为 0.2 ∗ 0.2 ∗ 0.2 ∗ 0.8 ∗ 0.8 = 0.00512 0.2 ∗ 0.2 ∗ 0.2 ∗ 0.8 ∗ 0.8 = 0.00512 0.2∗0.2∗0.2∗0.8∗0.8=0.00512
-
如果是硬币2,得出3正2反的概率为 0.7 ∗ 0.7 ∗ 0.7 ∗ 0.3 ∗ 0.3 = 0.03087 0.7 ∗ 0.7 ∗ 0.7 ∗ 0.3 ∗ 0.3 = 0.03087 0.7∗0.7∗0.7∗0.3∗0.3=0.03087
然后依次求出其他4轮中的相应概率。做成表格如下:
按照最⼤似然法则:
-
第1轮中最有可能的是硬币2
-
第2轮中最有可能的是硬币1
-
第3轮中最有可能的是硬币1
-
第4轮中最有可能的是硬币2
-
第5轮中最有可能的是硬币1
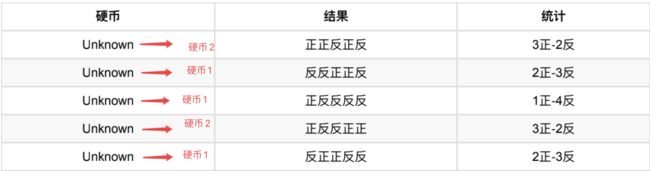
我们就把上⾯的值作为z的估计值。然后按照最⼤似然概率法则来估计新的P1和P2。
-
P 1 = 2 + 1 + 2 15 = 0.33 P1 = \frac{2+1+2}{15} = 0.33 P1=152+1+2=0.33
-
P 2 = 3 + 3 10 = 0.6 P2=\frac{3+3}{10} = 0.6 P2=103+3=0.6
设想我们是全知的神,知道每轮抛掷时的硬币就是如本⽂简单例子中图片的那样,那么,P1和P2的最⼤似然估计就是0.4和0.5(下⽂中将这两个值称为P1和P2的真实值)。那么对⽐下我们初始化的P1和P2和新估计出的P1和P2:
看到没?我们估计的P1和P2相⽐于它们的初始值,更接近它们的真实值了!
可以期待,我们继续按照上⾯的思路,⽤估计出的P1和P2再来估计z,再⽤z来估计新的P1和P2,反复迭代下去,就可以最终得到P1 = 0.4,P2=0.5,此时⽆论怎样迭代,P1和P2的值都会保持0.4和0.5不变,于是乎,我们就找到了P1和P2的最⼤似然估计。
这⾥有两个问题:
1、新估计出的P1和P2⼀定会更接近真实的P1和P2?
答案是:没错,⼀定会更接近真实的P1和P2,数学可以证明,但这超出了本⽂的主题,请参阅其他书籍或⽂章。
2、迭代⼀定会收敛到真实的P1和P2吗?
答案是:不⼀定,取决于P1和P2的初始化值,上⾯我们之所以能收敛到P1和P2,是因为我们幸运地找到了好的初始化值。
3.4 EM进阶版
下⾯,我们思考下,上⾯的⽅法还有没有改进的余地?
我们是⽤最⼤似然概率法则估计出的z值,然后再⽤z值按照最⼤似然概率法则估计新的P1和P2。也就是说,我们使⽤了⼀个最可能的z值,⽽不是所有可能的z值。
如果考虑所有可能的z值,对每⼀个z值都估计出⼀个新的P1和P2,将每⼀个z值概率⼤⼩作为权重,将所有新的P1和P2分别加权相加,这样的P1和P2应该会更好⼀些。
所有的z值有多少个呢?
- 显然,有 2 5 = 32 2^5 = 32 25=32种,难道需要我们进⾏32次估值吗?
不需要,我们可以⽤期望来简化运算。
利⽤上⾯这个表,我们可以算出每轮抛掷中使⽤硬币1或者使⽤硬币2的概率。
⽐如第1轮,使⽤硬币1的概率是: $\frac{0.00512}{0.00512 + 0.03087}= 0.14 $,使⽤硬币2的概率是$1-0.14=0.86 $
依次可以算出其他4轮的概率,如下:
| 轮数 | z i = 硬 币 1 z_i=硬币1 zi=硬币1 | z i = 硬 币 2 z_i=硬币2 zi=硬币2 |
|---|---|---|
| 1 | 0.14 | 0.86 |
| 2 | 0.61 | 0.39 |
| 3 | 0.94 | 0.06 |
| 4 | 0.14 | 0.86 |
| 5 | 0.61 | 0.39 |
上表中的右两列表示期望值。看第⼀⾏,0.86表示,从期望的⻆度看,**这轮抛掷使⽤硬币2的概率是0.86。相⽐于前⾯的⽅法,我们按照最⼤似然概率,直接将第1轮估计为⽤的硬币2,此时的我们更加谨慎,我们只说,有0.14的概率是硬币1,有0.86的概率是硬币2,不再是⾮此即彼。**这样我们在估计P1或者P2时,就可以⽤上全部的数据,⽽不是部分的数据,显然这样会更好⼀些。
这⼀步,我们实际上是估计出了z的概率分布,这步被称作E步。
结合下表:
我们按照期望最⼤似然概率的法则来估计新的P1和P2:
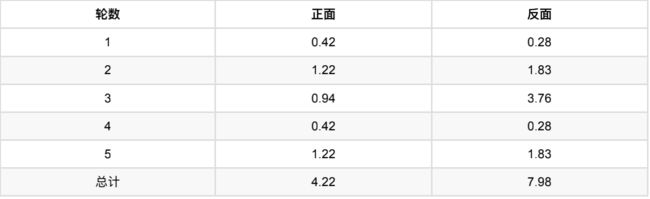
以P1估计为例,第1轮的3正2反相当于
-
0.14*3=0.42正
-
0.14*2=0.28反
第二轮的2正3反:
- 0.61*2=1.22正
- 0.61*3=1.83反
依次算出其他四轮,列表如下:
此时, P 1 = 4.22 4.22 + 7.98 = 0.35 P1=\frac{4.22}{4.22+7.98}=0.35 P1=4.22+7.984.22=0.35
可以看到,改变了z值的估计⽅法后,新估计出的P1要更加接近0.4。原因就是我们使⽤了所有抛掷的数据,⽽不是之前只使⽤了部分的数据。
这步中,我们根据E步中求出的z的概率分布,依据最⼤似然概率法则去估计P1和P2,被称作M步。