机器学习KNN-应用:手写数字识别(手撕+sklearn实现)
目录
-
- 导入数据集
- 划分数据集
- 使用sklearn库中的KNN 模型解决问题
- K折交叉验证:模型稳定性
- 归一化
- 使用自己写的KNN模型解决问题
- 补充:(from cs231n)
参考链接
导入数据集
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 数据集的导入
from sklearn.datasets import load_digits
load_digits()
{'data': array([[ 0., 0., 5., ..., 0., 0., 0.],
[ 0., 0., 0., ..., 10., 0., 0.],
[ 0., 0., 0., ..., 16., 9., 0.],
...,
[ 0., 0., 1., ..., 6., 0., 0.],
[ 0., 0., 2., ..., 12., 0., 0.],
[ 0., 0., 10., ..., 12., 1., 0.]]),
'target': array([0, 1, 2, ..., 8, 9, 8]),
'frame': None,
'feature_names': ['pixel_0_0',
'pixel_0_1',
'pixel_0_2',
'pixel_0_3',
'pixel_0_4',
'pixel_0_5',
'pixel_0_6',
'pixel_0_7',
'pixel_1_0',
'pixel_1_1',
'pixel_1_2',
'pixel_1_3',
'pixel_1_4',
'pixel_1_5',
'pixel_1_6',
'pixel_1_7',
'pixel_2_0',
'pixel_2_1',
'pixel_2_2',
'pixel_2_3',
'pixel_2_4',
'pixel_2_5',
'pixel_2_6',
'pixel_2_7',
'pixel_3_0',
'pixel_3_1',
'pixel_3_2',
'pixel_3_3',
'pixel_3_4',
'pixel_3_5',
'pixel_3_6',
'pixel_3_7',
'pixel_4_0',
'pixel_4_1',
'pixel_4_2',
'pixel_4_3',
'pixel_4_4',
'pixel_4_5',
'pixel_4_6',
'pixel_4_7',
'pixel_5_0',
'pixel_5_1',
'pixel_5_2',
'pixel_5_3',
'pixel_5_4',
'pixel_5_5',
'pixel_5_6',
'pixel_5_7',
'pixel_6_0',
'pixel_6_1',
'pixel_6_2',
'pixel_6_3',
'pixel_6_4',
'pixel_6_5',
'pixel_6_6',
'pixel_6_7',
'pixel_7_0',
'pixel_7_1',
'pixel_7_2',
'pixel_7_3',
'pixel_7_4',
'pixel_7_5',
'pixel_7_6',
'pixel_7_7'],
'target_names': array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]),
'images': array([[[ 0., 0., 5., ..., 1., 0., 0.],
[ 0., 0., 13., ..., 15., 5., 0.],
[ 0., 3., 15., ..., 11., 8., 0.],
...,
[ 0., 4., 11., ..., 12., 7., 0.],
[ 0., 2., 14., ..., 12., 0., 0.],
[ 0., 0., 6., ..., 0., 0., 0.]],
[[ 0., 0., 0., ..., 5., 0., 0.],
[ 0., 0., 0., ..., 9., 0., 0.],
[ 0., 0., 3., ..., 6., 0., 0.],
...,
[ 0., 0., 1., ..., 6., 0., 0.],
[ 0., 0., 1., ..., 6., 0., 0.],
[ 0., 0., 0., ..., 10., 0., 0.]],
[[ 0., 0., 0., ..., 12., 0., 0.],
[ 0., 0., 3., ..., 14., 0., 0.],
[ 0., 0., 8., ..., 16., 0., 0.],
...,
[ 0., 9., 16., ..., 0., 0., 0.],
[ 0., 3., 13., ..., 11., 5., 0.],
[ 0., 0., 0., ..., 16., 9., 0.]],
...,
[[ 0., 0., 1., ..., 1., 0., 0.],
[ 0., 0., 13., ..., 2., 1., 0.],
[ 0., 0., 16., ..., 16., 5., 0.],
...,
[ 0., 0., 16., ..., 15., 0., 0.],
[ 0., 0., 15., ..., 16., 0., 0.],
[ 0., 0., 2., ..., 6., 0., 0.]],
[[ 0., 0., 2., ..., 0., 0., 0.],
[ 0., 0., 14., ..., 15., 1., 0.],
[ 0., 4., 16., ..., 16., 7., 0.],
...,
[ 0., 0., 0., ..., 16., 2., 0.],
[ 0., 0., 4., ..., 16., 2., 0.],
[ 0., 0., 5., ..., 12., 0., 0.]],
[[ 0., 0., 10., ..., 1., 0., 0.],
[ 0., 2., 16., ..., 1., 0., 0.],
[ 0., 0., 15., ..., 15., 0., 0.],
...,
[ 0., 4., 16., ..., 16., 6., 0.],
[ 0., 8., 16., ..., 16., 8., 0.],
[ 0., 1., 8., ..., 12., 1., 0.]]]),
'DESCR': ".. _digits_dataset:\n\nOptical recognition of handwritten digits dataset\n--------------------------------------------------\n\n**Data Set Characteristics:**\n\n :Number of Instances: 1797\n :Number of Attributes: 64\n :Attribute Information: 8x8 image of integer pixels in the range 0..16.\n :Missing Attribute Values: None\n :Creator: E. Alpaydin (alpaydin '@' boun.edu.tr)\n :Date: July; 1998\n\nThis is a copy of the test set of the UCI ML hand-written digits datasets\nhttps://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits\n\nThe data set contains images of hand-written digits: 10 classes where\neach class refers to a digit.\n\nPreprocessing programs made available by NIST were used to extract\nnormalized bitmaps of handwritten digits from a preprinted form. From a\ntotal of 43 people, 30 contributed to the training set and different 13\nto the test set. 32x32 bitmaps are divided into nonoverlapping blocks of\n4x4 and the number of on pixels are counted in each block. This generates\nan input matrix of 8x8 where each element is an integer in the range\n0..16. This reduces dimensionality and gives invariance to small\ndistortions.\n\nFor info on NIST preprocessing routines, see M. D. Garris, J. L. Blue, G.\nT. Candela, D. L. Dimmick, J. Geist, P. J. Grother, S. A. Janet, and C.\nL. Wilson, NIST Form-Based Handprint Recognition System, NISTIR 5469,\n1994.\n\n.. topic:: References\n\n - C. Kaynak (1995) Methods of Combining Multiple Classifiers and Their\n Applications to Handwritten Digit Recognition, MSc Thesis, Institute of\n Graduate Studies in Science and Engineering, Bogazici University.\n - E. Alpaydin, C. Kaynak (1998) Cascading Classifiers, Kybernetika.\n - Ken Tang and Ponnuthurai N. Suganthan and Xi Yao and A. Kai Qin.\n Linear dimensionalityreduction using relevance weighted LDA. School of\n Electrical and Electronic Engineering Nanyang Technological University.\n 2005.\n - Claudio Gentile. A New Approximate Maximal Margin Classification\n Algorithm. NIPS. 2000.\n"}
X = load_digits().data
y = load_digits().target
pics = load_digits().images
X[0].shape
(64,)
y.shape
(1797,)
pd.Series(y).value_counts()
3 183
5 182
1 182
6 181
4 181
9 180
7 179
0 178
2 177
8 174
dtype: int64
pics[7]
array([[ 0., 0., 7., 8., 13., 16., 15., 1.],
[ 0., 0., 7., 7., 4., 11., 12., 0.],
[ 0., 0., 0., 0., 8., 13., 1., 0.],
[ 0., 4., 8., 8., 15., 15., 6., 0.],
[ 0., 2., 11., 15., 15., 4., 0., 0.],
[ 0., 0., 0., 16., 5., 0., 0., 0.],
[ 0., 0., 9., 15., 1., 0., 0., 0.],
[ 0., 0., 13., 5., 0., 0., 0., 0.]])
X[7]
array([ 0., 0., 7., 8., 13., 16., 15., 1., 0., 0., 7., 7., 4.,
11., 12., 0., 0., 0., 0., 0., 8., 13., 1., 0., 0., 4.,
8., 8., 15., 15., 6., 0., 0., 2., 11., 15., 15., 4., 0.,
0., 0., 0., 0., 16., 5., 0., 0., 0., 0., 0., 9., 15.,
1., 0., 0., 0., 0., 0., 13., 5., 0., 0., 0., 0.])
plt.imshow(pics[7],cmap='gray')
y[7]
7
划分数据集
# 划分数据集
from sklearn.model_selection import train_test_split
xtrain,xtest,ytrain,ytest = train_test_split(X,y,random_state=5)
xtrain.shape,ytrain.shape,xtest.shape,ytest.shape
((1347, 64), (1347,), (450, 64), (450,))
使用sklearn库中的KNN 模型解决问题
# 使用sklearn库中的KNN 模型解决问题
from sklearn.neighbors import KNeighborsClassifier
knn1 = KNeighborsClassifier(n_neighbors=5).fit(xtrain,ytrain)
%%time
# 预测
res = knn1.predict(xtest)
res
Wall time: 82 ms
array([5, 2, 5, 5, 5, 3, 2, 2, 3, 5, 9, 8, 7, 7, 1, 1, 5, 7, 0, 4, 5, 9,
0, 2, 1, 3, 4, 7, 5, 2, 1, 1, 2, 9, 8, 1, 4, 5, 7, 9, 5, 5, 6, 0,
1, 7, 2, 9, 7, 7, 3, 9, 5, 1, 8, 6, 7, 7, 8, 1, 6, 1, 3, 6, 1, 3,
2, 6, 8, 1, 4, 7, 1, 6, 0, 0, 5, 1, 3, 5, 1, 6, 4, 0, 4, 7, 5, 7,
8, 3, 7, 8, 5, 1, 1, 7, 5, 9, 7, 9, 3, 0, 7, 8, 7, 4, 8, 3, 2, 8,
5, 2, 7, 4, 4, 8, 9, 7, 4, 5, 0, 5, 9, 8, 2, 3, 2, 4, 4, 8, 0, 5,
2, 9, 4, 8, 6, 5, 9, 9, 8, 0, 9, 4, 3, 8, 7, 5, 5, 3, 3, 5, 1, 0,
8, 7, 2, 8, 4, 1, 0, 0, 3, 6, 4, 7, 7, 0, 4, 9, 2, 8, 7, 9, 7, 2,
0, 3, 3, 8, 5, 7, 5, 6, 8, 4, 1, 5, 1, 1, 6, 9, 9, 9, 8, 6, 4, 6,
0, 1, 6, 5, 3, 5, 0, 2, 7, 8, 8, 7, 3, 8, 3, 9, 3, 0, 9, 6, 0, 4,
0, 3, 5, 0, 4, 3, 5, 8, 8, 9, 2, 5, 0, 8, 3, 7, 4, 3, 7, 9, 2, 6,
1, 2, 1, 7, 0, 7, 5, 0, 6, 4, 1, 8, 3, 0, 8, 9, 2, 2, 5, 2, 6, 6,
3, 4, 0, 7, 1, 5, 3, 8, 7, 3, 4, 2, 5, 1, 3, 0, 0, 9, 3, 8, 8, 3,
5, 8, 6, 6, 2, 6, 7, 5, 3, 1, 5, 7, 5, 4, 5, 2, 6, 2, 0, 6, 0, 7,
2, 5, 8, 8, 7, 1, 4, 7, 2, 0, 0, 3, 7, 4, 2, 5, 2, 6, 1, 0, 5, 7,
2, 9, 1, 6, 9, 6, 5, 4, 8, 8, 0, 9, 3, 5, 7, 1, 2, 4, 1, 6, 6, 2,
1, 5, 8, 0, 3, 2, 4, 3, 9, 0, 0, 3, 2, 8, 9, 0, 2, 5, 2, 2, 5, 8,
3, 6, 7, 2, 5, 9, 0, 5, 9, 0, 1, 3, 9, 1, 4, 9, 2, 1, 5, 6, 0, 0,
9, 6, 7, 9, 9, 3, 1, 4, 3, 4, 7, 2, 5, 2, 6, 0, 3, 4, 9, 3, 1, 0,
3, 7, 6, 0, 7, 1, 0, 5, 1, 3, 5, 7, 7, 0, 1, 1, 5, 1, 1, 1, 6, 7,
7, 2, 2, 2, 7, 1, 3, 6, 9, 1])
(ytest == res).mean()
0.9822222222222222
knn1.score(xtest,ytest)
0.9822222222222222
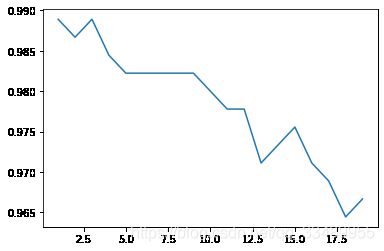
# 学习曲线
def learning_curve():
krange = range(1,20)
score = []
for i in krange:
clf = KNeighborsClassifier(n_neighbors = i)
clf = clf.fit(xtrain,ytrain)
score.append(clf.score(xtest,ytest))
print(score.index(max(score))+1) # 打印最佳k值
plt.plot(krange,score)
plt.show()
learning_curve()
1
knn1_1 = KNeighborsClassifier(n_neighbors = 3).fit(xtrain,ytrain)
knn1_1.score(xtest,ytest)
0.9888888888888889
# 此时的k只是在某一特定数据集下的最优,随着测试集的变动,最优的k也会变,所以需要寻找更加稳定最优k:交叉验证法
K折交叉验证:模型稳定性
# K折交叉验证:模型稳定性
from sklearn.model_selection import cross_val_score as CVS
def cross_validation():
clf = KNeighborsClassifier(n_neighbors = 3)
cvresult = CVS(clf,X,y,cv=10) # cv折数
c_mean = cvresult.mean()
c_std = cvresult.std()
print('cvresult:',cvresult,'cvresult.mean():',c_mean,'cvresult.std():',c_std)
# 绘制K折交叉验证曲线
score = []
var_ = []
krange = range(1,20)
for i in krange:
clf = KNeighborsClassifier(n_neighbors = i)
cvresult = CVS(clf,xtrain,ytrain,cv = 5)
score.append(cvresult.mean())
var_.append(cvresult.var())
best_k = score.index(max(score))+1
print('best_k:',best_k)
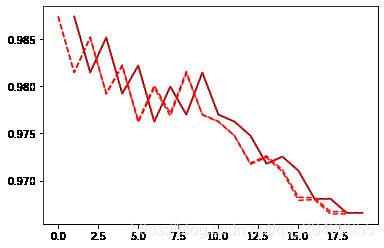
plt.plot(krange,score,color = 'k')
plt.plot(krange,score,np.array(score)+np.array(var_)*2,c='red',linestyle = '--')
plt.plot(krange,score,np.array(score)-np.array(var_)*2,c='red',linestyle = '--')
cross_validation()
cvresult: [0.93888889 1. 0.98888889 0.97222222 0.96666667 0.97777778
0.98333333 0.98324022 0.98324022 0.97206704] cvresult.mean(): 0.9766325263811299 cvresult.std(): 0.015472517471692416
best_k: 1
归一化
# 归一化
x_train = xtrain/255
x_test = xtest/255
score=[]
var_=[]
krange = range(1,20)
for i in krange:
clf=KNeighborsClassifier(n_neighbors=i,weights = 'distance')
cvresult = CVS(clf,x_train,ytrain,cv=5)
score.append(cvresult.mean())
var_.append(cvresult.var())
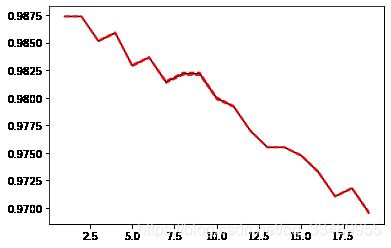
plt.plot(krange,score,color='k')
plt.plot(krange,np.array(score)+np.array(var_)*2,c='red',linestyle='--')
plt.plot(krange,np.array(score)-np.array(var_)*2,c='red',linestyle='--')
[]
# 归一化后返回最优的k
best_index = krange[score.index(max(score))]-1
print('best_index',best_index)
print(score[best_index])
best_index 0
0.9873798705768966
使用自己写的KNN模型解决问题
# 使用自己写的KNN模型解决问题
def Knn_C(X,y,X_sample,k):
d = np.sqrt(np.sum((X-X_sample)**2,axis = 1))
knn = [*zip(d,y)]
knn.sort()
# 少数服从多数,X1的类型与最多的邻居的类型一致,取排序后的前k个值,的第二列(标签值),取第一个众数作为测试数据的预测值
Y_sample = pd.Series(np.array(knn[:k])[:,1]).mode()[0]
return Y_sample
def handwtitingClassTest():
errorCount = 0.0
lenth = float(*y.shape)
for i,item in enumerate(X):
# 预测
classifierResult = Knn_C(X,y,item,3)
# 打印结果
print(f'测试样本编号:{i},分类器预测结果:{classifierResult},真实结果:{y[i]}')
# 判断结果是否正确
if(classifierResult!=y[i]):
errorCount +=1.0
# print(y.shape)#(1797,)
# 打印错误率
print(f'错误率:{errorCount/lenth},正确率:{1-errorCount/lenth}')
handwtitingClassTest()
补充:(from cs231n)
视频中给出的knn代码实现

在调整超参数的时候,你不能只选择对于整个数据集有最好效果的那个参数,对于knn来说就是k=1时准确率高,但是不具备泛化性。
在调整超参数的时候,你同样不能选择在测试集上效果最好的超参数,因为这个超参数只对这个测试集有泛化性,想要得到比较准确的结果,可以进行k折交叉验证得到一个均值作为最终结果。
此外,为了避免第二种情况的发生,可以设置验证集,测试集在最终结果(确定好超参数)出来前不参与预测,保证研究的可靠性。