CS224W-08-Graph Neural Networks
Graph Neural Network
本文为中文笔记翻译,其英文原文地址为Graph Neural Network
在上一节中,我们学习了如何使用“浅层编码器”表示图。这些技术为我们提供了在向量空间中表示图的强大方式,但也有其局限性。在本节中,我们将探索使用图神经网络克服限制的三种不同方法。
Limitation of “Shallow Encoders”(浅层编码器”的局限性)
- 浅编码器无法缩放,因为每个节点都有唯一的嵌入。
- 浅层编码器具有固有的传导性。它只能为单个固定图生成嵌入。
- 不考虑节点的特征。
- 不能将浅层编码器推广到具有不同损失函数的训练中。
幸运的是,图神经网络可以解决上述限制。
Graph convolutional Networks(GCN, 图神经网络)
传统上,神经网络是为固定大小的图设计的。例如,我们可以将图像视为网格图,或将一段文本视为线图。但是,现实世界中的大多数图具有任意大小和复杂的拓扑结构。因此,我们需要不同地定义GCN的计算图。
假设给定图 G = ( V , A , X ) G=(V,A,X) G=(V,A,X) :
- V V V 是顶点集合
- A A A 是邻接矩阵
- X ∈ R m × ∣ V ∣ X \in \mathbb{R}^{m \times|V|} X∈Rm×∣V∣ 是节点的特征矩阵
计算图和广义卷积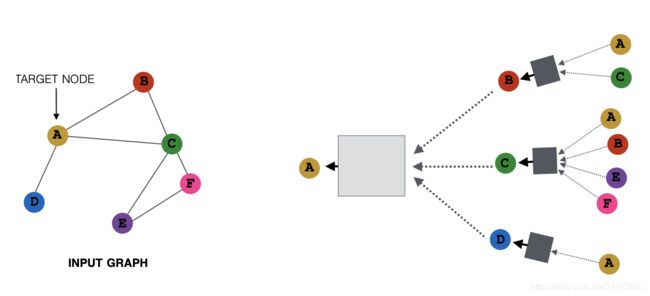
假设示例图(上图左图)为图 G G G 。我们的目标是定义在图 G G G 上的GCN计算图。计算图应同时保持图 G G G 的结构和合并节点的相邻要素。例如,节点的嵌入向量 A A A 应该包括它的邻居 { B , C , D } \left\{B,C,D\right\} {B,C,D} 并且和 { B , C , D } \left\{B,C,D\right\} {B,C,D} 的顺序无关。一种方法是简单地取 { B , C , D } \left\{B,C,D\right\} {B,C,D} 的平均值。通常,聚合函数(上图右图中的方框)必须是阶不变的(最大值,平均值等)。上图具有两层计算图 G G G 如下所示:
这里,每个节点都基于其邻居定义一个计算图。特别的,节点 A A A 的计算图结构如下所示:(第0层是输入层,输入为节点特征 X i X_{i} Xi ):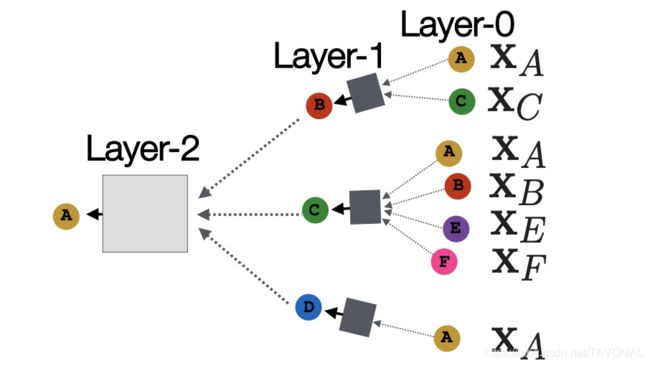
Deep Encoders(深度编码器)
有了以上想法,这是节点 v v v 使用平均聚合函数的每一层的数学表达式 :
- 在第0层: h v 0 = x v h_{v}^{0} = x_{v} hv0=xv, 表示节点特征
- 在第k层:
h v k = σ ( W k ∑ u ∈ N ( v ) h u k − 1 ∣ N ( v ) ∣ + B k h v k − 1 ) , ∀ k ∈ { 1 , … , K } h_{v}^{k}=\sigma\left(W_{k} \sum_{u \in N(v)} \frac{h_{u}^{k-1}}{|N(v)|}+B_{k} h_{v}^{k-1}\right), \forall k \in\{1, \ldots, K\} hvk=σ(Wk∑u∈N(v)∣N(v)∣huk−1+Bkhvk−1),∀k∈{1,…,K}
h v k − 1 h_{v}^{k-1} hvk−1 是节点 v v v 从上一层开始的嵌入。 ∣ N ( v ) ∣ |N(v)| ∣N(v)∣ 是节点 v v v 的邻居数。$\sum_{u \in N(v)}\frac{h_{u}^{k-1}}{|N(v)|} $ 的目的是聚合节点 v v v 上一层的所有邻居特征。 σ \sigma σ 是引入非线性的激活函数(例如ReLU)。 W k W_{k} Wk 和 B k B_{k} Bk 是可训练的参数。
- 输出层: z v = h v K z_{v}=h_{v}^K zv=hvK 是K层嵌入后的最后的嵌入层。
等效地,以上计算可以以写成整个图矩阵乘法的形式:
H l + 1 = σ ( H l W 0 l + A ~ H l W 1 l ) such that A ~ = D − 1 2 A D − 1 2 H^{l+1}=\sigma\left(H^{l} W_{0}^{l}+\tilde{A} H^{l} W_{1}^{l}\right) \text { such that } \tilde{A}=D^{-\frac{1}{2}} A D^{-\frac{1}{2}} Hl+1=σ(HlW0l+A~HlW1l) such that A~=D−21AD−21
Training the Model
我们可以为这些嵌入提供给任何损失函数,并进行随机梯度下降训练参数。例如,对于二进制分类任务,我们可以将损失函数定义为:
L = ∑ v ∈ V y v log ( σ ( z v T θ ) ) + ( 1 − y v ) log ( 1 − σ ( z v T θ ) ) L=\sum_{v \in V} y_{v} \log \left(\sigma\left(z_{v}^{T} \theta\right)\right)+\left(1-y_{v}\right) \log \left(1-\sigma\left(z_{v}^{T} \theta\right)\right) L=v∈V∑yvlog(σ(zvTθ))+(1−yv)log(1−σ(zvTθ))
y v ∈ { 0 , 1 } y_{v}\in\left\{0,1\right\} yv∈{0,1} 是节点类标签。 z v z_{v} zv 是编码器的输出。$\theta $ 是分类权重。 σ \sigma σ 可以是 sigmoid 函数。 σ ( z v T θ ) \sigma(z^T_{v}\theta) σ(zvTθ) 表示节点 v v v 的预测概率。因此,如果标签为正 ( y v = 1 ) (y_{v}=1) (yv=1),则损失函数方程将计算前半部分,否则,损失函数方程将计算后半部分。
我们还可以通过以下方式以无监督的方式训练模型:随机游走,图形分解,节点接近等。
Inductive Capability(归纳能力)
GCN可以应用在图中看不见的节点。例如,如果使用节点 A , B , C A,B,C A,B,C 训练模型,由于参数在所有节点之间共享,新添加的节点 D , E , F D,E,F D,E,F 因此也可以进行评估。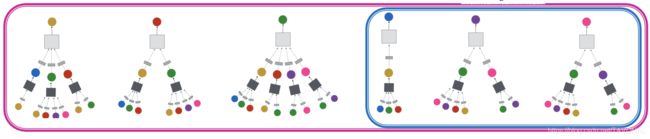
GraphSAGE
本文为中文笔记翻译,其英文原文地址为Graph Neural Networks
到目前为止,我们已经探索了一种简单的邻域聚合方法,但是我们还可以将聚合方法概括为以下形式:
h v K = σ ( [ W k A G G ( { h u k − 1 , ∀ u ∈ N ( v ) } ) , B k h v k − 1 ] ) h_{v}^{K}=\sigma\left(\left[W_{k} A G G\left(\left\{h_{u}^{k-1}, \forall u \in N(v)\right\}\right), B_{k} h_{v}^{k-1}\right]\right) hvK=σ([WkAGG({huk−1,∀u∈N(v)}),Bkhvk−1])
对于节点 v v v,我们可以应用不同的汇总方法( A G G AGG AGG)与将其邻居和节点 v v v 本身的特征相连接。
下面是一些常用的聚合函数:
-
平均值:取其邻居的加权平均值。
A G G = ∑ u ∈ N v h u k − 1 ∣ N ( v ) ∣ AGG=\sum_{u\in N_{v}}\frac{h_{u}^{k-1}}{|N(v)|} AGG=u∈Nv∑∣N(v)∣huk−1 -
池化:转换邻居向量并应用对称向量函数( γ \gamma γ 可以是按元素的均值或最大值)。
A G G = γ ( { Q h u k − 1 , ∀ u ∈ N ( v ) } ) AGG=\gamma(\left\{Qh_{u}^{k-1},\forall u\in N(v)\right\}) AGG=γ({Qhuk−1,∀u∈N(v)}) -
LSTM:使用LSTM应用于重组后的邻居。
A G G = L S T M ( { h u k − 1 , ∀ u ∈ π ( N ( v ) ) } ) AGG=LSTM(\left\{h_{u}^{k-1},\forall u\in \pi (N(v))\right\}) AGG=LSTM({huk−1,∀u∈π(N(v))})
Graph Attention Networks(图注意力网络)
如果某些相邻节点携带的信息比其他节点更重要怎么办?在这种情况下,我们希望通过使用注意力技巧将不同的权重分配给不同的相邻节点。
假设 α v u \alpha_{vu} αvu 是节点 u u u 向节点 v v v 传递的信息的加权因子(重要性)。 根据上面的平均聚合函数,我们定义了 α = 1 ∣ N ( v ) ∣ \alpha=\frac{1}{|N(v)|} α=∣N(v)∣1。但是,我们也可以基于图的结构特性显式定义 α \alpha α。
Attention Mechanism(注意力机制)
设 α u v \alpha_{uv} αuv 为计算注意力机制 a a a 的副产物,它根据节点对 u , v u,v u,v 的消息计算注意力系数 e v u e_{vu} evu:
e v u = a ( W k h u k − 1 , W k h v k − 1 ) e_{vu}=a(W_{k}h_{u}^{k-1}, W_{k}h_{v}^{k-1}) evu=a(Wkhuk−1,Wkhvk−1)
e v u e_{vu} evu 表示了节点 u u u 向节点 v v v 传递的信息的重要性,然后,我们使用 softmax 函数归一化系数以比较不同邻居之间的重要性:
α = exp ( e v u ) ∑ k ∈ N ( v ) exp ( e v k ) \alpha=\frac{\exp(e_{vu})} {\sum_{k\in N(v) \exp (e_{v k})}} α=∑k∈N(v)exp(evk)exp(evu)
因此有:
h v k = σ ( ∑ u ∈ N ( v ) α v u W k h u k − 1 ) h_{v}^{k}=\sigma(\sum_{u \in N(v)}\alpha_{v u}W_{k}h_{u}^{k-1}) hvk=σ(u∈N(v)∑αvuWkhuk−1)
该方法与的选择的 a a a 无关,并且可以与 W k W_{k} Wk 一起训练参数。
参考
以下是有用的参考资料列表:
教程和概述:
- Relational inductive biases and graph networks (Battaglia et al., 2018)
- Representation learning on graphs: Methods and applications (Hamilton et al., 2017)
基于注意力的邻居节点聚合:
- Graph attention networks (Hoshen, 2017; Velickovic et al., 2018; Liu et al., 2018)
整个图嵌入:
- Graph neural nets with edge embeddings (Battaglia et al., 2016; Gilmer et. al., 2017)
- Embedding entire graphs (Duvenaud et al., 2015; Dai et al., 2016; Li et al., 2018) and graph pooling (Ying et al., 2018, Zhang et al., 2018)
- Graph generation and relational inference (You et al., 2018; Kipf et al., 2018)
- How powerful are graph neural networks(Xu et al., 2017)
节点嵌入:
- Varying neighborhood: Jumping knowledge networks Xu et al., 2018), GeniePath (Liu et al., 2018
- Position-aware GNN (You et al. 2019)
图神经网络的谱方法:
- Spectral graph CNN & ChebNet [Bruna et al., 2015; Defferrard et al., 2016)
- Geometric deep learning (Bronstein et al., 2017; Monti et al., 2017)
其他GNN方法
- Pre-training Graph Neural Networks (Hu et al., 2019)
- GNNExplainer: Generating Explanations for Graph Neural Networks (Ying et al., 2019)