【多目标追踪算法】Deepsort算法核心---卡尔曼滤波与匈牙利算法

参考博客：

目标追踪—deepsort原理讲解

目标追踪中的核心算法:卡尔曼滤波&匈牙利算法详解与实战

Deepsort的前身是sort算法，sort算法的核心是 卡尔曼滤波算法和匈牙利算法。
下面简单分析这两种算法。

一、卡尔曼滤波算法

之前在嵌入式平台stm32中也用到过kalman滤波：一阶卡尔曼滤波原理和ADC读取红外测距模块的数值。

那么kalman滤波在追踪中又是怎样起作用的呢？

在大三学完现代控制系统后，更深一步体会到了：卡尔曼滤波器主要用于对实际系统状态的估计上。 本质上来说，卡尔曼滤波器就不是一个滤波器，而是一个算法。（最优化递归数字处理算法）其算法思想是：估计值 = 预测+更新

1. 物理举例

学过现代控制系统很好理解下面的式子。所谓矩阵表达式就是 状态空间表达式 嘛。

选取的状态向量是位置 Xt 和速度 X‘t。
得到状态空间表达式，Ft 矩阵为系统矩阵，Bt 矩阵为控制矩阵。

可以看到实际系统的输出状态不仅与上一时刻的状态相关，还和系统输入 uk 、与系统状态相互独立的高斯噪声 Wk 有关。

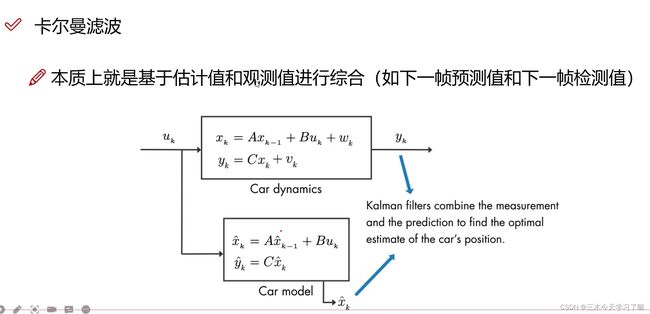
这是一个开环全维状态观测器。对照实际的物理模型，新建一个预测的模型，并对实际模型的输出与预测模型的预测输出做结合（权重不同）来实现一个最优的估计值。

回答一开始的问题：kalman滤波在追踪中又是怎样起作用的呢？

这个思想体现在目标追踪上就是：我们网络生成了t时刻帧的锚框，在 t+1 时刻又生成了一个帧的锚框。但同时也根据t时刻的锚框生成了t+1时刻的预测锚框。那么我们 t+1 时刻的实际锚框就是比较这两个锚框的 IOU，根据匈牙利算法来确定最终实际的框。

比如，我们在 k-1 时刻传感器检测的状态是最左边的正态分布估计值（带高斯噪声的检测值）。在 k 时刻有两个值，一个是传感器检测的状态；一个是根据上一时刻预测的状态值（方差会更大）。

最优估计值为测量值（高斯分布）与预测值（高斯分布）的乘积，乘积如下：

2. 核心公式

一阶卡尔曼滤波原理 之前做过了，不在这里赘述了。

二、匈牙利算法

匈牙利算法(Hungarian Algorithm)是一种组合优化算法(combinatorial optimization algorithm)，用于求解指派问题(assignment problem)。

带你入门多目标跟踪（三）匈牙利算法&KM算法

这篇博客介绍的实在是太详细了，不做多赘述。

匈牙利算法在追踪中又是怎样起作用的呢？

个人理解：在多目标跟踪中解决数据关联（检测框和预测框 与 实际框 的匹配）的问题。

三、sort算法

1. kalman滤波部分

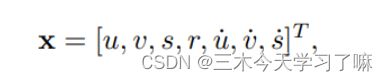
这里的状态变量有7个，分别为，检测框中心的横坐标，检测框中心的纵坐标，检测框的面积，长宽比，横坐标速度，纵坐标速度，面积速度。

将第一帧检测到的结果创建其对应的Tracks（轨迹信息）。将卡尔曼滤波的运动变量初始化，通过卡尔曼滤波预测下一帧的框。

2. 匈牙利算法部分

将该帧目标检测的框和上一帧通过卡尔曼滤波预测的框一一进行IOU匹配，再通过IOU匹配的结果计算其代价矩阵（cost matrix，其计算方式是1-IOU）。而代价矩阵作为匈牙利算法的输入，得到线性的匹配的结果。

这就造成了Sort算法注定无法解决两个行人重叠路过的问题！！所以其IDSW（ID switch）这个指标很差。【IDSW（ID switch），对于同一个目标，由于跟踪算法误判，导致其ID发生切换的次数称为IDSW。跟踪算法中理想的ID switch应该为0。】
且其直接丢弃掉IOU小于阈值的作法也导致了无法解决遮挡的问题。

四、deepsort算法

Deepsort算法在sort算法的基础上增加了 级联匹配（Matching Cascade） 和 新轨迹的确认（confirmed）。
Tracks分为确认态（confirmed）和不确认态（unconfirmed），新产生的Tracks是不确认态的；不确认态的Tracks必须要和Detections连续匹配一定的次数（默认是3）才可以转化成确认态。确认态的Tracks必须和Detections连续失配一定次数（默认30次），才会被删除。

1. kalman滤波部分

相对于Sort算法中7个维度的信息，Deepsort中使用了8个维度的信息，分别为目标框中心坐标（u，v），长宽比γ，高h以及这四个变量的一阶导数，表示变换速率。

2. 匈牙利算法部分

多目标跟踪（二）DeepSort——级联匹配Matching Cascade

在DeepSort中，由上面所说的，在非确定态下和Sort类似，都是以IOU为代价矩阵。

而在确定态下DeepSort引入了马氏距离和余弦距离。在DeepSort中马氏距离最终用于筛选掉不符合要求的框，而余弦距离才是作为真正的代价矩阵的计算。

DeepSort中，对于卡尔曼滤波的结果分为确定态和非确定态，对于确定态的预测结果，才会进行级联匹配。

2.1 马氏距离

一个可以描述两个向量之间距离的度量，其考虑了两者的“位置”相近程度、不确定性、相关性。

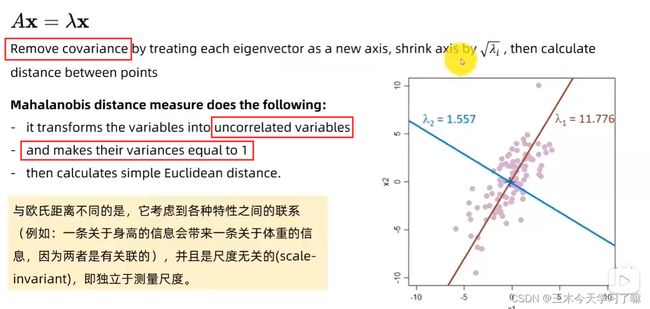
虽然黄点和蓝点到橙色点的欧氏距离相等，但明显可以看到黄点和数据关联度更大，这在马氏距离的计算中也得到了体现。

可以看到在双变量中，若两个正态分布的变量没有协方差且权重都是1，则是一个单位圆。若权重不同则是一个椭圆。若变量之间相关联，即有协方差，则是一个坐标轴旋转一定角度的椭圆。

这里我们简单的理解马氏距离在多目标追踪中作用：

剔除两个距离很远的框匹配成功的情况

看追踪和检测的Bbox的状态向量的前四维度 cx，cy，r，h的接近程度。通常来说上下帧之间移动距离不会相差太远，所以坐标越接近就越可能是同一个目标。如何衡量两者之间的距离呢？
cx,cy,h是像素级的数值，而 r 宽高比 是一个比例，可能是零点几的数值，所以四者之间数量级不一样有差距，而且他们之间也不是相互独立的，存在相关性（比如r和h）。DeepSORT采取马氏距离来计算，用马氏距离就需要提供cx,cy,r,h的协方差矩阵（在卡尔曼滤波中，卡尔曼滤波的测量方程，测量空间的协方差矩阵，卡尔曼更新过程中把协方差矩阵提供给数据关联）
马氏距离相当于把不在一个量级且相互关联的状态变量变成不相关联的正太分布。这样求解距离就有了标准。

2.2 余弦距离

2.3 综合使用并调整权重

实际中代码使用lambda=0。为什么会这样呢? 其实马氏距离只起了一个作用，就是剔除错误分配----剔除两个距离很远的框匹配成功的情况，因为距离很远的框即便匹配成功但是阈值判断条件是不符合的，所以通过马氏距离就能把这种失误情况给剔除。所以实际匈牙利算法解决多个跟踪框和多个匹配框之间的最佳匹配问题。求解任务分配问题的过程中只考虑了余弦距离不再考虑马氏距离。

在DeepSort中马氏距离最终用于筛选掉不符合要求的框，而余弦距离才是作为真正的代价矩阵的计算。

3. 级联匹配

但注意也不是完全没用了，主要是通过阈值矩阵（Gate Matrix）对代价矩阵（Cost Matrix）做了一次阈值限制。
接下来就是数据关联，由上面的代价矩阵进行匈牙利匹配。