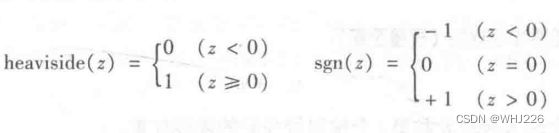机器学习实战（11）——初识人工神经网络

目录

1 感知器

2 多层感知器和反向传播

3 用TensorFlow的高级API训练MLP

4 使用纯TensorFlow训练DNN

4.1 构建阶段

4.2 执行阶段

5 使用神经网络

---

1 感知器

感知器是最简单的ANN架构之一。它基于一个稍微不同的被称为线性阈值单元（LTU）的人工神经元：输入和输出都是数字，每个输入的连接都有一个对应的权重。LTU会加权求和所有的输入（），然后对求值结果应用一个阶跃函数并产生最后的输出，如下图：

感知器中最常见的阶跃函数是Heaviside阶跃函数，如下：

单个LTU可以用来做简单的线性二值分类。它计算输入的线性组合，如果结果超出了阈值，输出就是正，反之则为负。训练LTU的意思是寻找  和  的正确值。

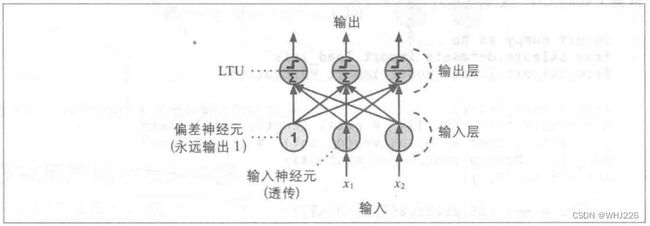
感知器就是个单层的LTU，每个神经元都与所有输入相连。这些连接通常使用称为输入神经元的特殊传递神经元来表示：输入什么就输出什么。此外，还会加上一个额外的偏差特征（）。偏差特征通常用偏差神经元来表示，永远都只输出1。

图中感知器可以将实例同时分为三个不同的二进制类，因此它被称为多输出分类器。

感知器怎么训练呢？当两个神经元有相同的输出时，它们之间的连接权重就会增强。感知器就是使用这个规则的变体进行训练。

感知器学习规则

因为每个输出神经元的决策边界是线性的，所以感知器无法学习复杂的模式。

Scikit-Learn提供了一个实现单一LTU网络的Perceptron类。基本可以在鸢尾花数据集上应用：

首先我们导入常规模块和可视化设置：

# Common imports
import numpy as np
import os

# 以下代码可以确保程序再次运行时结果保持不变
def reset_graph(seed=42):
    tf.compat.v1.reset_default_graph()
    tf.compat.v1.set_random_seed(seed)
    np.random.seed(seed)

# To plot pretty figures
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12

import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron

iris = load_iris()
X = iris.data[:, (2, 3)]  # 花瓣长度和宽度特征
y = (iris.target == 0).astype(np.int) #y = (iris.target == 0)返回的是布尔类型数组，astype(np.int)将True转化为1，将False转化为0

per_clf = Perceptron(max_iter=100, tol=-np.infty, random_state=42)
per_clf.fit(X, y)

y_pred = per_clf.predict([[2, 0.5]])

y_pred

运行结果如下：

array([1])

a = -per_clf.coef_[0][0] / per_clf.coef_[0][1]
b = -per_clf.intercept_ / per_clf.coef_[0][1]

axes = [0, 5, 0, 2]

x0, x1 = np.meshgrid(
        np.linspace(axes[0], axes[1], 500).reshape(-1, 1),
        np.linspace(axes[2], axes[3], 200).reshape(-1, 1),
    )
#X, Y = np.meshgrid(x, y) 代表的是将x中每一个数据和y中每一个数据组合生成很多点,然后将这些点的x坐标放入到X中,y坐标放入Y中,并且相应位置是对应的

X_new = np.c_[x0.ravel(), x1.ravel()] #扁平化作用
y_predict = per_clf.predict(X_new)
zz = y_predict.reshape(x0.shape)

plt.figure(figsize=(10, 4))
#X[y==0, 0]代表标签值即y==0时的坐标的x值，X[y==0, 1]代表标签值即y==0时的坐标的y值
plt.plot(X[y==0, 0], X[y==0, 1], "bs", label="Not Iris-Setosa")
plt.plot(X[y==1, 0], X[y==1, 1], "yo", label="Iris-Setosa")

plt.plot([axes[0], axes[1]], [a * axes[0] + b, a * axes[1] + b], "k-", linewidth=3)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#9898ff', '#fafab0'])

plt.contourf(x0, x1, zz, cmap=custom_cmap) #用来画出不同分类的边界线，也常常用来绘制等高线
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="lower right", fontsize=14)
plt.axis(axes)

plt.show()

运行结果如下：

简洁版如下（掌握）：

a = -per_clf.coef_[0][0] / per_clf.coef_[0][1]
b = -per_clf.intercept_ / per_clf.coef_[0][1]

axes = [0, 5, 0, 2]

plt.figure(figsize=(10, 4))
#X[y==0, 0]代表标签值即y==0时的坐标的x值，X[y==0, 1]代表标签值即y==0时的坐标的y值
plt.plot(X[y==0, 0], X[y==0, 1], "bs", label="Not Iris-Setosa")
plt.plot(X[y==1, 0], X[y==1, 1], "yo", label="Iris-Setosa")

plt.plot([axes[0], axes[1]], [a * axes[0] + b, a * axes[1] + b], "k-", linewidth=3)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="lower right", fontsize=14)
plt.axis(axes)

plt.show()

运行结果如下：

注意，和逻辑回归分类器相反，感知器不输出某个类的概率。它只根据一个固定的阈值来做预测。

感知器无法处理一些很微小的问题，比如异或分类问题。不过可以通过将多个感知器堆叠起来的方式来消除，这种形式的ANN就是多层感知器（MLP,Multi-Layer Perceptron）。 

2 多层感知器和反向传播

一个MLP包含一个（透传）输入层，一个或者多个被称为隐藏层的LTU层，以及一个被称为输出层的LTU组成的最终层，如下图。除了输出层之外，每层都包含了一个偏移神经元，并且与下一层完全相连。

反向传播训练算法，我们称其为反向自动微分的梯度下降。对于每一个训练实例，算法将其发送到网络中并计算每个连续层中每个神经元的输出（这是正向过程，与做预测的过程一样）。然后它会度量网络的输出误差（对比期望值和实际的网络输出），然后它会计算最后一个隐藏层中每个神经元对输出神经元的误差贡献度。之后它继续测量这些误差贡献中有多少来自前一个隐藏层中的每个神经元，这个过程一直持续到输入层。这个反向传递过程通过在网络中向后传播误差梯度有效地测量网络中所有连接权重的误差梯度。

简而言之，对于每个训练实例，反向传播算法先做一次预测（正向过程），度量误差，然后反向的遍历每个层次来度量每个连接的误差贡献度（反向过程），最后再微调每个连接的权重来降低误差（梯度下降） 。

反向传播算法可以和其他激活函数一起使用，最流行的两个激活函数是：

双曲正切函数：

这是一个S形曲线，连续且可微分，不过它的输出值是-1到1之间的值（逻辑是0到1之间的值），这会让每层的输出在训练开始时或多或少地标准化。

ReLU函数：

这个函数也是连续的，不过在z=0时不可微分。不过在实践中它工作良好，而且计算速度快。最重要的是，由于它没有最大输出值，对于消除梯度下降的一些问题很有帮助。

激活函数和他们的导数

MLP常常用来做分类，每个输出对应一个不同的二进制分类（比如，垃圾邮件/正常邮件）。

3 用TensorFlow的高级API训练MLP

用TensorFlow训练MLP的最简单方式是使用它的高级API TF.Learn。用DNNClassifier类来训练一个有着任意数量隐藏层，并包含一个用来计算类别概率的softmax输出层的深度神经网络都易如反掌。

下面的代码训练一个用于分类有两个隐藏层（一个有300个神经元，另外一个有100个），以及一个softmax输出层的具有10个神经元的DNN：

import tensorflow as tf

(X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data()
X_train = X_train.astype(np.float32).reshape(-1, 28*28) / 255.0
X_test = X_test.astype(np.float32).reshape(-1, 28*28) / 255.0
y_train = y_train.astype(np.int32)
y_test = y_test.astype(np.int32)
X_valid, X_train = X_train[:5000], X_train[5000:]
y_valid, y_train = y_train[:5000], y_train[5000:]


feature_cols = [tf.feature_column.numeric_column("X", shape=[28 * 28])]
#实例化
dnn_clf = tf.estimator.DNNClassifier(hidden_units=[300,100], n_classes=10,
                                     feature_columns=feature_cols)

input_fn = tf.compat.v1.estimator.inputs.numpy_input_fn(
    x={"X": X_train}, y=y_train, num_epochs=40, batch_size=50, shuffle=True)
dnn_clf.train(input_fn=input_fn)


test_input_fn = tf.compat.v1.estimator.inputs.numpy_input_fn(
    x={"X": X_test}, y=y_test, shuffle=False)
eval_results = dnn_clf.evaluate(input_fn=test_input_fn)

eval_results

运行结果如下：

{'accuracy': 0.9508,
 'average_loss': 0.17801309,
 'loss': 0.17675847,
 'global_step': 44000}

代码讲解：

1. reshape(m,n)：

#reshape(1,-1)转化成1行

#reshape(2,-1)转换成两行

#reshape(-1,1)转换成1列

#reshape(-1,2)转化成两列

#reshape(2,3)转化成两行三列

2. tf.feature_column.numeric_column:

特征列 (juejin.im)

Graph Execution 入门 (juejin.im)

知识传送门在上。

3. tf.estimator.DNNClassifier：（Premade Estimators (juejin.im)）

# 创建一个有两个隐藏层和每层10个节点的 DNN 
classifier = tf.estimator.DNNClassifier(
    feature_columns=my_feature_columns,
    # 两个隐藏层，每层 10 个节点。
    hidden_units=[10, 10],
    # 模型必须在 3 个类别中作出选择
    n_classes=3)

4. tf.estimator.inputs.numpy_input_fn：

def numpy_input_fn(x,
                   y=None,
                   batch_size=128,
                   num_epochs=1,
                   shuffle=None,
                   queue_capacity=1000,
                   num_threads=1):
#x是训练数据，使用numpy_input_fn时就是numpy array的格式。使用Pandas的时候就是dataframe的格式。

#y是标签。

#batch_size，每一次迭代的时候选择的样本个数，默认选择是128个样本。

#num_epochs，一个epoch是指把整个数据集训练一次。

# epoch=None,steps=100,batch_size=128：
# 当epoch=None的时候就是说，训练的停止条件是达到迭代次数100。（这个时候其实可以算得到整个数据集被训练了100/（3328/128)=3.84次）

# epoch=1,steps=100,batch_size=128:
# 整个数据集共3328条数据，batch_size为128，所以迭代26次（3328/128）时可以实现整个数据集被训练了一次，所以实际上迭代26次就停止训练了。

# epoch=4,steps=100,batch_size=128:
# 和上面类似，只不过这里的epoch=4,故数据集总共需要被训练4次，故迭代次数总共需要4*(3328/128)=104次，但是104>100次，所以100次的时候训练也停止了。

# epoch=100,steps=None,batch_size=128:

# 这个时候steps不指定意味着停止条件是达到epoch的次数。所以当整个数据集被训练了100次的时候停止训练。此时的迭代次数其实是（3328/128)*100=2600次。

#shuffle打乱数据集。

参考：Tensorflow学习-自定义模型_kingsam_的博客-CSDN博客_tensorflow自定义模型

4 使用纯TensorFlow训练DNN

首先是构建阶段，建立TensorFlow的计算图，第二步是执行阶段，运行这个图来训练模型。

4.1 构建阶段

首先需要指定输入和输出的个数，并设置每层的隐藏神经元的个数：

import tensorflow as tf

n_inputs = 28*28  # MNIST
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10

接下来，我们可以使用占位符节点来表示训练数据和目标。X的形状只做了部分定义。我们知道它会是一个二维的张量（一个矩阵），一个维度是实例，另一个维度是特征，我们还知道特征的数量为28×28（每个像素一个特征），但是我们还不知道每个训练批次将包含多少实例。因此X的形状为（None,n_inputs）。类似的我们知道y是一个一维张量，每个实例都有一个入口，但是我们现在还不知道训练批次的大小，所以形状也是 None。

reset_graph()
tf.compat.v1.disable_eager_execution()

X = tf.compat.v1.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.compat.v1.placeholder(tf.int32, shape=(None), name="y")

现在我们来创建神经网络。占位符节点X将用作输入层；在执行期间，它每次都会被训练批次替换（注意训练批次中的所有实例将由神经网络同时处理）。然后我们需要创建两个隐藏层和一个输出层。两个隐藏层基本是一样的：唯一区别是他们和谁连接，以及每层中包含的神经元数量。输出层也一样，不过它会用softmax而不是ReLU作为激活函数。我们创建一个neuron_layer()函数来每次创建一个层。它需要的参数把包括：输入、神经元数量、激活函数、层次的名字：

def neuron_layer(X, n_neurons, name, activation=None):
    with tf.name_scope(name):#通过层的名称来创建一个作用域，它将包含该层的所有计算机节点
        n_inputs = int(X.get_shape()[1])#通过查看输入矩阵的形状并获取第二个维度（第一个维度对应的实例）的尺寸来决定输入的数量
        stddev = 2 / np.sqrt(n_inputs)
        init = tf.compat.v1.truncated_normal((n_inputs, n_neurons), stddev=stddev)
        W = tf.Variable(init, name="kernel")#创建一个保存权重矩阵的变量W。它是一个二维张量包含了每个输入和每个神经元间连接的权重，因此它的形状是(n_inputs, n_neurons)
        b = tf.Variable(tf.zeros([n_neurons]), name="bias")#变量b表示偏差，初始化为0
        Z = tf.matmul(X, W) + b #创建一个子图，该向量实现仅通过一次计算就能够有效计算每层的每个神经元的输入加上偏差项的权重之和。
        if activation is not None:#如果激活函数参数设置了“relu”，代码会返回relu(z)即max(0,z)，否则直接返回z
            return activation(Z)
        else:
            return Z

现在我们可以用该函数创建一个深度神经网络。第一个隐藏层需要X作为其输入。第二层则以第一层的输出作为输入。最后输出层以第二层的输出作为输入：

with tf.name_scope("dnn"):
    hidden1 = neuron_layer(X, n_hidden1, name="hidden1",
                           activation=tf.nn.relu)
    hidden2 = neuron_layer(hidden1, n_hidden2, name="hidden2",
                           activation=tf.nn.relu)
    logits = neuron_layer(hidden2, n_outputs, name="outputs")

注意我们又使用了命名空间来保持名字的清晰。另外，logits是经过softmax激活函数之前神经网络的输出：基于优化的考虑，我们将在稍后处理softmax计算。

TensorFlow提供了很多便利的函数来创建标准神经网络层，所以通常无须定义自己的neuron_layer()函数。比如TensorFlow的fully_connected()函数会创建全连接层，其中所有输入都连接到该层中的所有神经元。这个函数会创建权重和偏差变量，使用合适的初始化策略，使用ReLU激活函数(可以通过activation_fn参数来修改)。它还支持规则化和归一化参数。我们用fully_ connected()函数来替换自己写的neuron_layer()函数，只需要导入函数并替换掉DNN的构造即可:

首先：

pip install --upgrade tf-slim

from tf_slim.layers import fully_connected

with tf.name_scope("dnn"):
    hidden1 = fully_connected(X, n_hidden1, scope="hidden1",
                           activation_fn=tf.nn.relu)
    hidden2 = fully_connected(hidden1, n_hidden2, scope="hidden2",
                           activation_fn=tf.nn.relu)
    logits = fully_connected(hidden2, n_outputs, scope="outputs")

我们已经有了神经网络模型，现在需要定义成本函数用以训练它。我们这里会使用交叉熵。之前讨论过，交叉熵会处罚那些估计目标类的概率较低的模型。TensorFlow提供了很多函数来计算交叉熵，我们这里会用spare_ soft_ max_cross_entropy_with_logits () : 它会根据"logits"来计算交叉熵(比如，在通过softmax激活函数之前网络的输出)，并且期望以0到分类个数减1的整数形式标记(在我们的例子中是从0到9)。这会计算出一个包含每个实例的交叉熵的一维张量。可以使用TensorFlow的reduce_mean()函数来计算所有实例的平均交叉熵。

with tf.name_scope("loss"):
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,
                                                              logits=logits)
    loss = tf.reduce_mean(xentropy, name="loss")

现在我们有了神经网络模型，有了成本函数，下面来定义一个梯度下降优化器 (GradientDescentOptimizer) ，这个优化器会调整模型的参数来使得成本函数的值最小化。

learning_rate = 0.01

with tf.name_scope("train"):
    optimizer = tf.compat.v1.train.GradientDescentOptimizer(learning_rate)
    training_op = optimizer.minimize(loss)

构建期的最后一个重要步骤是指定如何对模型求值。我们简单地将精度用作性能指标。首先，对于每个实例，通过检查最高logit值是否对应于目标类来确定神经网络的预测是否正确。这里可以使用in_top_k()函数，这个函数会返回一个一维的张量，其值为布尔类型，因此我们需要将值强制装换成浮点型然后计算平均值，这会得出网络的总体精度。

with tf.name_scope("eval"):
    correct = tf.compat.v1.nn.in_top_k(logits, y, 1)
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

这里有参考：tensorflow之版本问题 in_top_k 报错_Abandon_first的博客-CSDN博客

我们创建节点初始化变量，创建Saver将训练后的模型保存到磁盘：

init = tf.compat.v1.global_variables_initializer()
saver = tf.compat.v1.train.Saver()

我们创建了用于输入和目标值占位符节点，创建了用以创建神经网络的函数，使用它创建DNN，定义了成本函数，创建了一个优化器，最后还定义了性能度量。现在我们进入执行期。

4.2 执行阶段

首先，加载MNIST数据集：

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data")

如果报错，解决方案在此：No module named ‘tensorflow.examples‘解决方案_beyond谚语的博客-CSDN博客

然后定义需要运行的epoch数量，以及小批次大小:

n_epochs = 40
batch_size = 50

def shuffle_batch(X, y, batch_size):
    rnd_idx = np.random.permutation(len(X))
    n_batches = len(X) // batch_size
    for batch_idx in np.array_split(rnd_idx, n_batches):
        X_batch, y_batch = X[batch_idx], y[batch_idx]
        yield X_batch, y_batch

训练模型：

with tf.compat.v1.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
            sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
        acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
        acc_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
        print(epoch, "Batch accuracy:", acc_batch, "Val accuracy:", acc_val)

    save_path = saver.save(sess, "E:/PYTHON/my_model_final.ckpt")

运行结果如下：

0 Batch accuracy: 0.82 Val accuracy: 0.8382
1 Batch accuracy: 0.86 Val accuracy: 0.8768
2 Batch accuracy: 0.88 Val accuracy: 0.8908
3 Batch accuracy: 0.86 Val accuracy: 0.9078
4 Batch accuracy: 0.92 Val accuracy: 0.917
5 Batch accuracy: 0.9 Val accuracy: 0.925
6 Batch accuracy: 0.78 Val accuracy: 0.9328
7 Batch accuracy: 0.96 Val accuracy: 0.9388
8 Batch accuracy: 0.98 Val accuracy: 0.9442
9 Batch accuracy: 0.92 Val accuracy: 0.9448
10 Batch accuracy: 0.98 Val accuracy: 0.9476
11 Batch accuracy: 0.86 Val accuracy: 0.9522
12 Batch accuracy: 0.98 Val accuracy: 0.9532
13 Batch accuracy: 0.96 Val accuracy: 0.956
14 Batch accuracy: 0.96 Val accuracy: 0.9594
15 Batch accuracy: 0.98 Val accuracy: 0.9592
16 Batch accuracy: 0.98 Val accuracy: 0.9588
17 Batch accuracy: 1.0 Val accuracy: 0.958
18 Batch accuracy: 0.94 Val accuracy: 0.9642
19 Batch accuracy: 0.98 Val accuracy: 0.9644
20 Batch accuracy: 0.98 Val accuracy: 0.9668
21 Batch accuracy: 0.98 Val accuracy: 0.9696
22 Batch accuracy: 0.9 Val accuracy: 0.967
23 Batch accuracy: 0.96 Val accuracy: 0.9704
24 Batch accuracy: 1.0 Val accuracy: 0.9724
25 Batch accuracy: 0.96 Val accuracy: 0.974
26 Batch accuracy: 0.96 Val accuracy: 0.9728
27 Batch accuracy: 0.98 Val accuracy: 0.9732
28 Batch accuracy: 1.0 Val accuracy: 0.9766
29 Batch accuracy: 0.98 Val accuracy: 0.9732
30 Batch accuracy: 0.98 Val accuracy: 0.9768
31 Batch accuracy: 1.0 Val accuracy: 0.976
32 Batch accuracy: 1.0 Val accuracy: 0.9776
33 Batch accuracy: 0.98 Val accuracy: 0.9798
34 Batch accuracy: 0.98 Val accuracy: 0.9814
35 Batch accuracy: 1.0 Val accuracy: 0.9834
36 Batch accuracy: 1.0 Val accuracy: 0.9822
37 Batch accuracy: 0.98 Val accuracy: 0.9816
38 Batch accuracy: 0.98 Val accuracy: 0.9806
39 Batch accuracy: 0.98 Val accuracy: 0.9848

上面的代码先打开了一个TensorFlow的会话，运行初始化代码来初始化所有的变量。运行主训练循环：在每一个周期(epoch)中，选代一组和训练集大小相对应的批次，每一个小批次通过next_batch()方法来获得，然后执行训练操作，将当前小批次的输入数据和目标传入。接下来，在每个周期结束的时候，代码会用上一个小批次以及全量的训练集来评估模型,并打印结果。最后，将模型的参数保存到硬盘。

5 使用神经网络

现在我们用训练好的神经网络进行预测：

with tf.compat.v1.Session() as sess:
    saver.restore(sess, "E:/PYTHON/my_model_final.ckpt") # or better, use save_path
    X_new_scaled = X_test[:20]
    Z = logits.eval(feed_dict={X: X_new_scaled})
    y_pred = np.argmax(Z, axis=1)

报错：

ValueError: Cannot feed value of shape (20, 28, 28) for Tensor X:0, which has shape (None, 784)

翻找各大博主的博文时要么没有给出以上代码的结果要么运行成功了，具体原因还在查找中。

上面的代码首先从硬盘上加载模型参数，然后加载需要被分类的新图片。记住应用与训练数据相同的特征缩放(这里是从0到1)。然后评估logits节点。如果我们想知道所有分类的概率，可以给logits使用softmax()函数，如果只是想预测一个分类，只需要选出那个有最大logit值的即可(可以使用argmax()函数完成)。

学习笔记——《机器学习实战：基于Scikit-Learn和TensorFlow》