【论文阅读】BEVFormer: Learning Bird’s-Eye-View Representation from Multi-Camera Images via Spatiotemporal
论文题目:BEVFormer: Learning Bird’s-Eye-View Representation from Multi-Camera Images via Spatiotemporal Transformers
-
参考与前言
arXiv 地址:
BEVFormer: Learning Bird’s-Eye-View Representation from Multi-Camera Images via Spatiotemporal Transformers
github代码地址(还没开,六月开):https://github.com/zhiqi-li/BEVFormer
整篇文章方法挺清晰的 理解起来不费劲
1. Motivation
做的任务是:3D detection,主要是提出使用BEV的表达方式去做感知类任务
问题场景
Perception in 3D space
因为整篇是拿相机在做表达和任务,所以先是说明相机优势:identify vision-based road elements (e.g., traffic lights, stoplines);指出BEV优势:清晰的表述了物体的位置和大小,比较适合自动驾驶里感知和规划的任务,同时连接了 temporal 和 spatial space,时空两个空间
同时指出现有的BEV方案:1. 2D plane,2. 从深度信息获取特征,对深度值和深度分布太敏感
因为基于BEV方法的detection performance 会受 compounding error和BEV特征的影响,所以我们提出了一种 不受深度信息,同时无需严格依靠3d prior 学习BEV的方法
Contribution
- 提出一种 以多相机和时间作为输入的,时空transformer encoder
We propose BEVFormer, a spatiotemporal transformer encoder that projects multi-camera and/or timestamp input to BEV representations. - 设计了通过在空间上的cross-attention,和时间上的self-attention,设计 learnable BEV queries 去做时域上的结合,然后加到Unified BEV 特征中
- 做nuScenes和Waymo的detection任务重取得了不错的效果
相关工作中介绍了 基于transformer-based 2D perception,和基于相机的 3D Perception
问题区:
-
cross-camera post-processing
是指将相机进行坐标转换 把数据对其嘛?还是啥? → 好像就是多相机的处理
-
3d prior是指不同相机之间的外参嘛?所以是指的是减弱外参在整个框架中的先验?
2. Method
2.1 框架
框架图挺清晰,从输入是六个角度的相机,通过一个可选的backbone(比如resnet101)
- 每张照片都得到一个 feature F t i F_t^i Fti 其中 i 指代第 i 个相机,合起来就是得到一个 F t = { F t i } i = 1 N view F_t=\{F_t^i\}_{i=1}^{N_{\text{view}}} Ft={Fti}i=1Nview
- BEV Queries Q 是 gird-shaped learnable parameter Q ∈ R H × W × C Q \in \R^{H\times W \times C} Q∈RH×W×C H, W就是空间下BEV平面的大小,在 点 p = ( x , y ) p=(x, y) p=(x,y) 下的 Q p ∈ R 1 × C Q_p \in \R^{1 \times C} Qp∈R1×C 和其对应的BEV plane grid cell region有关,每个格都代表现实世界中s米的范围长度(s分辨率
对 queries Q里同样加入learnable的positional embedding

2.2 Spatial Cross-Attention 空间域
过程可以用该公式概括:
SCA ( Q p , F t ) = 1 ∣ V hit ∣ ∑ i ∈ V hit ∑ j = 1 N ref DeformAttn ( Q p , P ( p , i , j ) , F t i ) \operatorname{SCA}\left(Q_{p}, F_{t}\right)=\frac{1}{\left|\mathcal{V}_{\text {hit }}\right|} \sum_{i \in \mathcal{V}_{\text {hit }}} \sum_{j=1}^{N_{\text {ref }}} \operatorname{DeformAttn}\left(Q_{p}, \mathcal{P}(p, i, j), F_{t}^{i}\right) SCA(Qp,Ft)=∣Vhit ∣1i∈Vhit ∑j=1∑Nref DeformAttn(Qp,P(p,i,j),Fti)
对于每个 Q p Q_p Qp 我们都有一个project function P ( p , i , j ) \mathcal P(p,i,j) P(p,i,j) 以获取 i-th相机下的 j-th 参考点
从现实坐标 ( x ′ , y ′ ) (x',y') (x′,y′) 中 找到对应的query p=(x,y) 下 Q p Q_p Qp :
x ′ = ( x − W 2 ) × s ; y ′ = ( y − H 2 ) × s x^{\prime}=\left(x-\frac{W}{2}\right) \times s ; \quad y^{\prime}=\left(y-\frac{H}{2}\right) \times s x′=(x−2W)×s;y′=(y−2H)×s
同时因为在(x’,y’)上的物体也会有z上的高度,所以对于每个query Q p Q_p Qp 我们会得到 a pillar of 3D 参考点 ( x ′ , y ′ , z j ′ ) j = 1 N r e f \left(x^{\prime}, y^{\prime}, z_{j}^{\prime}\right)_{j=1}^{N_{\mathrm{ref}}} (x′,y′,zj′)j=1Nref 然后通过projection matrix投到对应的相机下
P ( p , i , j ) = ( x i j , y i j ) where z i j ⋅ [ x i j y i j 1 ] T = T i ⋅ [ x ′ y ′ z j ′ 1 ] T \mathcal{P}(p, i, j)=\left(x_{i j}, y_{i j}\right)\\\text{where }z_{i j} \cdot\left[\begin{array}{lll}x_{i j} & y_{i j} & 1\end{array}\right]^{T}=T_{i} \cdot\left[\begin{array}{llll}x^{\prime} & y^{\prime} & z_{j}^{\prime} & 1\end{array}\right]^{T} P(p,i,j)=(xij,yij)where zij⋅[xijyij1]T=Ti⋅[x′y′zj′1]T
其中 T i ∈ R 3 × 4 T_i \in \R^{3\times 4} Ti∈R3×4 就是第i个相机的projection matrix
2.3 Temporal Self-Attention 时间域
主要是要拿上一个输出的 BEV B t B_t Bt 作为输入
TSA ( Q p , { Q , B t − 1 ′ } ) = ∑ V ∈ { Q , B t − 1 ′ } DeformAttn ( Q p , p , V ) \operatorname{TSA}\left(Q_{p},\left\{Q, B_{t-1}^{\prime}\right\}\right)=\sum_{V \in\left\{Q, B_{t-1}^{\prime}\right\}} \operatorname{DeformAttn}\left(Q_{p}, p, V\right) TSA(Qp,{Q,Bt−1′})=V∈{Q,Bt−1′}∑DeformAttn(Qp,p,V)
不同于vanilla deformable attention,这个offsets Δ p \Delta p Δp 是从此处 concate { Q , B ’ t − 1 } \{Q, B’_{t-1}\} {Q,B’t−1} 预测而出
问题区:
-
R-101 DCN 没找到… 搜了一下 相关Github
是resnet 101 卷积核可变吗?【15, 12】 实验中 用了两个backbone进行对比
-
projection matrix是到车中心?
只要是一个中心就行…
-
开始咋处理? 上一帧输入 BEV B t B_t Bt
重复 Q,{Q, Q}
3. 实验及结果
实现细节上:
- 选择t时,是从相邻2s时间内随机采样而来,减少ego-motion的diversity,比如四个采样: t − 3 , t − 2 , t − 1 , t t-3,t-2,t-1, t t−3,t−2,t−1,t,由此可得到: { B t − 3 , B t − 2 , B t − 1 } \left\{B_{t-3}, B_{t-2}, B_{t-1}\right\} {Bt−3,Bt−2,Bt−1}
- 因为 B t B_t Bt 是基于多相机and B t − 1 B_{t-1} Bt−1的,所以 B t B_t Bt 包含four samples的时空域clues
Loss function是根据 任务定义而来的,比如detection、segmentation等
结果表
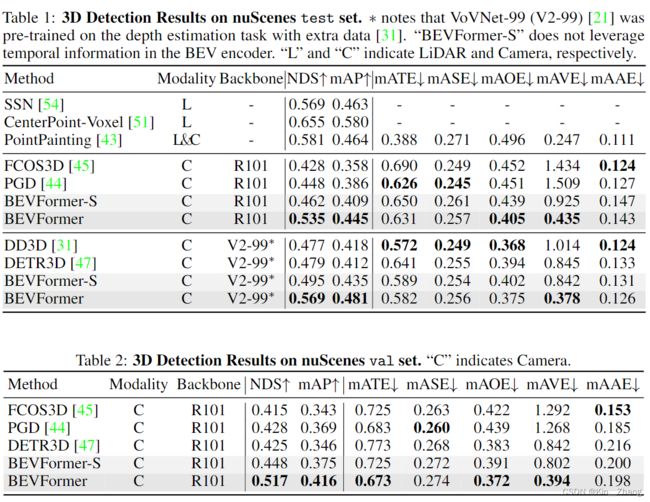
nuScenes 数据集

waymo数据集

4. Conclusion
提出BEVFormer,验证其效果不错
limitation中提到了 和LiDAR-based还是有gap的,主要在effect和efficiency上(但是其实在本文表1 pointpaiting也并没有 … effect上比BEVFormer好?可能只是这种指标下

碎碎念
代码还没开,可以等一波,但是好像知乎有人讨论说 也不一定会按时开。先就大概看看,网络方法输入输出都挺清晰的,就是感觉 emmm 效果意外的好 hhh
- 有些细节有点迷,比如x’,y’获取是内参+外参直接pixel到全局坐标系下吗?
- 估计后面跑跑 debug一下理解更深点
不同的方法对时间域数据上的处理方式各不相同,感觉时间域上的玩法还挺多的,比如上次MP3里面是optical flow, interesting;这种在视频领域更多一点 上次看沐神b站上有讲过I3D 3D-conv

赠人点赞 手有余香 ;正向回馈 才能更好开放记录 hhh