三种图像内插法（最近邻内插法、双线性内插法、双三次内插法）的做法 & 代码实现

参考博客

数字图像处理学习笔记（四）——数字图像的内插、度量、表示与质量_闭关修炼——暂退的博客-CSDN博客

数字图像处理学习笔记（七）——用Pycharm及MATLAB实现三种图像内插法（最近邻内插法、双线性内插法、双三次内插法）_闭关修炼——暂退的博客-CSDN博客

数字图像的内插

内插是在诸如放大、收缩、旋转和几何校正等任务中广泛应用的基本工具。
从根本上看，内插是用已知数据来 估计未知位置的数值的处理。
实现图像内插的方法有三种： 最近邻内插法、双线性内插法、双三次内插法 。

最近邻内插法

理解：在原图像中寻找最接近的像素，并把该像素的灰度赋给加想要创建大小的网格中的新像素。
当我们完成对网格中覆盖的所有点的灰度赋值后，就把图像扩展到原来规定的大小，得到放大后的图像。
本方法不常用是因为会产生不希望的人为缺陷的倾向（如某些直边缘的严重失真）。

双线性内插法

赋于点（x,y）灰度值公式：v(x,y)=ax+by+cxy+d

注：与该方法名称相反的是，双线性内插不是一种线性内插方法，因为其中包含有xy项。
       4个系数可由4个用（x,y）点最近邻点写出的未知方程确定（四个未知数四个方程）。
       双线性内插法给出了比最近邻内插好得多的结果，但随之而来的是计算量的增加。

双三次内插法

赋于点（x,y）灰度值公式：

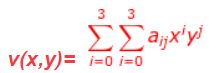
注：双三次内插包括16个最近邻点。
       16个系数可由16个用（x,y）点最近邻点写出的未知方程式确定。
     如果求和的上下限为1和0时，那么就变成了双线性内插v(x,y)=ax+by+cxy+d公式的形式。
        通常，双三次内插在保持细节方面比双线性内插相对较好，但其计算量非常大。
        双三次内插是商业图像编辑程序的标准内插方法。

数字图像的度量

关于数字图像的度量，有欧氏距离、曼哈顿距离、切比雪夫距离之分。

对于坐标分别为（x,y）,（s,t）,（v,w）的像素p，q，z。

欧几里得（欧式）距离：

 
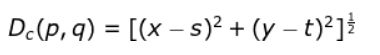
注：距点（x,y）的距离小于等于某个值r的像素是中心在（x,y）且半径为r的圆平面。

D4（又称城市街区、曼哈顿）距离：

 
注：距点（x,y）的距离小于等于某个值r的像素形成一个中心在（x,y）的菱形.
例如距中心点（x,y）的距离小于等于2的像素，形成固定距离的如右图轮廓，其中=1的像素是（x,y）的4领域。：

 

D8（又称切比雪夫、棋盘）距离：

 
注：距点（x,y）的距离小于等于某个值r的像素形成一个中心在（x,y）的方形。

例如距中心点（x,y）的距离小于等于2的像素，形成固定距离的如右图轮廓，其中=1的像素是（x,y）的8领域。

数字图像的表示

二维离散亮度函数——f(x,y)：
        x，y说明图像像素的空间坐标；
        函数值 f 代表了在点(x,y)处像素的灰度值。

二维矩阵——A[m,n]：
        m,n说明图像的宽和高；
        矩阵元素a(i，j)的值，表示图像在第 i 行，第 j 列的像素的灰度值（i,j表示几何位置）。

图像描述信息：如图像高度和宽度等信息。

图像数据：顺序存放的连续数据。

       注：1字节=8位；
              对于2色位图，1位表示一个像素颜色（2=）， 所以一个字节表示8个像素；
              对于16色位图，4位表示一个像素颜色（16=）， 所以一个字节表示2个像素；
              对于256色位图，8位表示一个像素颜色（256=），所以1个字节表示1个像素；
              对于真彩色图，3个字节表示一个像素（因为真彩图有R、G、B三个通道）。
 

数字图像的质量

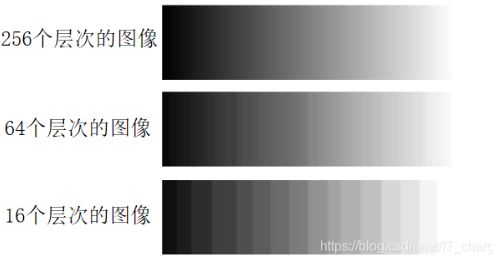
灰度级：表示像素明暗程度的整数量。
    例如：像素的取值范围为0-255，就称该图像为256个灰度级的图像。

层次：表示图像实际拥有的灰度级的数量。
    例如：具有32种不同取值的图像，可称该图像具有32个层次。
图像数据的实际层次越多，视觉效果就越好。

 

对比度：指一幅图像中灰度反差的大小 。

对比度 = 最大亮度 / 最小亮度（即最大像素值/最小像素值）

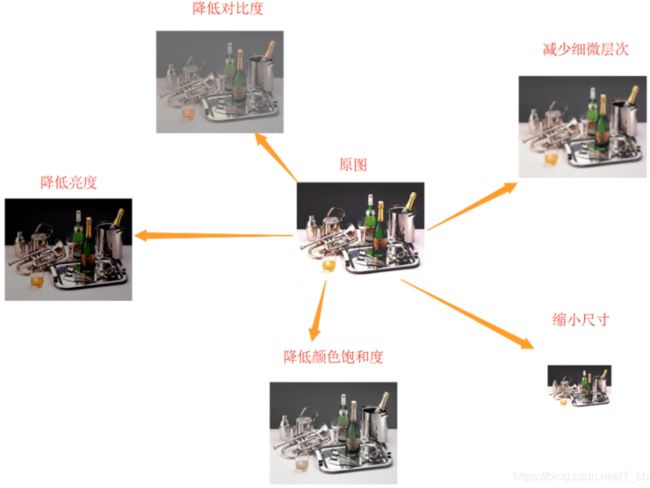
清晰度：与清晰度相关的主要因素：亮度、对比度、尺寸大小、细微层次、颜色饱和度。

python实现

from PIL import Image
import matplotlib.pyplot as plt    
import numpy as np     
import math

def NN_interpolation(img,dstH,dstW):
    scrH,scrW,_=img.shape
    retimg=np.zeros((dstH,dstW,3),dtype=np.uint8)
    for i in range(dstH):
        for j in range(dstW):
            scrx=round((i+1)*(scrH/dstH))
            scry=round((j+1)*(scrW/dstW))
            retimg[i,j]=img[scrx-1,scry-1]
    return retimg

def BiLinear_interpolation(img,dstH,dstW):
    scrH,scrW,_=img.shape
    img=np.pad(img,((0,1),(0,1),(0,0)),'constant')
    retimg=np.zeros((dstH,dstW,3),dtype=np.uint8)
    for i in range(dstH):
        for j in range(dstW):
            scrx=(i+1)*(scrH/dstH)-1
            scry=(j+1)*(scrW/dstW)-1
            x=math.floor(scrx)
            y=math.floor(scry)
            u=scrx-x
            v=scry-y
            retimg[i,j]=(1-u)*(1-v)*img[x,y]+u*(1-v)*img[x+1,y]+(1-u)*v*img[x,y+1]+u*v*img[x+1,y+1]
    return retimg

def BiBubic(x):
    x=abs(x)
    if x<=1:
        return 1-2*(x**2)+(x**3)
    elif x<2:
        return 4-8*x+5*(x**2)-(x**3)
    else:
        return 0

def BiCubic_interpolation(img,dstH,dstW):
    scrH,scrW,_=img.shape
    #img=np.pad(img,((1,3),(1,3),(0,0)),'constant')
    retimg=np.zeros((dstH,dstW,3),dtype=np.uint8)
    for i in range(dstH):
        for j in range(dstW):
            scrx=i*(scrH/dstH)
            scry=j*(scrW/dstW)
            x=math.floor(scrx)
            y=math.floor(scry)
            u=scrx-x
            v=scry-y
            tmp=0
            for ii in range(-1,2):
                for jj in range(-1,2):
                    if x+ii<0 or y+jj<0 or x+ii>=scrH or y+jj>=scrW:
                        continue
                    tmp+=img[x+ii,y+jj]*BiBubic(ii-u)*BiBubic(jj-v)
            retimg[i,j]=np.clip(tmp,0,255)
    return retimg



im_path='/home/jovyan/img/earth.jpg'
image=np.array(Image.open(im_path))

image1=NN_interpolation(image,image.shape[0]*2,image.shape[1]*2)
image1=Image.fromarray(image1.astype('uint8')).convert('RGB')
image1.save('/home/jovyan/img/NNEarth.jpg')

image2=BiLinear_interpolation(image,image.shape[0]*2,image.shape[1]*2)
image2=Image.fromarray(image2.astype('uint8')).convert('RGB')
image2.save('/home/jovyan/img/BiLinearEarth.jpg')

image3=BiCubic_interpolation(image,image.shape[0]*2,image.shape[1]*2)
image3=Image.fromarray(image3.astype('uint8')).convert('RGB')
image3.save('/home/jovyan/img/BiCubicEarth.jpg')

Matlab代码实现

①最近邻插值

% 最近邻插值

% 输入图像文件及放大率
% 输出根据放大率变化后的新图像
function nearest_neighbor = nearest_neighbor(filename,R)


% 初始化，读入图像，图像数据为m*n*color
img = imread('E:\earth.GIF');

% 变化后图像
[row,col,color] = size(img);    % 获得图像的行列数及色板数
row = round(row*0.8);     % 新图像行
col = round(col*0.8);     % 新图像列

% 新图像初始化
% 使用class获得原图像的数据类型，使得新图像数据类型与原图像保持一致
img_new = zeros(row,col,color,class(img));

% 对新图像的行、列、色板赋值
for i = 1:row
    for j = 1:col
        for n = 1:color
            x = round(i/0.8);
            y = round(j/0.8);
            % 为了避免x和y等于0而报错，采取+1处理即可
            if x == 0
                x = x+1;
            end
            if y == 0
                y = y+1;
            end
            img_new(i,j,n) = img(x,y,n);
        end
    end
end

% 显示原图像
figure;
imshow(img);
title("Original Image");

% 显示新图像
figure;
imshow(img_new);
title("New Image");
end

②双线性插值

% 双线性插值

% 输入图像文件及放大率
% 输出根据放大率变化后的新图像
function bilinear_interpolation = bilinear_interpolation(filename,R)

% 初始化，读入图像，图像数据为m*n*color
img = imread('H:\earth.JPG');

% 变化后图像
[row,col,color] = size(img);    % 获得图像的行列数及色板数
row = round(row*0.8);     % 新图像行
col = round(col*0.8);     % 新图像列

% 新图像初始化
% 使用class获得原图像的数据类型，使得新图像数据类型与原图像保持一致
img_new = zeros(row,col,color,class(img));

% 对新图像的行、列、色板赋值
for i = 1:row
    for j = 1:col
        for n = 1:color
            x = round(i/0.8);
            y = round(j/0.8);
            if x == 0
                x = x+1;
            end
            if y ==0
                y = y+1;
            end
            u = i/0.8-floor(i/0.8); %求取水平方向上的权重
            v = j/0.8-floor(j/0.8); %求取垂直方向上的权重

            % 此处需要对图像边缘进行例外处理
            % 本例对图像右边缘及下边缘用最近邻插值计算
            if i >= row-0.8 || j >= col-0.8
                img_new(i,j,n) = img(x,y,n);
            else
                img_new(i,j,n) = u*v*img(x,y,n)+(1-u)*v*img(x+1,y,n)+u*(1-v)*img(x,y+1,n)+(1-u)*(1-v)*img(x+1,y+1,n);
            end
        end
    end
end

% 显示原图像
figure;
imshow(img);
title("Original Image");

% 显示新图像
figure;
imshow(img_new);
title("New Image");

③双三次插值

% 双三次插值

    tic; % calculate running time

    % read original image I
    I = imread('G:\earth.GIF');
    I = double(I);
    [oh,ow,od] = size(I);
    zmf = 2; %缩放因子

    % initial target image TI
    th = round(oh*zmf);
    tw = round(ow*zmf);
    TI = zeros(th,tw,od); %预分配内存提高计算速度

    % add original image with 2 rows and 2 cols
    % expand the border to prevent calculation overflow
    a = I(1,:,:); b = I(oh,:,:);
    temp_I = [a;a;I;b;b];
    c = temp_I(:,1,:); d = temp_I(:,ow,:);
    FI = [c,c,temp_I,d,d];
    
    % fill target image with new pixels
    for w = 1:tw
        j = floor(w/zmf)+2; v = rem(w,zmf)/zmf;
        for h = 1:th
            i = floor(h/zmf)+2;  u = rem(h,zmf)/zmf; 
            A = [s(u+1),s(u),s(u-1),s(u-2)];
            C = [s(v+1);s(v);s(v-1);s(v-2)];
            for d = 1:od   % image's 3 channels    
               B = FI(i-1:i+2,j-1:j+2,d);
               TI(h,w,d) = A*B*C;    
            end
        end
    end
    
    figure;
    imshow(uint8(TI));
    toc;

% 插值核函数
function w = s(wx)
    wx = abs(wx);
    if wx<1
        w = 1 - 2*wx^2 + wx^3;
    elseif wx>=1 && wx<2
        w = 4 - 8*wx + 5*wx^2 - wx^3;
    else
        w = 0;
    end
end