代码随想录算法训练营第21天 | 530.二叉搜索树的最小绝对差 501.二叉搜索树中的众数 236. 二叉树的最近公共祖先

代码随想录系列文章目录

二叉树篇-二叉搜索树

---

530.二叉搜索树的最小绝对差

题目链接
思路，这道题和98.验证二叉搜索树题目链接的思路是一样的，对于二叉搜索树的搜索，都是中序的。代表左中右，里面的数值应该是单调递增的。我们可以把树压成数组，然后对数组进行操作。当然我们也不必要这样做。

在98.验证二叉搜索树的时候，维护了一个当前结点的左孩子的值pre，如果这个pre的值小于当前遍历结点的值，我们把当前结点的值赋给pre; 如果说 pre的值大于当前结点的值，说明它不是BST

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        # 规律: BST的中序遍历节点数值是从小到大. 
        cur_max = -float("INF")   #其实就是node的左边的一个孩子的值, 因为遍历顺序是左中右，也是展开成数组，正在遍历的数的前一个的值
        def __isValidBST(root: TreeNode) -> bool: 
            nonlocal cur_max
            
            if not root: 
                return True
            
            is_left_valid = __isValidBST(root.left)   #左
            if cur_max < root.val:                    #中
                cur_max = root.val
            else: 
                return False
            is_right_valid = __isValidBST(root.right)  #右
            
            return is_left_valid and is_right_valid
        return __isValidBST(root)

在530.二叉搜索树的最小绝对差这道题，依然我们可以维护这么一个pre结点，然后不断的更新维护最小的 node.val - pre.val

中序遍历，设一个pre结点， 维护node.val 和 pre.val的最小差

class Solution:
    def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
        res = 100001
        pre = TreeNode(val = -1)  #之所以把val设成-1,是因为避开树中结点的val
        def rec(node):
            nonlocal res, pre
            if not node: return
            rec(node.left)                                # 左
            if pre.val != -1:          
                res = min(res, node.val - pre.val)        #中
            pre = node
            rec(node.right)                               #右
        rec(root)
        return res

当然，也可以把树压着数组

501.二叉搜索树中的众数

题目链接

第一种思路，把二叉树压成数组，然后建dict，对dict的value进行排序，然后取前面的高频元素

如何对dict中的value进行排序代码中有体现

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findMode(self, root: Optional[TreeNode]) -> List[int]:
        res = []
        def tonums(node):
            if not node: return None
            if node.left: tonums(node.left)
            res.append(node.val)
            if node.right: tonums(node.right)
            return res
        tonums(root)
        
        nums_dict = collections.Counter(res)
        sortednums = sorted(nums_dict.items(),key = lambda x:x[1],reverse = True)
        result = []
        result.append(sortednums[0][0])
        for i in range(1, len(sortednums)):
            if sortednums[i][1] == sortednums[0][1]:
                result.append(sortednums[i][0])
        return result

第二种思路，利用二叉搜索树的特性，设pre

既然是搜索树，它中序遍历就是有序的，如果一个元素重复出现很多次，那么它们一定是连着的。遍历有序数组的元素出现频率，从头遍历，相邻两个元素作比较就能统计出现频率，然后就把出现频率最高的元素输出就可以了。

这个比较有三种：
第一种 pre == None, curr目前是树的最左的结点
if not self.pre: self.count = 1
第二种 pre = curr
elif self.pre.val == cur.val: self.count += 1
第三种 pre != curr
else: self.count = 1
完成比较之后，更新频率count之后，更新pre = curr就好了

下面的操作是，如果 频率count 等于 maxCount（最大频率），要把这个元素加入到结果集中

是不是感觉这里有问题，result怎么能轻易就把元素放进去了呢，万一，这个maxCount此时还不是真正最大频率呢。

所以下面要做如下操作：

频率count 大于 maxCount的时候，不仅要更新maxCount，而且要清空结果集，因为结果集之前的元素都失效了。这样动态更新，只需要遍历一遍二叉树，就在统计频率的同时，完成结果集的更新了。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.pre = TreeNode()
        self.count = 0
        self.max_count = 0
        self.result = []

    def findMode(self, root: TreeNode) -> List[int]:
        if not root: return None
        self.search_BST(root)
        return self.result
        
    def search_BST(self, cur: TreeNode) -> None:
        if not cur: return None
        self.search_BST(cur.left)
        # 第一个节点
        if not self.pre:
            self.count = 1
        # 与前一个节点数值相同
        elif self.pre.val == cur.val:
            self.count += 1 
        # 与前一个节点数值不相同
        else:
            self.count = 1
        self.pre = cur

        if self.count == self.max_count:
            self.result.append(cur.val)
        
        if self.count > self.max_count:
            self.max_count = self.count
            self.result = [cur.val]	# 清空self.result，确保result之前的的元素都失效
        
        self.search_BST(cur.right)

236. 二叉树的最近公共祖先

题目链接
遇到这个题目首先想的是要是能自底向上查找就好了，这样就可以找到公共祖先了。

那么二叉树如何可以自底向上查找呢？回溯啊，二叉树回溯的过程就是从低到上。

后序遍历就是天然的回溯过程，最先处理的一定是叶子节点。

有两种情况：
1.如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先。
2.p或者q本身就是最近公共祖先呢？
但是很多人容易忽略一个情况，就是节点本身是p(q)，它拥有一个子孙节点

使用后序遍历，回溯的过程，就是从低向上遍历节点，一旦发现满足第一种情况的节点，就是最近公共节点了。

其实只需要找到一个节点是p或者q的时候，直接返回当前节点，无需继续递归子树。

如果接下来的遍历中找到了后继节点满足第一种情况则修改返回值为后继节点，否则，继续返回已找到的节点即可。

思路实现

1.参数
2.出口：如果找到了 节点p或者q，或者遇到空节点，就返回。
3.单层递归逻辑：
本题函数有返回值，是因为回溯的过程需要递归函数的返回值做判断，但本题我们依然要遍历树的所有节点。如果递归函数有返回值，如何区分要搜索一条边，还是搜索整个树呢？

搜索一条边的写法：

if (递归函数(root->left)) return ;

if (递归函数(root->right)) return ;

搜索整个树写法：

left = 递归函数(root->left);
right = 递归函数(root->right);
left与right的逻辑处理;

在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）
那么为什么要遍历整棵树呢？直观上来看，找到最近公共祖先，直接一路返回就可以了。

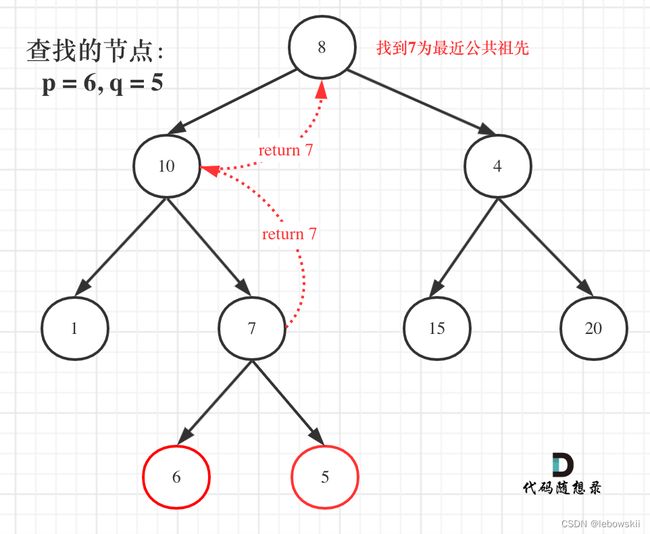
就像图中一样直接返回7，多美滋滋。

但事实上还要遍历根节点右子树（即使此时已经找到了目标节点了），也就是图中的节点4、15、20。

因为在如下代码的后序遍历中，如果想利用left和right做逻辑处理， 不能立刻返回，而是要等left与right逻辑处理完之后才能返回。
所以此时大家要知道我们要遍历整棵树。知道这一点，对本题就有一定深度的理解了。
那么先用left和right接住左子树和右子树的返回值，代码如下：

TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);

如果left 和 right都不为空，说明此时root就是最近公共节点。这个比较好理解

如果left为空，right不为空，就返回right，说明目标节点是通过right返回的，反之依然。

这里有的同学就理解不了了，为什么left为空，right不为空，目标节点通过right返回呢？

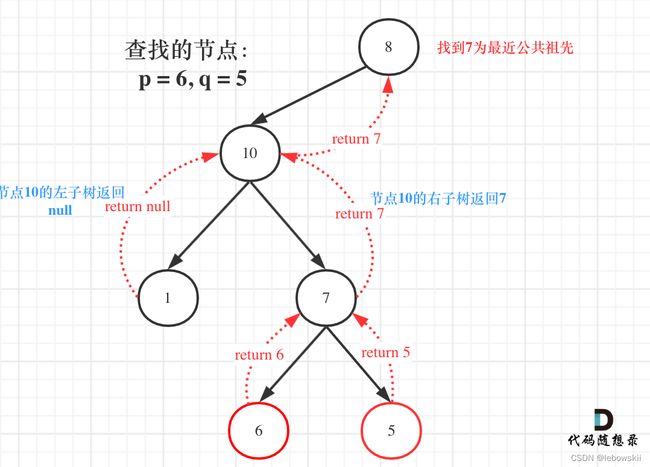
图中节点10的左子树返回null，右子树返回目标值7，那么此时节点10的处理逻辑就是把右子树的返回值（最近公共祖先7）返回上去！

这里点也很重要，可能刷过这道题目的同学，都不清楚结果究竟是如何从底层一层一层传到头结点的。

那么如果left和right都为空，则返回left或者right都是可以的，也就是返回空。

if (left == NULL && right != NULL) return right;
else if (left != NULL && right == NULL) return left;
else  { //  (left == NULL && right == NULL)
    return NULL;
}

那么寻找最小公共祖先，完整流程图如下：

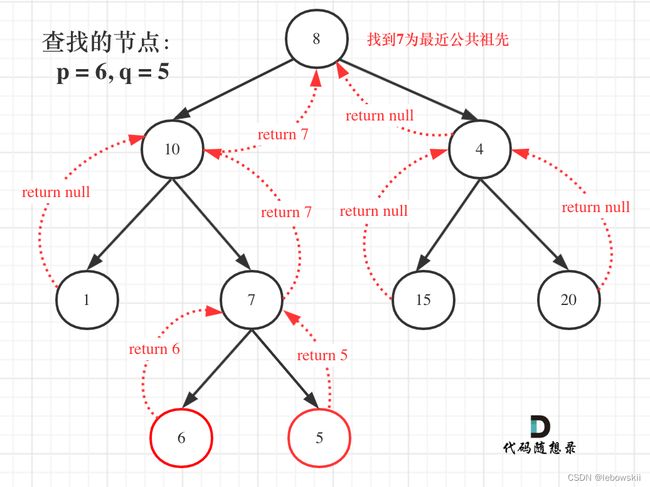
从图中，大家可以看到，我们是如何回溯遍历整棵二叉树，将结果返回给头结点的！

那么卡哥给大家归纳如下三点：

求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从低向上的遍历方式。

在回溯的过程中，必然要遍历整棵二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。

要理解如果返回值left为空，right不为空为什么要返回right，为什么可以用返回right传给上一层结果。

可以说这里每一步，都是有难度的，都需要对二叉树，递归和回溯有一定的理解。

代码实现

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root: return None
        if root == q or root == p: return root
        
        left = self.lowestCommonAncestor(root.left, p, q)      #左
        right = self.lowestCommonAncestor(root.right, p, q)    #右
         
        if left != None and right != None:
            return root
        elif left == None and right != None:
            return right
        elif left != None and right == None:
            return left
        else: return None