【机器学习】《动手学深度学习》d2l 李沐B站视频配套学习笔记

各种基础铺垫

如何安装d2l包？

pip install d2l

网络差等问题如果无法安装的话，参考此链接。

说明：d2l是课程工具包，是为这门课配套的一些些好的方法，目的是方便读者能够直快速学习到核心的知识，而不必要在一些例如绘图等地方浪费代码复线的时间，直接复用代码就可以了。

那如何查询d2l中某个方法实现了哪些功能呢？
很简单，去它的github源码（可能需要科学上网）上查就可以了，或者通过代码编辑工具，使用ctrl（苹果用command) + 鼠标左键点击方法即可进入电脑内安装好的源码处查看。
这里举两个例子:

set_figsize是作者自己自定义的方法
而d2l.plt.scatter就是作者调用其他包的方法了

作者在头文件中有引入，是外部的matplotlib工具包里的方法，因此需要百度查询pyplot.scatter()就可以了，不用从d2l源码中找了，因为d2l本身调用的也是外部的工具，同时我们可以知道像这种常用的外部包，d2l在引入时保证了命名的一致性，因此可以根据经验推断方法的功能。

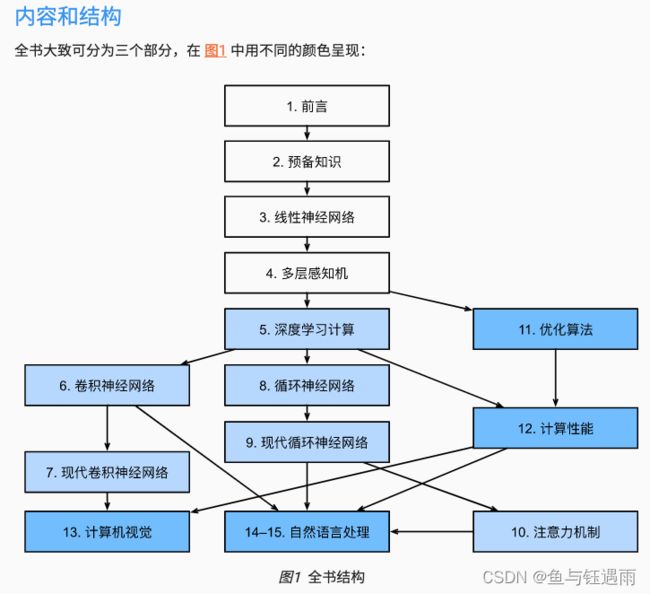
本书的内容框架

3-线性神经网络（基础回归模型）

3.1 内容介绍

当我们想预测一个数值时，就会涉及到回归问题。 但不是所有的预测都是回归问题。 在后面的章节中，我们将介绍分类问题。分类问题的目标是预测数据属于一组类别中的哪一个。

线性回归基于几个简单的假设： 首先，假设自变量和因变量之间的关系是线性的(因此我们会通过散点图来进行初步删选或者取对数）， 即可以表示为中元素的加权和，这里通常允许包含观测值的一些噪声； 其次，我们假设任何噪声都比较正常，如噪声遵循正态分布。

线性假设是指目标（房屋价格）可以表示为特征（面积和房龄）的加权和，如下面的式子：

在开始寻找最好的模型参数（model parameters）和之前， 我们还需要两个东西： （1）一种模型质量的度量方式；——损失函数：平方差损失 （2）一种能够更新模型以提高模型预测质量的方法。——随机梯度下降

由于平方误差函数中的二次方项， 估计值和观测值之间较大的差异将导致更大的损失。 为了度量模型在整个数据集上的质量，我们需计算在训练集个样本上的损失均值，总损失/n（样本数）。

从线性回归到深度网络
到目前为止，我们只谈论了线性模型。 尽管神经网络涵盖了更多更为丰富的模型，我们依然可以用描述神经网络的方式来描述线性模型， 从而把线性模型看作一个神经网络。 首先，我们用“层”符号来重写这个模型。

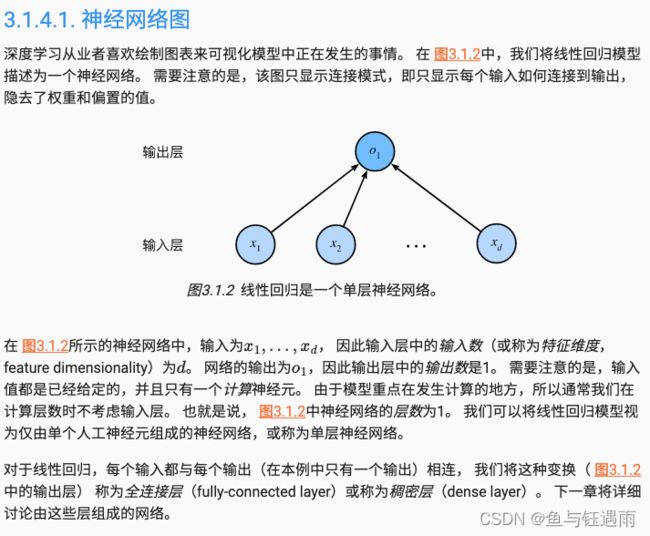
因此，我们可以用一个感知机（没有激活函数）来表示一个线性回归模型。

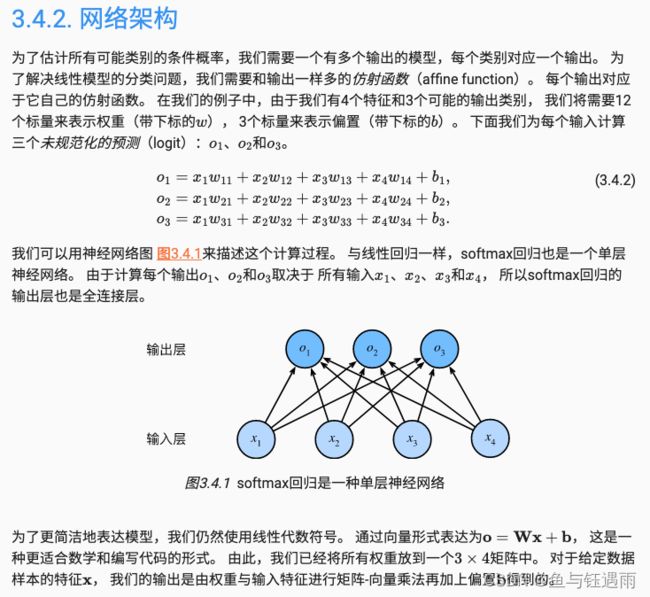
3.4 softmax回归

使用交叉熵损失。

softmax运算获取一个向量并将其映射为概率。

softmax回归适用于分类问题，它使用了softmax运算中输出类别的概率分布。

交叉熵是一个衡量两个概率分布之间差异的很好的度量，它测量给定模型编码数据所需的比特数。

对于分类问题，最基本的模型评估指标是使用精度（accuracy）来评估模型的性能。 （而线性回归问题用loss)

补充：逻辑回归

逻辑回归是将线性回归的值映射到了sigmoid函数当中，它是分类问题，不是回归问题。
是广义的线性回归。

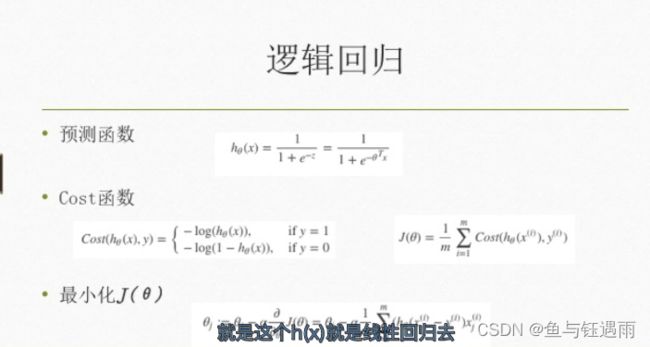
1 线性回归模型完整代码

首先，我们需要定义并背过机器学习代码的流程口诀：定、数、模、训、测、上。（即：问题定义、数据准备、模型搭建、模型训练、模型测试、模型上线。）
针对下面代码所对应的流程：

• 问题定义（回归问题，数据通过函数自己生成 ）
• 模型准备（小口诀：模型、损失、优化器；）
• 模型训练（小口诀： 迭代、调参、降损失；）
• 模型测试
• 模型上线（学术上一般不需要这一步，测试出结果指标，说明模型好就行）

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l
#'nn'是神经网络的缩写
from torch import nn
# 1.数据准备
true_w=torch.tensor([2,-3.4])  ##初始化w
true_b=4.2 ##初始化b
features,labels=d2l.synthetic_data(true_w,true_b,1000)
def load_array(data_arrays,batch_size,is_train=True):
    """构造一个PyTorch数据迭代器"""
    # 实例化一个TensorDataset对象，这个对象可以根据索引返回特征，也可以返回样本数
    dataset=data.TensorDataset(*data_arrays)   #参数是指针类型，指向(features,labels)
    return data.DataLoader(dataset,batch_size,shuffle=is_train)  

#每次挑选batch_size个样本出来
batch_size=10
data_iter=load_array((features,labels),batch_size)    #(features,labels)元祖类型tuple
# print(next(iter(data_iter)))  #iter迭代器，next是成组输出

# 2.构建模型
"""初始化模型参数"""
net=nn.Sequential(nn.Linear(2,1))     #Sequential容器可放多个参数(多层)  y=[1000,2]*[2,1]+[1]=[1000,1]，即为w的形状
net[0].weight.data.normal_(0,0.01)    #net[0]指的是第0层，即nn.Linear(2,1)---w，下划线指使用正态分布来代换掉data的值
net[0].bias.data.fill_(0)             #b
loss=nn.MSELoss()                     #使用均方误差
"""实例化SGD,定义优化算法"""
trainer=torch.optim.SGD(net.parameters(),lr=0.03)

# 3.训练模型
num_epochs=3      #迭代3个周期
for epoch in range(num_epochs):
    for X,y in data_iter:
        l = loss(net(X),y)    #net(X)生成预测并计算损失l(向前传播)
        trainer.zero_grad()   ##trainer优化器梯度清零
        l.backward()          #无需再求sum,pytorch已经计算
        trainer.step()        #调用step进行模型的更新
    """以上是训练过程的loss,放入整个features做损失"""
    l = loss(net(features), labels)
    print(f'epoch: {epoch + 1},loss: {l:f}')

# 4.模型测试（这里的测试并不规范）
w=net[0].weight.data
print('w的估计误差：',true_w-w.reshape(true_w.shape))
b=net[0].bias.data
print('b的估计误差：',true_b-b)

打印结果：
epoch: 1, loss: 0.000213
epoch: 2, loss: 0.000098
epoch: 3, loss: 0.000099
w的估计误差： tensor([-0.0005, -0.0009])
b的估计误差： tensor([0.0001])

2代码拆解-数据准备（数）

from d2l import torch as d2l

代码从d2l包中引入了torch类，并命名为d2l，下面的链接可以看到d2l.torch的详细内容:
官方的d2l.torch.py内容github链接如下：可能需要科学上网

从下图可以看出,d2l中共有如下三个文件，因此from d2l import torch的意思是引入Pytorch版本的d2l工具包，后面加上as d2l是给工具包命名为d2l。可能有点绕，可以这样理解，d2l是一个工具包，但是它有很多版本，为了区分则根据深度学习框架起了名字如下图三个，因此当我们要用d2l这个工具包的时候，需要根据我们使用的深度学习框架来导入版本，然后再重命名为一下，这里我们使用的深度学习框架是Pytorch。

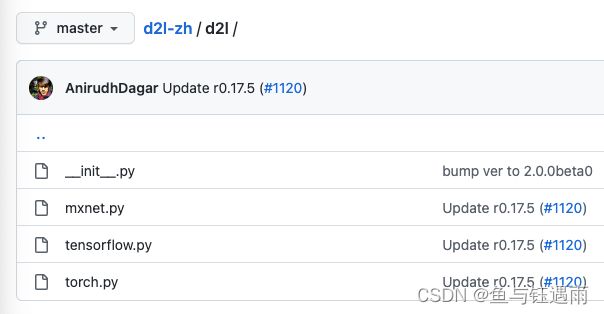
d2l工具包中包含了许多方法；其中一个就是synthetic_data,在pycharm编辑器中，通过ctrl+鼠标左键(mac: command+鼠标左键）的方式就可以进入到该方法的详细内容如下：

reshape = lambda x, *args, **kwargs: x.reshape(*args, **kwargs)

我们可以看到，这个方法其实就是，根据你输入的w，b，以及样本数目，来生成数据。因此洗面这段代码就不难理解了，输入$w=\left[\begin{array}{c}2\\ -3.4\end{array}\right]$,$b=4.2$，随机生成一个样本的特征矩阵$X_{1000\times 2}$，并利用公式$y=Xw+b$进一步生成标签向量y。

# 1.数据准备
true_w=torch.tensor([2,-3.4])  ##初始化w
true_b=4.2 ##初始化b
features,labels=d2l.synthetic_data(true_w,true_b,1000)

3代码拆解-模型准备

"""初始化模型参数"""
net=nn.Sequential(nn.Linear(2,1))     #Sequential容器可放多个参数(多层)  y=[1000,2]*[2,1]+[1]=[1000,1]，即为w的形状
net[0].weight.data.normal_(0,0.01)    #net[0]指的是第0层，即nn.Linear(2,1)---w，下划线指使用正态分布来代换掉data的值
net[0].bias.data.fill_(0)             #b
loss=nn.MSELoss()                     #使用均方误差
"""实例化SGD,定义优化算法"""
trainer=torch.optim.SGD(net.parameters(),lr=0.03)

构建模型步骤：

1. 通过Sequential的方式构建模型
2. 然后对模型中的参数初始化
3. 设定目标损失函数

4代码拆解-模型训练

通俗解释梯度下降参考资料：https://zhuanlan.zhihu.com/p/137374150
l.backward()和optimizer.step()解释参考资料：https://zhuanlan.zhihu.com/p/258084887

# 3.训练模型
num_epochs=3      #迭代3个周期
for epoch in range(num_epochs):
    for X,y in data_iter:
        l = loss(net(X),y)    #net(X)生成预测并计算损失l(向前传播)
        trainer.zero_grad()   ##trainer优化器梯度清零
        l.backward()          #无需再求sum,pytorch已经计算
        trainer.step()        #调用step进行模型的更新
    """以上是训练过程的loss,放入整个features做损失"""
    l = loss(net(features), labels)
    print(f'epoch: {epoch + 1},loss: {l:f}')

在PyTorch里面，loss function 的定义都有一个 reduction 的参数，默认是 mean，也就是平均。
可以选择：
sum： 求和；
none：不做任何操作，直接按位返回所有的值；

# 比如：
loss = nn.MSELoss(reduction='sum') # 'mean' or 'none'

对于任意一个定义好的模型（网络）我们需在模型的输出和标签之间建立一个衡量模型好坏的函数，并且这个函数就是目标函数（损失函数），而所谓的训练就是最小化这个损失函数。损失函数的损失值被优化地越来越小，也就代表其背后的模型精度越来越高，总结起来就是，对于定义好的任意一个模型，我们都需要通过某种方法将其对应的目标函数（损失函数）最小化。

那如何最小化目标函数，在最优化这一门课中，有很多的方法，其中最经典的是随机梯度下降算法。通过该方法，经过对目标函数中包含的模型参数进行求偏导，可以优化调整模型中的权重参数。

l.backward()就是用来执行求解梯度的过程的
trainer.step()就是通过各种不同的优化算法来更新损失函数中（也是模型中）的权重参数的

trainer.step()在参数迭代的时候是如何知道batch_size的？
因为loss = nn.MSELoss()，均方误差是对样本总量平均过得到的，所以trainer.step()使用的是平均过的grad。

在每次l.backward()前都要trainer.zero_grad()，方式l.backward()计算参数梯度的时候，梯度会累加（累加上一个循环的梯度结果）。

4 多层感知机

4.1 感知机-1960年发明

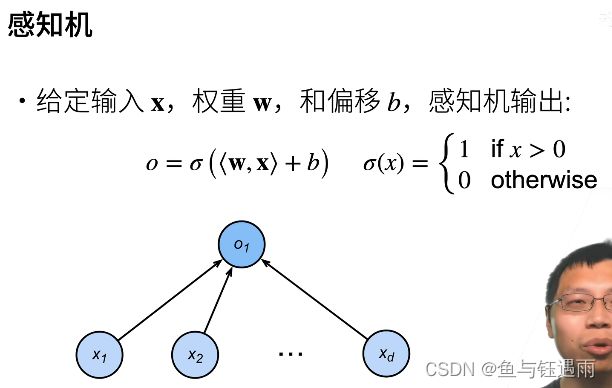
什么是感知机？它为什么一定能收敛？

4.1 感知机

感知机：就是将输入和权重点积之后，再加上权重的结果，再做一个sigma函数，它有多种选择。
。

L2 norm ：L2范数
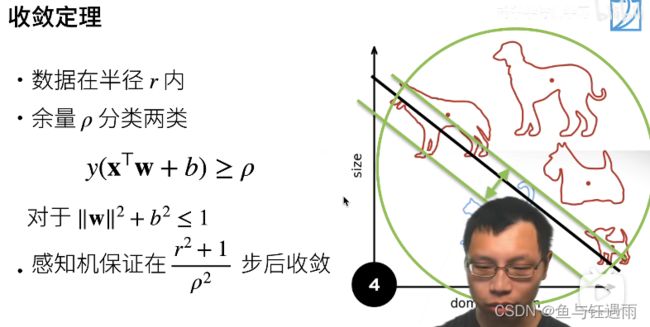
上述感知机的收敛定理是什么样子的呢？ （收敛定理指的是：我的算法更新参数什么时候能够停，是不是真的能够停下）

感知机的收敛定理（不讲证明，10行公式左右）：

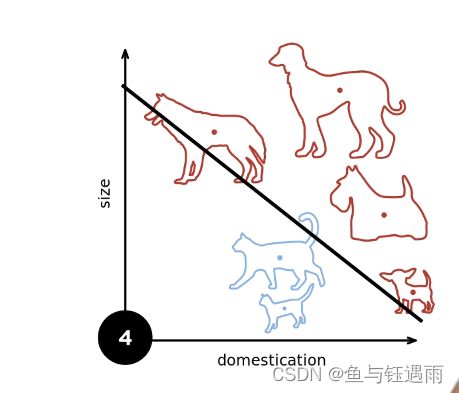
1. 假设我的数据在半径为r的区域里面，
2. 假设我有一个余量$\rho >0$,使得我存在一个分界面，它的权重的L2 norm加起来是小于等于1的，使得我这个分界面能够对所有的分类都是正确的，即$y(x^T+b)$都大于零，而且是有一定余量的，也就是上图中绿色箭头表示的那两个分类面。即我存在一个margin（间距）$\rho$使得我能够将样本全部都分开。
3. 在上述两个假设条件下，感知机确信我们能够找到最优解，并且在$\frac{r^2+1}{\rho }$步后收敛（就是停止)。
   通俗理解，r就是你的数据的范围大小，当它很大的时候，你就会收敛地很慢。$\rho$可以用来判断你的数据是不是很好，如果分割面特别地小，那么我们找能够正确分类所有样本的分割面就会花更多的时间。

感知机存在的问题？

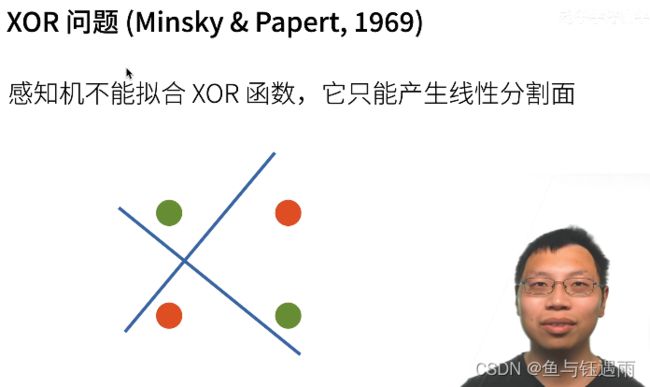
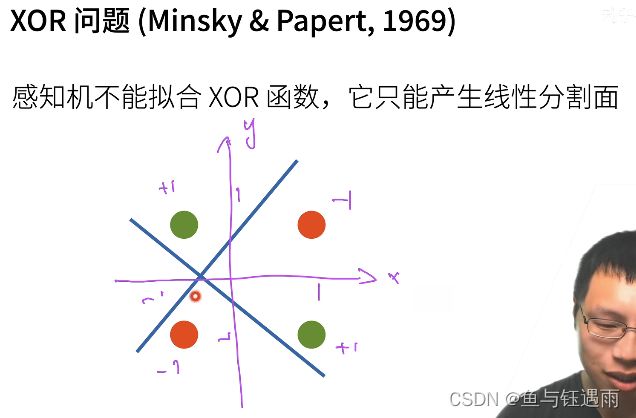
XOR（异或问题）是说，当我在紫色坐标系中输入的x和y都是1的时候，是-1类，坐标符号不同的时候是1类。
那上面我们说了，感知机对于二维的输入，由于它是一个线性模型，那么它的分割面一定是一道线。我们可以看到，无论如何画线，都不能够把数据给分类对。

线性，模型定义如下：

因此感知机不能拟合简单的XOR的函数。因为感知机只能产生线性分隔面。这是Minsky在1969年提出的，你们的感知的什么时候不work的问题。这个问题直接导致了AI的第一个寒冬，如此复杂的模型，连一个简单的XOR函数都你不出来，导致大家都去转行了。

等到10-15年之后，大家发现通过多层感知机可以解决这一个问题。

感知机总结

4.2 多层感知机

多层感知机-单分类（二分类）

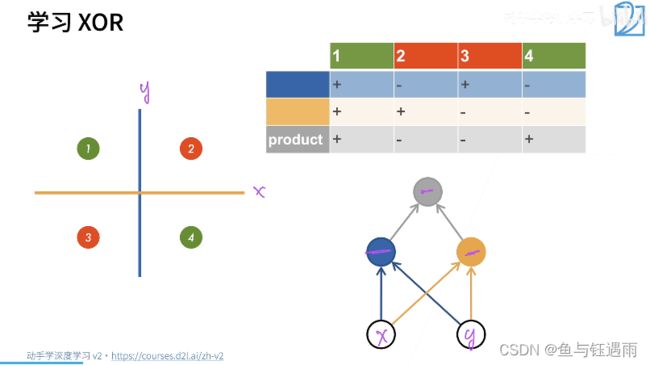
假设我们一次你和不了，那我们就先学一个简单函数(分类器)，再学另外一个简单函数（分类器），最后将两个函数的结果组合起来，这样就从1层感知机变成了多层感知机。

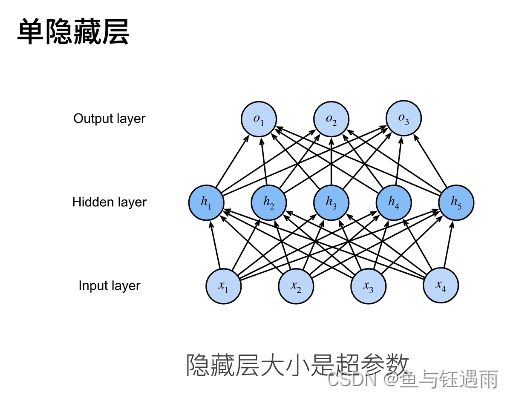
多层感知机输入和输出的大小分别是由数据和问题决定的。

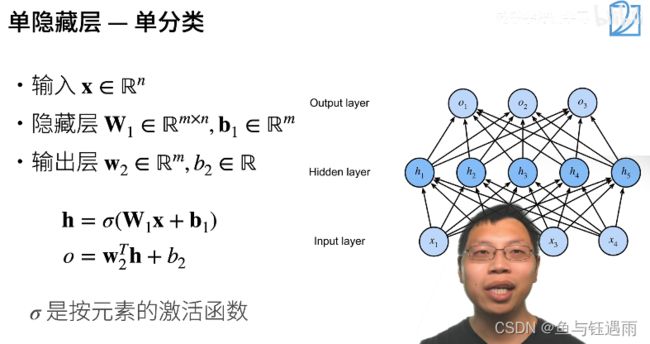
$R^m$是一个长为m的向量。
那为什么需要一个非线性的激活函数呢？

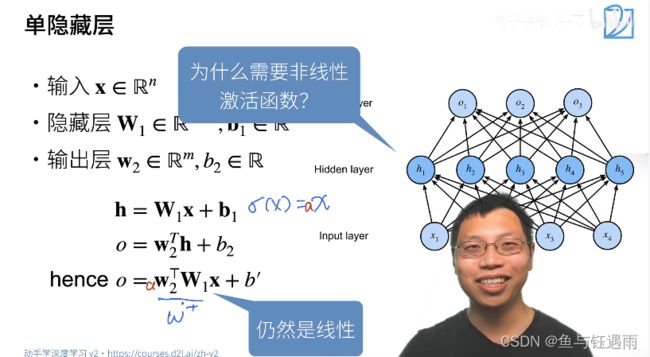
因为如果你不加非线性激活函数，你多层感知机实际得到的模型仍然是一个线性模型，不能解决XOR问题。

常用的激活函数-没有太多想法就用Relu

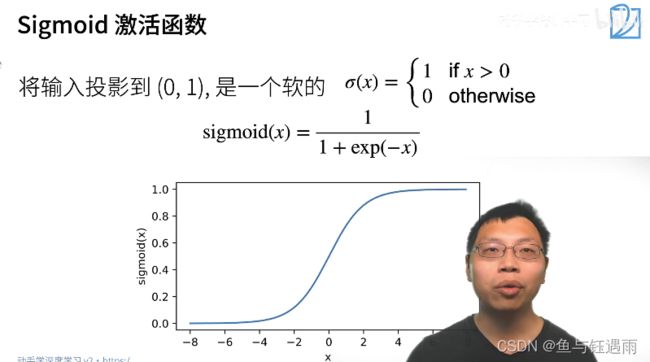
个人备注：sigmoid还有一个优点是输出范围为(0, 1)，所以可以用作输出层，输出表示概率。


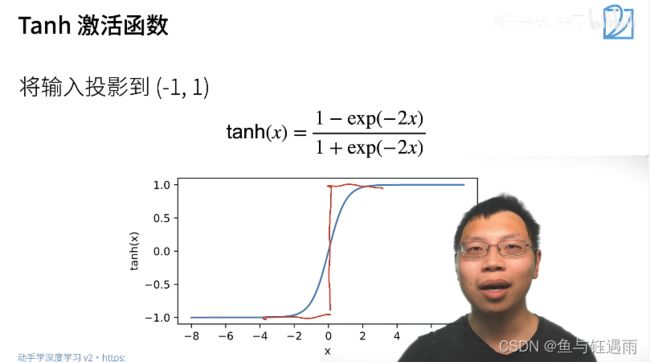
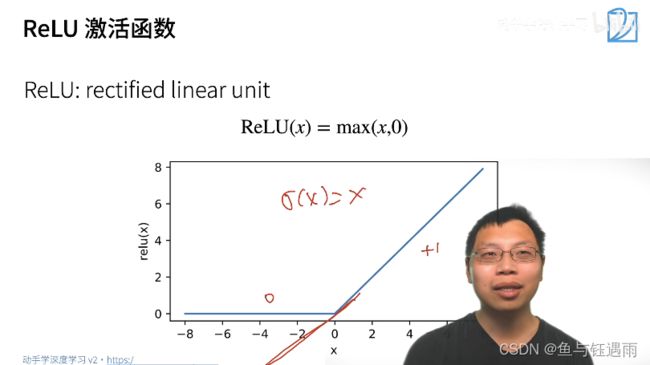
Relu常用的原因：主要原因是比指数计算快很多，很简单。

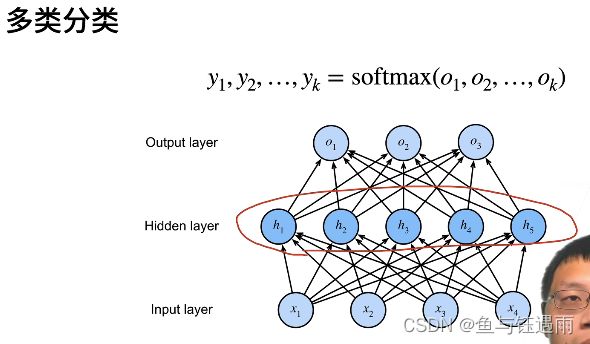
多层感知机（多分类）

多层感知机的多类分类和softmax回归没有本质区别的原因在于，多层感知机分类唯一加的就是中间层，如果没有的话，就是最简单的softmax回归。加了一层，就是多层感知机了。

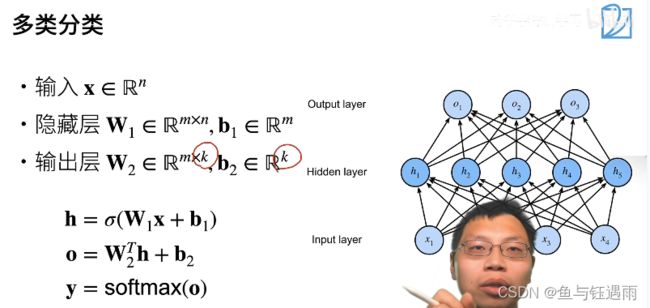
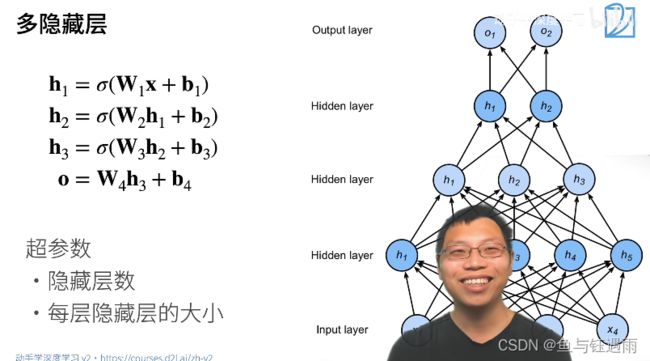
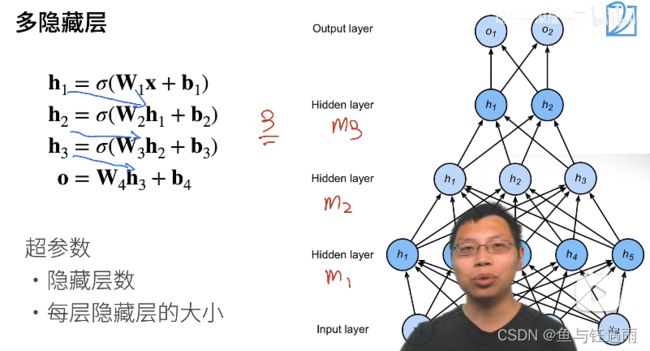
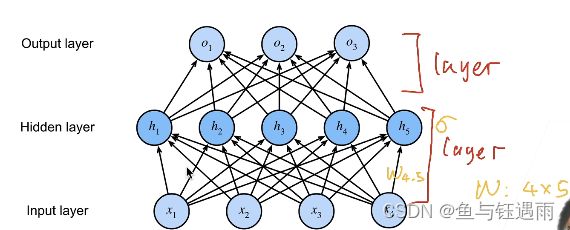
多层感知机超参数设定（隐藏层>1型)

每一层隐藏层都有它自己的w和偏移b,以及一个激活函数。
注意，激活函数不能少，少了就相当于层数减1了。另外输出层是不需要激活函数的。激活函数主要是为了防止我们曾数的塌陷，最后一层不用激活函数。
多层感知机和多隐藏层(>1)感知机之间的区别就是，我们的超参数又多了一个：隐藏层数，之前只有隐藏层大小。
☀️
其中：对隐藏层数和每层隐藏层的大小我们通过经验性的配置来设定，通常将最底层，如图的m1层设置的稍微大一点点。
简答解释如下：
假设我的数据比较复杂，不考虑线性模型的情况下 ，我想用多层感知机，那么我就有两个选择，把模型做大和把模型做深。

1. 把模型做大 ：那就单隐藏层来讲，m1设定地大一点点，假设我们的输入维度是128，那我们的隐藏层设置为64、128、256都行。
2. 把模型做深：如果我用多隐藏层，例如3个，那么我的m1通常要设定地比单隐藏层小一点,m2和m3也依次减小。

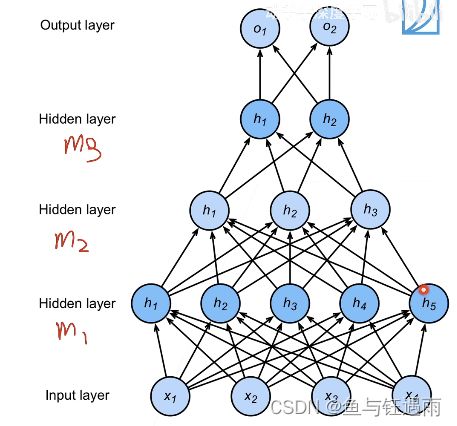
那为什么向上面这样设定呢？假设你的数据比较复杂，那么通常来说你的维度是比较高的（128或者256，这就比较高了），那么你的输出往往相对来说是比较少的，例如10类或者5类，或者1类，那你从128压缩到1，你最好是满满地把这些数据压缩过去，最简答的操作就是128->64->32->16->8->输出5，不断地提取，同时，一般来说，我们把最前面的一层可以胖一点，但一定不能太小，这样会丢失很多信息,后面再还原是比较难的。
而在我们讲的CNN的时候，我们有时候会把模型先压缩，再扩张，以此来避免模型overfitting（过拟合，后面会讲），也就是说对于不同的模型方法，超参数的设定往往是不同的，而且绝大多数是通过经验来设定的，没有太多的道理。

多层感知机总结

4.3 多层感知机代码实现

3.6 softmax回归从0实现

4.2 多层感知机MLP从0实现

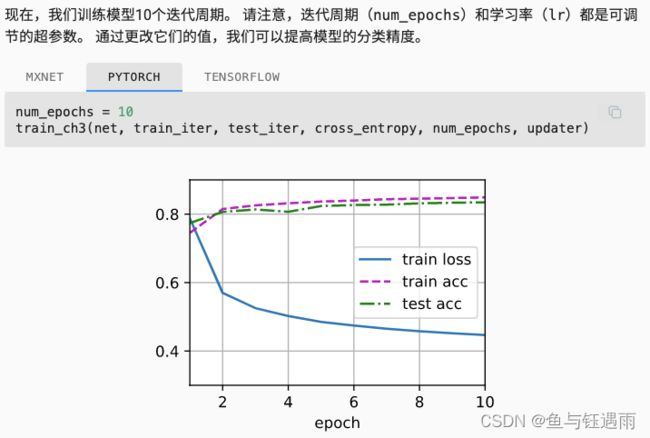
由于我们的模型更大了（参数更多了），所以对数据的拟合性更好，所以参数下降了。

多层感知机简洁实现

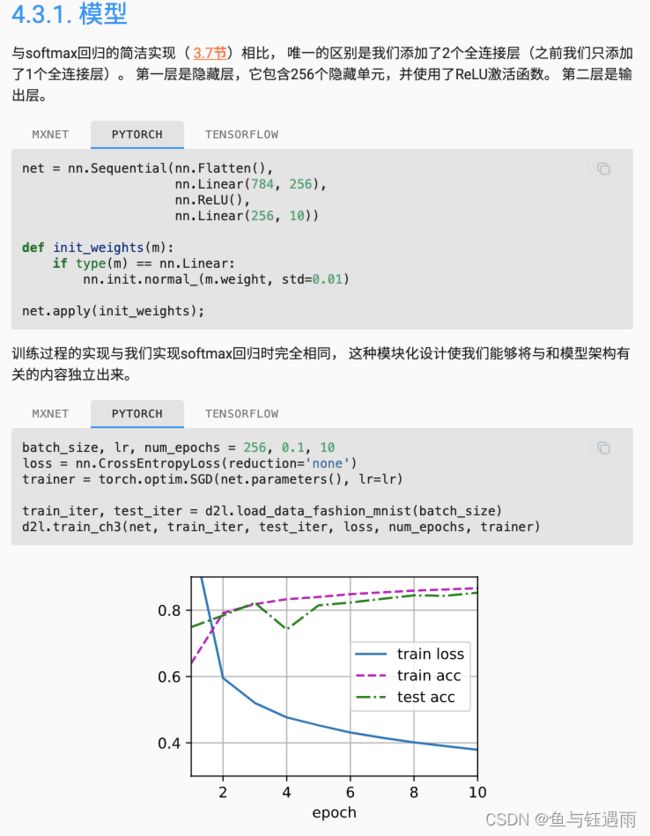
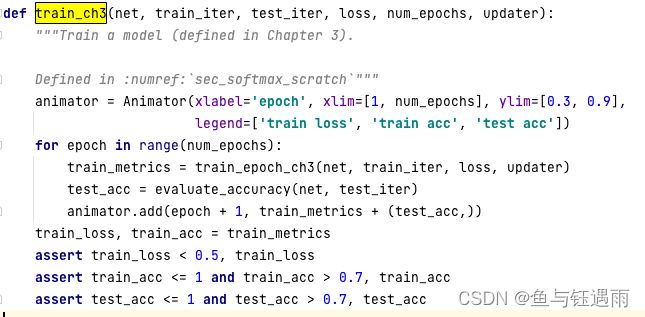
我们可以看到，我们模型变化很大，但是从代码实现角度来讲只改了一点点。这也是我们为什么不用SVM的原因，因为SVM虽然可能更容易调，也更简单。但是当MLP不起作用的时候，我们可以很容易地转向卷积CNN，RNN或者Transformer。而SVM可能要调的东西就会多很多。

4.4 多层感知机答疑

1. 到底多层感知机中的一层指的是什么？
   一般来说，权重w和一个激活函数组合为一层（注意输出层不需要激活函数，输入层我们不作为一层），那这里就是一个二层的感知机。（当然了，还有别的理解方法，但是W有几层，就是几层，这是关键）

2. 老师，数据的区域R怎么测量，或者统计？rou怎么设定？实际中我们确实想找到数据分布的区域，可以找到吗？
其实，从统计的角度来讲，rou是我们定义出来的东西。是数学统计中的内容，是证明收敛的内容，不能用来指导实际的生产。（因此我们知道即可，不用深究，做深度学习，或者说偏计算的机器学习，不考虑这些统计的问题）
2. 在当时，SVM比多层感知机流行的原因是什么？
SVM是上个世纪90年代出来的，1990年左右。而感知机是1970年左右感知机就进入冬天了，到SVM出现之间其实还有几十年，多层感知机在这之间就产生了。
可以说多层感知机解决了感知机XOR的问题，但是之后没有流行是因为两个问题，第一，你得学超参数，你得学多个隐藏层，每个隐藏层多大，这个都是”老中医“靠经验的东西，而且收敛也不好收敛，需要调各种学习率。而SVM的好处是说，他没有那么多的超参数可以学，它对超参数不敏感，比如说基于Kernal核的SVM，它的Kernal调宽一点或者调窄一点都没关系。第二，SVM的优化接起来会比较容易一点点，不需要SGD。第三个，对于学术界来讲，如果SVM和多层感知机效果差不多，那由于SVM有很漂亮的数学理论，所以会更追求有数学性的东西。
综上，SVM从上世纪90年代一直到2000年，一直是我们机器学习的主流，因为数学很好，而且效果也不差。 现在我们建议用MLP的最大原因，是因为简单，变化升级起来容易。
3. 多层感知机能够干什么？
多层感知机，我们能够证明只要有一个隐藏层，你是可以拟合一个任意函数。就是一层感知机，理论上我们能够拟合整个世界，但实际上做不到，因为优化算法解不出来，这是实际的问题。
4. 神经网络为什么要增加隐藏层的层数，而不是神经元的个数？ 不是有神经网络万有近似性质吗？
多层感知机的实现方式，有下面两种方式，他们的复杂度理论上相等。
但是从训练的角度上讲，左侧的模型不好训练，右侧的模型好训练，右侧的模型叫深度学习，左侧矮胖的模型叫浅度学习。

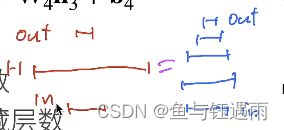
那为什么呢？ 对于左侧的模型：首先，因为左侧的模型容易过拟合，其次，所有的神经元参数一起并行计算解决问题，从直觉上来讲合作起来解决问题就很难；最后，一下子解决问题和一点点解决问题明显前一个难度大。
对于右侧的模型：每一层学一点点东西，最后学出来的比较好。（但是这没有理论依据，是人的直观感觉）
个人总结：因此当模型是一个线性可分问题是，我们直接用感知机即可，但是多层感知机可以同时解决线性可分和线性不可分问题，因此当不去证明的时候，直接用多层感知机就行。理论上一层隐藏层的多层感知机就可以解决所有问题，但是，当初始特征很大的时候，单隐藏层多层感知机的隐藏层的神经元个数往往很大，很难学习，因此当特征超过64的时候，我们通常就需要多层感知机的。而多层感知机每一层怎么设置的经验？参考4.2节中 多层感知机超参数 的设定。
5. 老师Relu为什么管用？它在大于0的部分也就只是线性变换，为什么能促进学习呢？激活的本质是要做什么事？
Relu管用就是因为引入了非线性，可以拟合任意函数。激活的本质就是引入非线性（而Rule是分段线性函数，不属于线性函数）。
5. 不同任务下激活函数是不是都不一样？ 也是通过实验来确认吗？
其实都差不多，激活函数远远没有选择隐藏层大小和隐藏层层数这种与模型结构相关的超参数来得重要。所以大家尽量就用Relu就行。你可以选，但其实本质上没有太多区别。

6. 老师，模型的深度和宽度哪个更影响性能，有理论指导吗？就是加深哪个更有效。怎么根据输入空间，选择最优的深度或者宽度？
   理论上没有区别，实际上来说深一点的会好一点。
   通常来讲，如果我手里有一个数据，特征是128，二分类问题。第一步，我一般会先做一个没有隐藏层的试一试行不行，跑一下线性的。然后再做一个有隐藏层的试一试，一开始加一个隐藏层，然后不会做很大，比如说16，因为是168到2嘛，然后再逐一增加，当16和128效果不好，32和64效果提升了的话。 第三步，再加一层试试效果。
   当最后一个隐藏层的大小和输出层的维度差不多的时候，就说明可以停止了。
   当然了，可以写一个循环测试，但是没必要，根据经验差不多试试就行。
7. 为什么参数有的人写W有的写W的转制
   这个是都可以的。
8. 动态网络可行吗？
   有随机性的预测不可行，会出问题，比如说把张地像金丝猴的人预测成金丝猴。
9. 泛化性（鲁棒性）
   指的是，来了新的数据，我们的预测结果很稳定。（在医疗和交通领域很重要）

4.5 多层感知机个人经验大总结

参考国外高赞经验贴文章：multi-layer perceptron (MLP) architecture: criteria for choosing number of hidden layers and size of the hidden layer? [closed] (选择隐藏层尺寸和隐藏层数量的标准）

我们知道，感知机（没有隐藏层）可以处理线性可分的数据（4.1有解释，不用管记住就行），因此除非你已经知道你的数据不是线性可分的，就用感知机就行。所以，验证数据的线性可分性这一点并没有坏处，因为我们没有必要使用比任务要求更加复杂的模型（多层感知机）来解决简单技术（感知机）就能够解决的线性可分问题。

1. 那如何判断数据是否线性可分呢？如何判断数据是否线性可分
2. 怎样区分线性和非线性_线性与非线性的区别（线性分析、线性模型）

假设你的数据的确需要非线性技术才能够分离，则始终从一个隐藏层开始。毫无疑问，这是你必须做的。如果你的数据可以通过MLP分离，那么MLP大概率只需要一层。这有理论上的理由，但是我们通常纯粹从经验上来解释：许多困难的分类和回归问题，通常使用单隐藏层的多层感知机就能够解决。尽管在一些地方确实存在多层的应用，但是能够证明其合理性的非常少。
**隐藏层中有多少节点? **
来自MLP的学术文献和个人的经验等，我们收集并经常依赖于一些经验法则(RoT：rules of thumb)，也发现它们是可靠的指南（这些指导往往是准确的，即使不准确也能够告诉我们每一步应该干什么）

• 根据输入层和输出层大小的经验法则：

1. 隐藏层的大小介于输入层和输出层之间
2. 计算方式：(输入数量+输出数量）$\times$ 2/3

• 基于主成分

1. 将尽可能多的隐藏层节点数指定为能够捕获输入数据集70%-90%数据差异的主成分的维度。

然而，NN FAQ作者将这些规则称为“胡说八道”（从字面上看），因为它们：忽略训练实例的数量，目标中的噪声（响应变量值）以及特征空间的复杂性。

在他看来，根据您的MLP是否包括某种形式的正则化或早期停止，选择隐藏层中神经元的数量。

在实践中，我这样做：

1. 输入层：我的数据量的大小（我的模型中特征的大小）
2. 输出层：由我的模型确定：回归（一个节点）与分类（假设SoftMax，则节点数量等于分类类数）
3. 隐藏层：开始，一个隐藏层的节点等于输入层的大小。 “理想”的大小可能更小（即，输入层中的数字与输出层中的数字之间的一些节点）而不是较大，是一个经验。如果项目需要额外的时间，那么我就从一个由少量节点组成的单一隐藏层开始，然后（就像我上面解释的那样）我在计算泛化误差、训练误差、偏差和方差的同时，一次一次地向隐藏层添加节点。当泛化误差已经下降，并在它开始再次增加之前，这时的节点数量是我的选择。见下图。
   

排除上面的内容，只有当数据的初始特征很大的时候，我们才考虑增加MLP的隐藏层数。

5 深度学习计算-层和块

如何打印展示我们当前模型中的块有什么?

import torch
from torch import nn

net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(), nn.Linear(8, 1))
X = torch.rand(size=(2, 4))
print(net(X))

tensor([[0.1713],
[0.1713]], grad_fn=AddmmBackward0)

print(net)

Sequential(
(0): Linear(in_features=4, out_features=8, bias=True)
(1): ReLU()
(2): Linear(in_features=8, out_features=1, bias=True)
)
我们可以看到,整个模型,有2个块,很清晰. 注意,有时候,一个块里会有很多层.

from torchsummary import summary
# 如果没有torchsummary这个包,安装一下
#安装命令: pip install torchsummary
summary(net,input_size=(2,4))

效果如下,input_size指的是你给定一个输入的维度. 这里的2,4代表两个样本,每个样本的特征长度是4.

----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Linear-1                 [-1, 2, 8]              40
              ReLU-2                 [-1, 2, 8]               0
            Linear-3                 [-1, 2, 1]               9
================================================================
Total params: 49
Trainable params: 49
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.00
Params size (MB): 0.00
Estimated Total Size (MB): 0.00
----------------------------------------------------------------