递归+递推 DFS+回溯+剪枝

递归+递推

递归

递归可以理解为自上而下，生成一棵递归搜索树，把某一个问题分解成若干个同种子问题。

递归求斐波拉契数

公元 1202 年，意大利数学家莱昂纳多·斐波那契提出了具备以下特征的数列：
前两个数的值分别为 0 、1 或者 1、1；
从第 3 个数字开始，它的值是前两个数字的和；
为了纪念他，人们将满足以上两个特征的数列称为斐波那契数列。

如下就是一个斐波那契数列：
1 1 2 3 5 8 13 21 34......

下面是代码：

#include

using namespace std;

int dfs(int u)
{
	if(u==1) return 1;
	if(u==2) return 1;
	return dfs(u-1) + dfs(u-2);
}

int main()
{
	int n;
	cin >> n;
	cout << dfs(n) <<endl;
	return 0;
}

递归实现指数型枚举

从 1∼n 这 n 个整数中随机选取任意多个，输出所有可能的选择方案。

输入格式
输入一个整数 n。

输出格式
每行输出一种方案。

同一行内的数必须升序排列，相邻两个数用恰好 1 个空格隔开。

对于没有选任何数的方案，输出空行。

本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

数据范围
1≤n≤15
输入样例：
3
输出样例：

3
2
2 3
1
1 3
1 2
1 2 3

什么是指数型枚举?

	每个数都有【选与不选】两种选择，即共有2的n次幂种选择

该题在考什么算法？

————分析题目可知，我们大致看来，每个数字被选与否会影响方案的不同，所以，不选与被选的相互影响可以看作是递归问题，用dfs算法来求解。

所以，这是个递归问题，而所有的递归问题都可以转换成一棵递归搜索树的dfs问题。

大致思路：从1到n依次考虑每个数选不选，
下面我们来看一下图解：

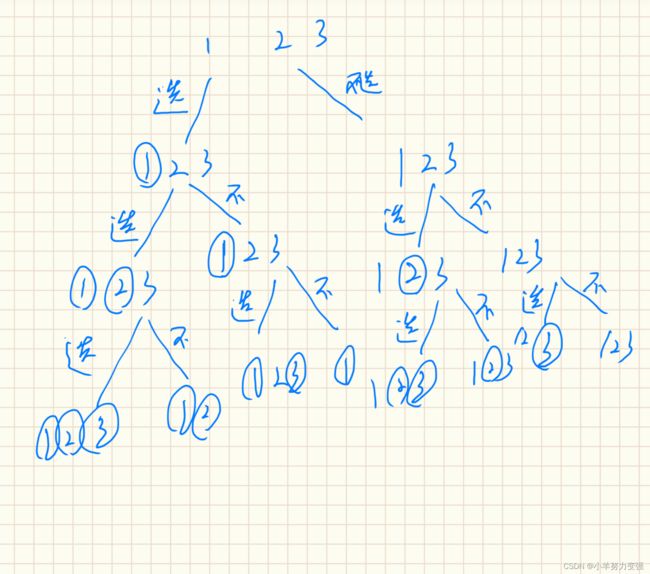
圆圈圈出的数表示选了，没圈的就表示没选。

接下来请看以下代码：

#include

using namespace std;

const int N = 16;

int n;
bool used[N];

void dfs(int u)
{
    if(u > n) //边界问题
    {
        for(int i = 1 ; i <= n ; i ++)
        {
            if(used[i])  //如果这个数被选了就输出
            {
                cout << i << " ";
            }
        }
        cout << endl;
        return ;
        
    }
    else 
    {
        used[u] = true;   //选这个数
        dfs(u + 1);
        
        used[u] = false;  //不选这个数
        dfs(u + 1);
    }
}

int main()
{
    cin >> n;
    dfs(1);
    return 0;
}

这里和题输出的不一样是因为题先都不选，不过没关系，因为本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

dfs(1)
{
	used[1]=true //选1
	dfs(2)
	{
		used[2]=true //选2
		dfs(3)
		{
			used[3]=true //选3
			dfs(4)
			{
				(4>3)
				{
					for(i->n)输出i
					if(used[i]==true)
					输出1 2 3
				}
				换行
			}
		}
	}
}

递归实现排列型枚举

把 1∼n 这 n 个整数排成一行后随机打乱顺序，输出所有可能的次序。

输入格式
一个整数 n。

输出格式
按照从小到大的顺序输出所有方案，每行 1 个。

首先，同一行相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面。

数据范围
1≤n≤9
输入样例：
3
输出样例：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

什么是排列型枚举？

——【位置】和【数字】之间是有顺序的。eg：123和132是不同的方案

这题可以直接用STL中的next_permutation求解，不过时间复杂度
由数学方法可知：全排列共有N!种即N!此循环，即时间复杂度约为N!

我们还是递归求解先画图，画出递归搜索树：

接下来请看代码：

#include

using namespace std;

const int N = 10;

int n;
int st[N]; // 0 表示还没放数，1~n表示放了哪个数
bool used[N]; // true表示用过，false表示还未用过

void dfs(int u)
{
    if(u > n)
    {
        for(int i = 1 ; i <= n ; i ++)
        {
            cout << st[i] << " ";
        }
        cout << endl;
        return ;
    }
    // 依次枚举每个分支，即当前位置可以填哪些数
    for(int i = 1 ; i <= n ; i++)
    {
        if(!used[i])
        {
            st[u] = i;
            used[i] = true;
            dfs(u+1);
            
            //回溯
            st[u] = 0;
            used[i] = false;
            
        }
    }
}

int main()
{
    cin >> n ;
    dfs(1);
    return 0;
}

dfs(1)
{
	for()
	{
		st[1]=1;
		used[1]=true
		-------------以下是dfs(u+1)的内容-------------
		dfs(2)
		{
			st[2]=2
			used[2]=true
			dfs(3)
			{
				st[3]=3;
				used[3]=true
				dfs(4)
				(4>3)
				{
					输出st[];
				}
				换行
			}
		}
		-------------以上是dfs(u+1)的内容-------------
		//回溯，不然下次循环无法进行，将下面代码注释后将只输出一行1 2 3 
		st[u] = 0;
        used[i] = false;
	}
}

这里再附上用STL求解的代码：

#include 

using namespace std;

int n, a[10];

int main() {
    cin >> n;
    for (int i = 0; i < n; i++)
        a[i] = i + 1;
    do {
        for (int i = 0; i < n; i++)
            cout << a[i] << ' ';
        cout << endl;
    } while (next_permutation(a, a + n));
    return 0;
}

递归实现组合型枚举

从 1∼n 这 n 个整数中随机选出 m 个，输出所有可能的选择方案。

输入格式
两个整数 n,m ,在同一行用空格隔开。

输出格式
按照从小到大的顺序输出所有方案，每行 1 个。

首先，同一行内的数升序排列，相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面（例如 1 3 5 7 排在 1 3 6 8 前面）。

数据范围
n>0 ,
0≤m≤n ,
n+(n−m)≤25
输入样例：
5 3
输出样例：
1 2 3 
1 2 4 
1 2 5 
1 3 4 
1 3 5 
1 4 5 
2 3 4 
2 3 5 
2 4 5 
3 4 5 

什么是组合型枚举？和排列型枚举代码上有何联系？如何去由排列型枚举转变成组合型枚举呢？

————不考虑顺序的枚举，是组合型枚举，eg：123和213是一种方案；而在排列型枚举中是属于不同方案

————限制后面位置要放的数字比前一个位置要放的数字大，就可以满足不重复，实现去重

还是同样的，我们先来看图解，从1、2、3、4、5中选3个数，选的时候我们就可以从小开始，就可以保证是字典序排序，并且不需要去重。

接着来看代码：

#include

using namespace std;

const int N = 30;

int n, m;
int way[N];

void dfs(int u, int start)
{
    if (u == m + 1)
    {
        for (int i = 1; i <= m; i ++ ) 
            printf("%d ", way[i]);
        printf("\n");
        return;
    }

    for (int i = start; i <= n; i ++ )
    {
        way[u] = i;
        dfs(u + 1, i + 1);
        way[u] = 0; // 回溯，可以不用，因为会被自动覆盖
    }
}

int main()
{
    scanf("%d%d", &n, &m);

    dfs(1, 1);

    return 0;
}

保持升序, 是一个局部的属性, 只要保证每次新加的数大于前一个数
a1n)
		way[1]=1
		dfs(2,2)
		{
			for(2->n)
				way[2]=2
				dfs(3,3)
				{
					way[3]=3
					dfs(4,4)
					(4>3)
					{
						for(i->m)
						输出way[i]
					}
					换行
				}
				dfs(3,4)
				way[3]=4;//这里可以不用回溯，因为会被自动覆盖
				dfs(4,4)
					(4>3)
					{
						for(i->m)
						输出way[i]
					}
					换行
		}
}

其实我们还可以把这个代码优化，也就是剪枝
怎么剪枝呢？
我们可以知道，4/5这两个分支根本就不需要递归，所以我们在前面就一个判断

if (u + n - start < m) return;     // 剪枝

全部代码就是

#include

using namespace std;

const int N = 30;

int n, m;
int way[N];

void dfs(int u, int start)
{
	if (u + n - start < m) return;     // 剪枝
    if (u == m + 1)
    {
        for (int i = 1; i <= m; i ++ ) 
            printf("%d ", way[i]);
        printf("\n");
        return;
    }

    for (int i = start; i <= n; i ++ )
    {
        way[u] = i;
        dfs(u + 1, i + 1);
        way[u] = 0; // 回溯，可以不用，因为会被自动覆盖
    }
}

int main()
{
    scanf("%d%d", &n, &m);

    dfs(1, 1);

    return 0;
}

我们可以来对比一下运行时间

5秒前的就是我剪枝后的代码，10小时前的就是没有剪枝的代码，这个时间快了一倍多。

递推

递推可以理解为自下而上，先求子问题，然后由子问题去推原问题。

简单斐波那契

以下数列 0 1 1 2 3 5 8 13 21 ... 被称为斐波纳契数列。

这个数列从第 3 项开始，每一项都等于前两项之和。

输入一个整数 N，请你输出这个序列的前 N 项。

输入格式
一个整数 N。

输出格式
在一行中输出斐波那契数列的前 N 项，数字之间用空格隔开。

数据范围
0

我们在之前用递归求解这道题的时候是从上一层一层向下求解的，我们先想f(n)怎么做，f(n)=f(n-1)+f(n-2)，这就是递归的写法。那么递推怎么写呢？
先来看代码

#include

using namespace std;

int fb[50];
int main()
{
    int n;
    cin >> n;
    fb[0] = 1;
    cout << fb[1];
    for(int i = 2 ; i <= n ; i++)
    {

        fb[i] = fb[i-1]+fb[i-2];
        cout<<" "<<fb[i];
    }

    return 0;
}

递推式子：f(n) = f(n - 1) + f(n - 2)
初始化一个数组前两项为0、1
根据递推式子从第三行开始递推

然后可以对这代码进行优化：

#include 

using namespace std;

int main()
{
    int a = 0, b = 1;
    int n;
    cin >> n;

    for (int i = 0; i < n; i ++ )
    {
        cout << a << ' ';
        int c = a + b;
        a = b, b = c;
    }

    cout << endl;

    return 0;
}

翻硬币

小明正在玩一个“翻硬币”的游戏。

桌上放着排成一排的若干硬币。我们用 * 表示正面，用 o 表示反面（是小写字母，不是零）。

比如，可能情形是：**oo***oooo

如果同时翻转左边的两个硬币，则变为：oooo***oooo

现在小明的问题是：如果已知了初始状态和要达到的目标状态，每次只能同时翻转相邻的两个硬币,那么对特定的局面，最少要翻动多少次呢？

我们约定：把翻动相邻的两个硬币叫做一步操作。

输入格式
两行等长的字符串，分别表示初始状态和要达到的目标状态。

输出格式
一个整数，表示最小操作步数

数据范围
输入字符串的长度均不超过100。
数据保证答案一定有解。

输入样例1：
**********
o****o****
输出样例1：
5
输入样例2：
*o**o***o***
*o***o**o***
输出样例2：
1

这是第四届蓝桥杯省赛C++B组的一道题，我们来看代码：

#include 

using namespace std;

const int N = 110;

int n;
char start[N], aim[N]; 

void turn(int i)
{
    if (start[i] == '*') start[i] = 'o';
    else start[i] = '*';
}

int main()
{
    cin >> start >> aim; //读入两个字符串
    n = strlen(start);   //读一下两个字符串长度，因为保证有解，所以不用考虑两个字符串是否一样长

    int res = 0;
    for (int i = 0; i < n - 1; i ++ )  //还是保证有解，所以只需要到n-1就可以了
        if (start[i] != aim[i])
        {
            turn(i), turn(i + 1);  //翻转两个相邻的硬币
            res ++ ;
        }

    cout << res << endl;
    return 0;
}

其实这题有点DP的意思了。

最后两道题有一点敷衍了，但现在已经是23：50了，明天早八，如果后面有什么问题的话欢迎留言。