深度学习基础-1

0 前言

本文是公司组内分享的课程笔记，主要参考了北邮鲁鹏老师的《计算机视觉与深度学习》课程，课程视频链接在这里。

这一讲还没有涉及到神经网络相关知识，是以图像分类任务为例，对除了神经网络之外的深度学习知识点概览。目的是讲清楚深度学习的总体流程，同时让读者对深度学习工作者的思考方式有一个了解。

1 图像分类简介

1.1 什么是图像分类

图像分类任务是计算机视觉中最基础也是最核心的一项任务，许多更加复杂的问题都可以转化为图像分类问题，如目标检测可以转化为对ROI(Region of interest)的分类问题，图像分割可以转化为对每个像素点的分类问题。

图像分类的核心是根据图像信息中所反映的不同特征，把不同类别的图像区分开来，即从已知的类别标签集合中为给定的输入图片选定一个类别标签。

图1-1 图像分类任务

1.2 图像分类任务的难点

计算机做图像分类和人对图像分类有挺大的区别，人认为很简单的问题，在计算机看来并不是如此，目前主要的难点包括以下几点：
（1）语义鸿沟

图1-2 语义鸿沟

（2）类别繁多

图1-3 类别繁多

（3）不同视角

图1-4 不同视角

（4）不同光照

图1-5 不同光照

（5）遮挡问题

图1-6 遮挡问题

（6）不同形变

图1-7 不同形变

（7）尺度问题

图1-8 尺度问题

（8）运动模糊

图1-9 运动模糊

1.3 分类任务的评价指标

分类任务的评价指标其实就是在一个叫做混淆矩阵(confusion matrix)的东西上做文章。

针对一个二分类问题，即将实例分成正类（positive）或负类（negative），在实际分类中会出现以下四种情况：

（1）若一个实例是正类，并且被预测为正类，即为真正类TP(True Positive )
（2）若一个实例是正类，但是被预测为负类，即为假负类FN(False Negative )
（3）若一个实例是负类，但是被预测为正类，即为假正类FP(False Positive )
（4）若一个实例是负类，并且被预测为负类，即为真负类TN(True Negative )

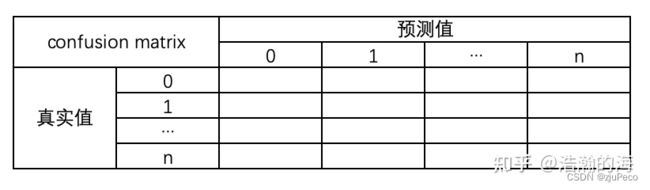
混淆矩阵的每一行是样本的预测分类，每一列是样本的真实分类（反过来也可以），其形式如下图1-2所示。

图1-10 二分类混淆矩阵

对于多分类的问题，混淆矩阵的计算与二分类任务相似，只是类别数由之前的两个变成现在的多个，多分类混淆矩阵形式如下图1-3所示。

图1-11 多分类混淆矩阵

每一个单元格第$i$行，第$j$列表示的是，预测值为$j$，真实值为$i$的个数。

为了更加直观地说明多分类的混淆矩阵，下面给出一个真实的例子，如图1-4所示。

图1-12 多分类混淆矩阵实例

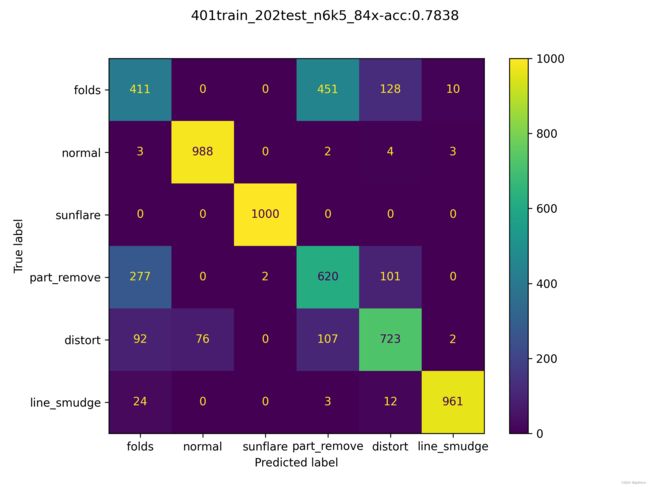
图1-4中共有6个类别，每个类别1000个样本，纵轴表示每个样本的真实标签，横轴表示每个样本的预测标签。对角线的值越大，说明模型的效果越好，比如sunflare这个类别模型的预测准确率是100%的，不会和其他任何一个类别混淆。又比如folds和part_remove就很容易混淆，folds有451个被误认为是part_remove，part_remove有277个被误认为是folds。

通过混淆矩阵，我们可以人为看出模型总体和细粒度的分类能力，不过还是需要有具体的数值指标，比如Accuracy，Precision和Recall。

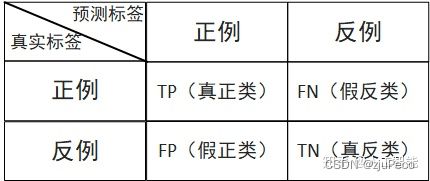
还是以二分类为例，我们重新来看一下混淆矩阵，如下图1-5所示。多分类的时候，可以把其中一个类别当做正例，其他的类别当做反例，转化为二分类的混淆矩阵。

图1-13 二分类混淆矩阵

1.3.1 Accuracy

Accuracy，即准确率，表示预测正确的样本数量占总量的百分比，具体的公式如下：
$$Accuracy=\frac{TP+TN}{TP+FN+FP+TN}\text{\hspace{1em}(1-1)}$$

更通俗一点说，就是所有测试样本里预测对了几个。

讲到这里，我们不妨停下来思考一下，准确率的局限性。这是一件对于深度学习工作者非常重要的事情，这个指标能告诉我什么，不能告诉我什么，以这个指标来评价模型能否达到我的目的。如果这个指标不行的话，就得要用其他的指标。有一个好的指标，我们才能评价两个模型之间的好坏，才能去不断迭代优化模型。

我们所有的评估都是基于测试样本的，不难理解，测试样本的分布情况对评估的结果有着很大的影响。

举个例子，假设我们有黑白两色两种球，白球3个，黑球10个，模型的预测结果如下图1-6所示。

图1-14 模型预测结果示例

此时，$accuracy=\frac{1+10}{1+1+0+10}=0.92$，从评价指标上看，模型能力还行，但是这可能是一个大概率输出白，小概率输出黑的随机模型。也可能是一个对白球预测能力极强，对黑球预测能力极弱的模型。

从这个例子中，我们总结出三点：

• 测试样本需要尽可能类别平衡
• 测试样本数据量要大
• accuracy体现了模型在测试样本上的总体能力，没有更细粒度的类别指标

1.3.2 Precision和Recall

为了得到更细粒度的类别指标，就有了precision和recall。

Precision，即精确率，表示在预测为正例的结果中，有多少是正确的，具体公式如下：
$$Precision=\frac{TP}{TP+FP}\text{\hspace{1em}(1-2)}$$

Recall，即召回率，表示在实际的正例中，有多少被预测出来了，具体公式如下：
$$Recall=\frac{TP}{TP+FN}\text{\hspace{1em}(1-3)}$$

这里要注意的是，正例是我们人为定义的，定义白球为正例，则有
$$Precision=\frac{10}{11},Recall=\frac{10}{10}=1$$

定义黑球为正例，则有
$$Precision=\frac{1}{1}=1,Recall=\frac{1}{2}=0.5$$

每个类别都有自己的precision和recall，细粒度的评价指标就有了。

这里我们再停下来思考一下：
（1）Accuracy和这两个指标的有什么联系吗？
答：每个类别的Recall，就是每个类别的Accuracy，当测试样本中，只有正例时，Recall就等于Accuracy。比如我们在说目标检测的Recall的时候，是没有负例的，我们只有“前景”这样一个正例，此时的Recall就是Accuracy。从公式上看，只有正例时，$TN=FP=0$，Accuracy=Recall。换句话说，Accuracy是Recall的一种特殊情况。

对正例的定义，相当重要。

（2）Precision和Recall之间有什么联系？
分类时会设置一个置信度阈值，高于该阈值的被认为是正例，低于该阈值的被认为是负例，TP, FN, FP, TN随着置信度阈值的变化而变化。变化时，Precision和Recall是一个此消彼长的变化趋势，如下图1-7所示，该变化曲线包络的面积越大，证明模型的效果越好。面积比较难求，通常会看平衡点”（Break-Event Point，简称BEP）处的取值，这里不展开讲，感兴趣的可以看下参考资料3。

图1-15 Precision和Recall关系图

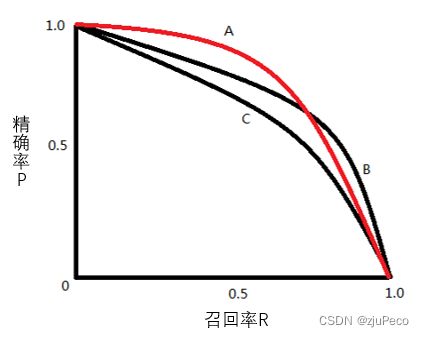
（3）置信度阈值确定时，每个类别两个指标，在一好一坏的情况下，很难评价两个模型的好坏，可以只用一个指标吗？
答：见下节的F1 Score。

1.3.3 F1 Score

F1 Score是Precision和Recall的调和平均，其定义为
$$F1=\frac{2}{\frac{1}{P}+\frac{1}{R}}=\frac{2\times P\times R}{P+R}\text{\hspace{1em}(1-4)}$$

下面举两个例子来看看F1 Score和Accuracy的区别

假设好苹果为正例

图1-16 示例1

$P=1$，$R=0.1$，所以有$F1=\frac{2\times 1\times 0.1}{1+0.1}=18.2\%$，$Accuracy=\frac{1+10}{1+9+0+10}=55\%$。

图1-17 示例2

$P=0.5$，$R=1$，所以有$F1=\frac{2\times 0.5\times 1}{0.5+1}=66.7\%$，$Accuracy=\frac{10+0}{10+0+10+9}=50\%$。

从这两个例子从可以看出，Accuracy更关注的正反例整体的预测情况，而F1-score更关注正例中的预测情况。

可以看出，这些指标都是根据需求不断改进的，没有哪个指标更正确，完全看场景和需求。指标的设计在现在仍旧不够完善，比如图像生成任务的评价指标仍是研究热点。

对于图像分类的任务，实际情况下，还是以Accuracy为主。

1.4 分类图像模型总体框架

对分类任务有了一个大概了解之后，来看下深度学习中处理分类问题的总体框架，如下图1-10所示。接下来的章节会对标明序号的部分做详细的说明。

图1-18 图像分类任务的总体框架图

2 线性分类器

2.1 图像的表示方法

图像的表示，也就是模型店输入。模型的输入可以有不同的形式，一个好的输入可以帮助模型屏蔽掉无用的信息，突出关键信息，是的模型更容易学习到关键特征。图像的表示方法可以总结为下图所示的几种，常用的还是像素值表示。

图2-1 图像表示方法

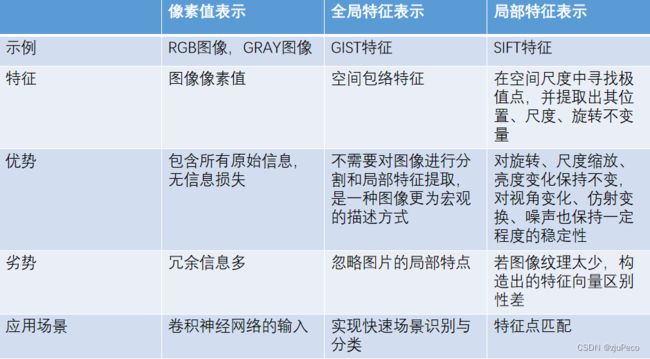
2.2 Cifar10数据集介绍

本文中使用到的数据集为Cifar10数据集，它出自于规模更大的一个数据集TinyImages，它有八千万张小图片，Cifar10是它的一个子集。

Cifar10包含 10 个类别的 RGB 彩色图 片：飞机（ airplane ）、汽车（ automobile ）、鸟类（ bird ）、猫（ cat ）、鹿（ deer ）、狗（ dog ）、蛙类（ frog ）、马（ horse ）、船（ ship ）和卡车（ truck ）。图片的尺寸为 32×32 ，数据集中一共有50000张训练图片和10000张测试图片。

图2-2 Cifar10数据集示例图

2.3 分类算法输入

大多数都分类算法都要求输入的是一个向量，本文将图片展开成一维的向量，这是一种最为简单粗暴的方式。

图2-3 图像转向量

一张RGB三通道的$32\times 32$的图片，展开称为向量后，其维度变为$1\times 3072$。

2.4 线性分类器

本文不涉及神经网络，只是讲深度学习的总体流程，所以分类模型选择了线性分类器。

线性分类器是一种线性映射，将输入的图像特征映射为类别分数，其特点是

• 形式简单、易于理解
• 通过层级结构（神经网络）或者高维映射（支撑向量机）可以 形成功能强大的非线性模型

假设共有$c$个类别，每个类别分别有一个线性分类器，第$i\in [1,2,...,c]$个分类器的定义为

$$f_i(x,w_i)=w_i^{T}x+b_i\text{\hspace{1em}(2-1)}$$

预测时，图片会分别输入每个分类器当中，取得分最高的类别为预测类别。

举一个实际的例子，假设一张超级简单的单通道图片，只有四个像素点，如下图2-4所示。

图2-4 输入示例

假设权重$w_i$和$b_i$已经全都学好，固定下来了，那么可以计算每个类别的得分，如下图2-5所示。

图2-5 类别得分示例

整个过程就是这么简单。

这里会有一个疑问，这个学出来的权重到底是个什么？由于权重$w_i$的维度和输入维度是一致的，我们将模型在$1\times 3072$输入上训练出来的权重还原回$32\times 32\times 3$的图像，可以得到下图2-6所示的结果。

图2-6 权重可视化

不难看出，对应类别的权重有着该类别的物体形状和颜色。我们不妨这样来想，不考虑$b_i$，线性分类器其实做了一个内积的操作，内积就是余弦距离，当两个向量之间的夹角越小，距离就越接近，内积就越大，分数也就越大。比如训练集只有一张图片，那么权重$w_i$等于这样图片就会是我们训练出来的结果。现在的结果可以理解为每个类别所有图片的均值。

权值可以看作是一种模板，输入图像与评估模板的匹配程度越高，分类器输出的分数就越高。

不过这个分类器也有很多的弊端：
（1）不同光照的影响
内积包括了两个向量的模长，如果将图像的每个像素点除以2，得分也会减半，但图像的类别没有变化。

（2）不同视角，不同尺度的影响
将图像旋转180度或是缩小一倍，模板就匹配不上了，得分也会骤减，但图像的类别没有变化。

（3）背景的影响
当物体很小时图片大部分区域都是背景，如果输入图片的背景和模板很相似，而类别换成了其他的物体，背景的得分占优，类别会被误判。

这些都是图像分类时需要解决的问题，很显然，简单的线性分类器，天然无法解决这些问题。关于分类器的设计，本文不讲，会在下一章中介绍。

线性分类器也可以认为学了一个决策面，如下图2-7所示。

图2-7 决策面示意图

3 损失函数

3.1 损失函数的定义

训练模型需要定义损失函数，训练的过程就是使得损失值不断减小的过程。

损失函数的通用定义可以表示为

$$L=\frac{1}{N}\sum _i{L}_i(f(x_i,W),y_i)\text{\hspace{1em}(3-1)}$$

其中，$x_i$表示数据集中的第$i$张图片；$f(x_i,W)$分类器对$x_i$的预测结果；$y_i$为样本$i$真实类别标签；$L_i$为第$i$个样本点的损失；$L$为数据集的总损失，它是数据集中所有样本损失的平均。

3.2 多类支持向量机损失

回到线性分类器的例子，这里用到的损失函数为

$$\begin{array}{rl}{L}_i& =\sum _{j\ne y_i}\{\begin{array}{ll}0,& if{s}_{i{y}_i}\ge s_{ij}+1\\ s_{ij}-s_{i{y}_i}+1& otherwise\end{array}\\ & =\sum _{j\ne y_i}\max (0,s_{ij}-s_{i{y}_i}+1)\end{array}\text{\hspace{1em}(3-2)}$$

其中，$j$表示类别标签，取值范围$[1,2,3,\dots ,c]$；$s_{ij}$表示第$i$个样本第$j$个类别的预测分数；$s_{i{y}_i}$表示第$i$个样本第$y_i$个类别的预测分数。

$$s_{ij}=f_i(x_i,w_j,b_j)=w_j^T{x}_i+b_j\text{\hspace{1em}(3-3)}$$

其中，$w_j$, $b_j$表示第$j$个类别分类器的参数；$x_i$表示数据集中的第$i$个样本。

这种$\max (0,\cdot )$形式的损失也被称为折页损失(hinge loss)。

图3-1 折页损失示意图

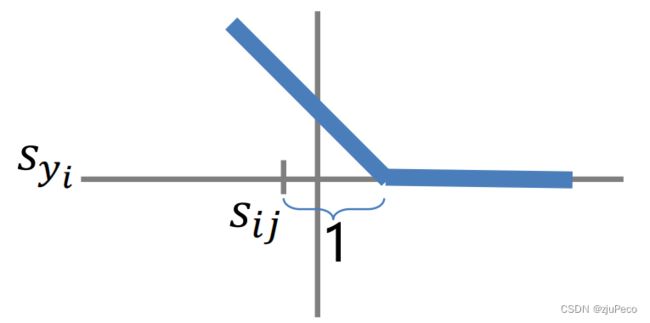
也就是当$s_{i{y}_i}\ge s_{ij}+1$后，我们就认为模型已经学习的够了，不需要进行步学习了。不过这里为什么是1，而不是$s_{i{y}_i}\ge s_{ij}+2$，而不是$s_{i{y}_i}\ge s_{ij}+10.6$。理论上这些取值都是可以的，但不同的值会对结果有一定的影响，取1是因为在这个任务中设计为了1，如果取不同值，影响不大，也就无所谓了。这些都是深度学习工作者需要思考的问题。

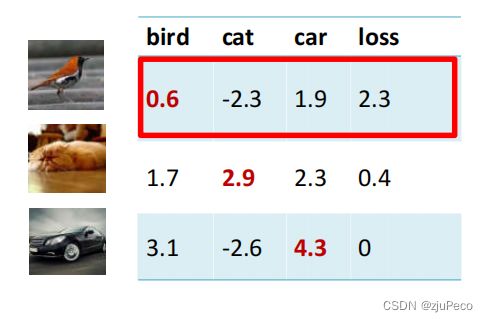
这里同样举一个例子。假设有3个类别的训练样本各一张，分类器对三个类别的打分如下所示：

图3-2 loss计算示例1

根据结果计算多类支持向量机损失，比如bird这一类的计算过程为

$$\begin{array}{rl}{L}_i& =\sum _{j\ne y_i}\max (0,s_{ij}-s_{i{y}_i}+1)\\ & =\max (0,-2.3-0.6+1)+\max (0,1.9-0.6+1)\\ & =2.3\end{array}\text{\hspace{1em}(3-4)}$$

所有结果如下图3-3所示。

图3-3 loss计算示例2

又到了思考的环节。对模型的改进，其实就是在不断质疑设计中的每一个细节的过程中产生的。

（1）$L_i$的最大值和最小值是多少？
答：最大值是无穷大，最小值为0。Loss的设计必须满足有最小值，不然模型会无止尽地训练下去。

（2）初始化时，$w$和$b$都为0，总损失$L$会是多少？
答：$w$和$b$都为0时，所有输出均为0，$L=c-1$。这其实可以用来检验代码有没有编写正确，如果$w$和$b$设置为0，输出不是$L=c-1$，那代码就有问题了。

（3）考虑所有类别（包括$j=y_i$），损失会有什么变化？
答：$L_i$会比原来大1，仅此而已。也就是${\sum }_{j\ne y_i}$可以改为${\sum }_j$，效果上不会有影响，只是计算更加方便。

（4）在计算总损失时，用求和代替平均会有什么影响？
答：总损失会放大N倍，效果上不会有影响。

（5）多标签的情况下，该损失是否适用？
答：不能直接适用，需要将Loss稍作修改，下式$(3-5)$是一种修改方式。预测的标签数量越多，损失越大。
$$L_i=\sum _{y_i\in Y}\sum _{j\notin Y}\max (0,s_{ij}-s_{i{y}_i}+1)\text{\hspace{1em}(3-5)}$$

（6）假设存在一个$W$使损失函数$L=0$，这个$W$是唯一的吗？
答：不唯一。

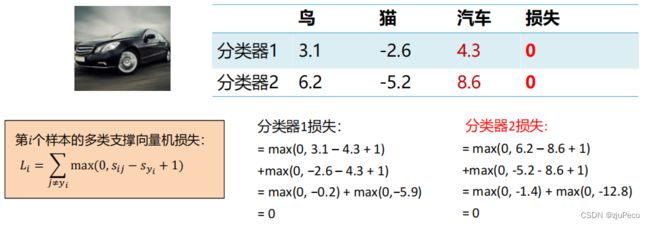
举个例子，假设两个线性分类器$f_1(x,W_1)=W_{1}x$，$f_2(x,W_2)=W_{2}x$，其中$W_2=2W_1$。对于下面图像，分类器1和分类器2的打分结果分别为

图3-4 分类器打分结果

可见两个不同的权重下，$L$都等于0。那么新的问题来了，如何在这两个权重中做选择呢？

这个时候，就该正则项出场了。

3.3 正则项

正则项的通用表示为$R(W)$，有了正则项的损失函数变为了

$$L(W)=\frac{1}{N}\sum _i{L}_i(f(x_i,W),y_i)+\lambda R(W)\text{\hspace{1em}(3-6)}$$

其中，$R(W)$为超参数，控制着正则损失在总损失当中的比重。

这里顺便说一下超参数的定义。超参数指的是在开始学习过程之前设置的参数，不是通过学习得到的。当然，现在也有许多学习超参数的方法，比如元学习，这里不展开讲。超参数对模型的性能有着重要的影响。

这里以式$(3-6)$中的$\lambda$为例，当$\lambda =0$时，优化结果仅与数据损失相关；当$\lambda =+\infty$时，优化结果与数据损失无关，仅考虑权重损失，此时系统最优解为$W=0$。

再举一个正则项的具体例子，L2正则项。
$$R(W)=\sum _k\sum _l{w}_{k,l}^2\text{\hspace{1em}(3-7)}$$

其中$k$表示类别序号，$l$表示$k$类别对应的第$l$个权重。

L2正则损失对大数值权值进行惩罚，喜欢分散权值，鼓励分类器将所有维度的特征都用起来，而不是强烈的依赖其中少数几维特征。

图3-5 L2损失示例

4 优化算法

4.1 优化算法目标

优化算法的作用时更新模型中的参数，也就是学习的过程。学习需要有目标，而损失函数就是我们的目标函数

$$L(W)=\frac{1}{N}\sum _i{L}_i(f(x_i,W),y_i)+\lambda R(W)\text{\hspace{1em}(4-1)}$$

我们的目标是求解使得$L(W)$最小的那组$W$。

直接求解，令$\frac{\partial L}{\partial W}=0$的做法通常不太现实，因为$L(W)$会是一个相当复杂的的复合函数。

通常通过梯度下降的方法，步步逼近最小值。

4.2 梯度下降算法

梯度下降涉及到两个问题，一个是往哪儿走？另一个是走多远？

图4-1 梯度下降示意图

先来看往哪儿走的问题。我们希望每走一步，损失函数的值可以减小一点，而且我们希望走同样的步长，沿着我们选择的方向走，损失值可以减小的更快，也就是通常说的下降得更快。

这个问题的答案是负梯度方向，我们来看下为什么。

借助于泰勒公式我们有

$$f(x+\delta )-f(x)\approx f’(x)\cdot \delta \text{\hspace{1em}(4-2)}$$

由于$f’(x)$和$\delta$都是向量，根据内积的定义有

$$f’(x)\cdot \delta =|f’(x)|\cdot |\delta |cos\theta \text{\hspace{1em}(4-3)}$$

目的是使得$f(x+\delta )$尽可能比$f(x)$小，故要使得$f’(x)\cdot \delta$负的最小，也就是$\theta =\pi$的时候。此时$f’(x)$和$\delta$方向相反，也就是负梯度方向。

至于另一个走多远的问题，答案就是由步长来决定。

在梯度下降时，是利用所有样本计算损失并更新梯度的。学习率可以控制步长。

图4-2 梯度更新示意图

4.3 梯度计算

计算梯度的方法主要分为两种，数值法和解析法。

（1）数值法
数值法对应于离散的求法，也就是参数发生小的变化，根据值发生对应的变化来计算梯度。其特点是计算量大，不精确。

举个例子，假设损失函数$L(w)=w^2$，求$w=1$点处的梯度。

$$\frac{dL(w)}{dw}=li{m}_{h\to 0}\frac{L(w+h)-L(w)}{h}\approx \frac{L(1+0.0001)-L(1)}{0.0001}=2.0001\text{\hspace{1em}(4-4)}$$

（2）解析法
解析法就是直接求导数的表达式，并代进去求解。其特点是精确，速度快，但导数函数推导易错。

还是以$L(w)=w^2$，求$w=1$点处的梯度为例。

$$\nabla L(w)=2w,{\nabla }_{w=1}L(w)=2\text{\hspace{1em}(4-5)}$$

实际求梯度时一般使用解析梯度，而数值梯度主要用于解析梯度的正确性校验（梯度检查）。

4.4 多类支持向量机损失函数梯度

回顾一下多类支持向量机损失函数为

$$L_i=\sum _{j\ne y_i}\max (0,(w_j^T{x}_i+b_j)-(w_{y_i}^T+b_{y_i})+1)\text{\hspace{1em}(4-6)}$$

对该式的$w_j$和$b_j$求偏导有
$$\begin{array}{rl}& \frac{\partial L_i}{\partial w_j}=\{\begin{array}{ll}0,& w_j^T{x}_i+b_j)-(w_{y_i}^T+b_{y_i})+1\le 0\\ x_i,& w_j^T{x}_i+b_j)-(w_{y_i}^T+b_{y_i})+1>0\end{array}\\ & \frac{\partial L_i}{\partial b_j}=\{\begin{array}{ll}0,& w_j^T{x}_i+b_j)-(w_{y_i}^T+b_{y_i})+1\le 0\\ 1,& w_j^T{x}_i+b_j)-(w_{y_i}^T+b_{y_i})+1>0\end{array}\end{array}\text{\hspace{1em}(4-7)}$$

4.5 随机梯度下降

在利用梯度下降的时候，每次都需要对所有样本求一次损失，复杂度是$O(n)$的。这样计算的开销太大。为了减小计算开销，我们可以放弃一点对方向的精度，于是就有了随机梯度下降法。

随机梯度下降的每次迭代中，我们随机平均采样一个样本索引$i\in 1,\dots ,n$，并计算梯度$\nabla f_i(x)$来迭代$x$：
$$x\leftarrow x-\eta \nabla f_i(x)\text{\hspace{1em}(4-8)}$$
$\eta$为学习率。可以看到每次迭代的计算开销从梯度下降的$O(n)$降到了常数$O(1)$。

讲到这里，也许会有疑问。这么算不对啊，梯度下降的复杂度是$O(n)$是因为它把所有的样本都看了一遍，如果随机梯度下降也把所有样本都看一遍的话，复杂度也是$O(n)$。这两者有什么区别吗？

有！大有区别！别忘了，梯度下降虽然方向准确，但是步长是不知道，为了不走过头，每次都只往正确的方向上走一小步，然后下次迭代时就又要重新计算了。随机梯度下降虽然方向不准确，但是每走一步都在修正方向，歪歪扭扭地，最终也能走到极小值点。同样是看一遍所有的数据，梯度下降只能走一步，随机梯度下降可以走$n$步。正是因为步长需要试探，使得随机梯度下降占了很大的优势。

5 数据处理

5.1 数据集的划分

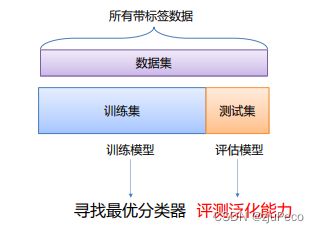
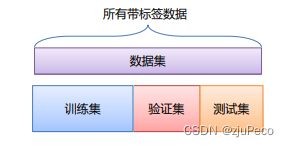
我们通常将数据集$D$划分为两个互斥的集合，其中一个集合作为训练集$S$，另一个作为测试集$T$，即$D=S\cup T$，$S\cap T=\varnothing$。在$S$上训练出模型后，用$T$来评估其效果。

图5-1 数据划分示意图-1

但是，这样会有一个问题。如果模型含有超参数（比如正则化强度），如何找到泛化能力更好的超参数？或者如何选择最佳的权重？直接的想法是，对比模型在不同超参数或权重下的测试集效果。这种做法可行吗？不可行！因为这样其实测试集已经被利用了，这用情况下，无法真实评估出模型的泛化能力。

解决方案是，适用验证集。

训练集用于给定的超参数时分类器参数的学习。验证集用于选择超参数和最佳权重。测试集评估泛化能力。

图5-2 数据划分示意图-2

问题又来了，如果数据很少，那么验证集包含的样本就太少，从而无法在统计上代表数据，怎么办？

一种方式叫做K折交叉验证。

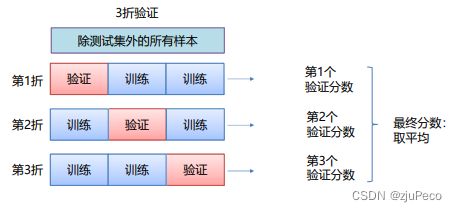
K折交叉验证将除测试集外的所有样本$D$划分为$k$个大小相似的互斥子集，即$D=D1\cup D2\cup \cdots \cup ，Di\cap Dj=\varnothing （i\ne j）$。每个子集都要尽可能保持数据分布的一致性，即从$D$中通过分层采样得到。然后用$(k-1)$个子集的并集作为训练集，余下的子集作为验证集。这样就可以获得$k$组训练/验证集，从而可以进行$k$次训练和验证，最终返回的是$k$个验证结果的均值，根据该值来选择合适的超参数和模型。交叉验证法评估结果的稳定性和保真性在很大程度上取决于$k$的取值。3折交叉验证如下图5-3所示。

图5-3 3折交叉验证示意图

选出的超参和模型最后可以通过以下两种方式得到最终模型：
（1）合并训练集和验证集，一并训练后，在测试集上测试其泛化能力。
（2）使用K折验证训练时分类器参数的均值，然后在测试集上测试器泛化能力。

为了避免随机性带来的影响，还有打乱数据的重复$k$折交叉验证。

图5-4 打乱数据的重复k折交叉验证示意图

带有打乱数据的重复$k$折交叉验证就是多次使用$k$折验证，在每次将数据划分为$k$个分区前，先将数据打乱。最终分数是多次$k$折验证分数的平均值。

5.2 数据的预处理

假设$x_1=1,2,3,\dots .$，$x_2=100,200,300,\dots$，对于模型$y={\sum }_i{w}_i{x}_i+b_i$，$L(w,b)=|y-\hat{y}|$显然，由于$x_1$的取值小，引起$y$的变化小，进而对$L$的影响也小，因此$w_1$方向的梯度就小。同理$w_2$方向的梯度就大。从而模型会更偏向$w_2$梯度的方向更新参数。

通过这个分析，我们发现要上$w_1$和$w_2$方向上的梯度相近，就应该使其相应的输入的取值在一个范围内。相应的方法就是特征归一化。

图像预处理中最常用的归一化是最大最小归一化（Min-Max Normalization），使结果值映射到$[0,1]$之间，转换函数如下：
$$x^{\prime }=\frac{x-min(x)}{max(x)-min(x)}\text{\hspace{1em}(5-1)}$$

最大最小归一化之所以适用于图像预处理，是因为最大最小值是固定的255和0，数值比较集中。

图5-5 归一化结果示意图

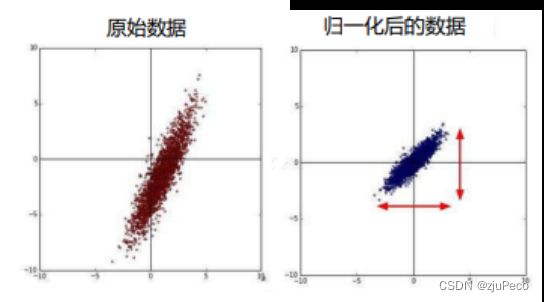
5.3 数据增广

数据增广是深度学习中常用的技巧之一，主要用于增加训练数据集，不仅可以让数据集尽可能的多样化，而且随机改变训练样本可以降低模型对于某些属性的依赖，从而提升模型的泛化能力。例如，可以对图像进行随机的平移，使感兴趣的物体出现在不同位置以减轻模型对出现位置的依赖项。也可以对图像进行随机裁剪，使得模型不依赖于对象的完整特征，从而通过局部特征也可以识别出物体。一个比较经典的数据增广库就是albumentations。

目前数据增广主要包括：

• 水平/垂直翻转
• 旋转
• 缩放
• 裁剪
• 平移
• 对比度
• 色彩抖动
• 噪声

图5-6 数据增广示意图

6 参考资料

[1] 计算机视觉与深度学习 北京邮电大学 鲁鹏 清晰版合集（完整版）
[2] 动手学深度学习-pytorch
[3] https://zhuanlan.zhihu.com/p/110015537