【矩阵论】2. 矩阵分解——单阵及特征值特征向量一些求法

矩阵论
1. 准备知识——复数域上的矩阵与换位公式)
1. 准备知识——复数域上的内积域正交阵
1. 准备知识——相似对角化与合同&正定阵
2. 矩阵分解—— SVD准备知识——奇异值
2. 矩阵分解——SVD
2. 矩阵分解——QR分解
2. 矩阵分解——乔利斯分解&平方根公式
2. 矩阵分解——正规谱分解——正规阵
2. 矩阵分解——正规分解
2. 矩阵分解——单阵及特征值特征向量一些求法

---

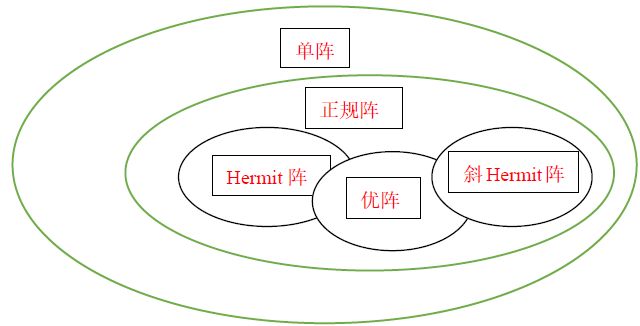
6.4 单阵

单阵A（又叫单纯阵，可对角阵），即满足 $P^{-1}AP=D=\left(\begin{array}{ccc}{\lambda }_1& & 0\\ & \ddots & \\ 0& & {\lambda }_n\end{array}\right)$ ，Q可逆，Q中列向量为A的特征向量

6.4.1 单阵谱公式

若A为单阵，全体不同特征根为 ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_k$ ，则有 $A={\lambda }_1{G}_1+\cdots +{\lambda }_k{G}_k$ 为A的谱分解

满足性质：
$$\begin{array}{rl}& ①G_1+G_2+\cdots +G_k=I\\ & ②G_1{G}_2=0,\cdots ,G_i{G}_j=0(i\ne j)\\ & ③G_1^2=G_1,\cdots ,G_k^2=G_k,但G_1^H=G_1,\cdots ,G_k^H=G_k不一定成立\\ & ④A^p={\lambda }_1^p{G}_1+\cdots +{\lambda }_k^p{G}_p,p=0,1,...\\ & ⑤f(A)=f({\lambda }_1)G_1+\cdots +f({\lambda }_k)G_k\\ & ⑥G_1=\frac{(A-{\lambda }_2)\cdots (A-{\lambda }_k)}{({\lambda }_1-{\lambda }_2)\cdots ({\lambda }_1-{\lambda }_k)},\cdots ,G_k=\frac{(A-{\lambda }_1)\cdots (A-{\lambda }_{k-1})}{({\lambda }_k-{\lambda }_1)\cdots ({\lambda }_k-{\lambda }_{k-1})}\\ & ⑦谱阵G_1,\cdots ,G_k中各列都是A的特征向量\end{array}$$
eg
$$A=\left(\begin{array}{cc}3& 1\\ 2& 2\end{array}\right),求A^{100}$$

$$\begin{array}{rl}& 由A是行和相等矩阵，所以行和4为特征值，\lambda (A)=\{4,tr(A)-4\}=\{4,1\}\\ & 故二阶阵有2个不同特征值，所以必为单阵\\ & G_1=\frac{A-{\lambda }_{2}I}{{\lambda }_1-{\lambda }_2}=\frac{1}{3}\left(\begin{array}{cc}2& 1\\ 2& 1\end{array}\right),G_2=-\frac{1}{3}\left(\begin{array}{cc}1& -1\\ -2& 2\end{array}\right)\\ & 可知A^{100}=4^{100}{G}_1+1^{100}{G}_2=\\ & 本例中，特向\left(\begin{array}{c}1\\ 1\end{array}\right),\left(\begin{array}{c}1\\ -2\end{array}\right)不正交，不是正规阵\end{array}$$

a. 单阵逆公式

$$\begin{array}{r}{A}^{-1}=\frac{1}{{\lambda }_1}{G}_1+\frac{1}{{\lambda }_2}{G}_2+\cdots +\frac{1}{{\lambda }_k}{G}_k\end{array}$$

其中A为单阵

b. 单阵函数公式

$$\begin{gathered} 若f_1(x),f_2(x),\cdots ,f_k(x)为x的k-1次多项式，则f_1(x)+f_2(x)+\cdots +f_k(x)=1 \\ 且f_1(A)+f_2(A)+\cdots +f_k(A)=I \end{gathered}$$

---

$$f_1(A),\cdots ,f_k(A)中非0列都是A的特征向量$$

6.4.2 单阵条件

a. 充分条件

若存在可逆阵P，使A相似于对角阵，则A为单阵
$$P^{-1}AP=D=\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_k\end{array}\right)$$

1. 正规阵为单阵

   

2. 设n阶方阵A恰有n个不同根 ${\lambda }_1,\cdots ,{\lambda }_n$ ,则A为单阵（必相似于对角阵）

   A为正规阵，则A必相似于对角阵

   证：A为正规阵，则存在U阵Q使 $Q^{H}AQ=\Lambda$ ，使A阵U相似于对角阵，故正规阵一定是单阵

3. A有n个无关的特征向量， $X_1,X_2,\cdots ,X_n$

   令 $P=\left(X_1,X_2,\cdots ,X_n\right)\Rightarrow P^{-1}AP=D$

4. 若每个k重根 $\lambda$ ，恰有k个特征向量，则A为单阵

   • 方程 $(A-{\lambda }_1)X=0$ 有 $n-r(A-{\lambda }_{1}I)$ 个基本解

     $\Rightarrow AX={\lambda }_{1}X有n-r(A-{\lambda }_{1}I)个基本解$

     $\Rightarrow r(A-{\lambda }_{1}I)=n-k$ ，${\lambda }_1$ 有k个特征向量 ，则A可能是单阵

     $\Rightarrow r(A-{\lambda }_{1}I)\ne n-k$ ，则A必不是单阵

   • eg1
     $$A=\left(\begin{array}{ccc}1& 1& 0\\ 0& 2& 0\\ 0& 0& 1\end{array}\right),\lambda (A)=\{2,1,1\}，{\lambda }_1=1为2重根$$
     验证A是否为单阵：
     $$\begin{array}{r}A-1I=\left(\begin{array}{ccc}0& 1& 0\\ 0& 1& 0\\ 0& 1& 0\end{array}\right),r(A-I)=1=3-2\therefore A是单阵\end{array}$$

   • eg2
     $$A=\left(\begin{array}{ccc}1& 1& 0\\ 0& 1& 0\\ 0& 0& 2\end{array}\right),\lambda (A)=\{2,1,1\}，{\lambda }_1=1为2重根$$
     验证A是否为单阵：
     $$A-1I=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right),r(A-I)=2\ne 3-2=1,\therefore A不是单阵$$

5. 设 ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_k$ 为A的全体不同根
   $$\begin{array}{rl}& 若(A-{\lambda }_{1}I)(A-{\lambda }_{2}I)\cdots (A-{\lambda }_{k}I)=0,则A为单阵(A相似与对角阵)\\ & 若(A-{\lambda }_{1}I)(A-{\lambda }_{2}I)\cdots (A-{\lambda }_{k}I)\ne 0,则A不是单阵\end{array}$$
   eg
   $$A=\left(\begin{array}{ccc}1& 1& 0\\ 0& 2& 0\\ 0& 1& 1\end{array}\right)是否为单阵，求A^{100}的谱公式$$

   $$\begin{array}{rl}& |A-\lambda I|=\left|\begin{array}{ccc}1-\lambda & 1& 0\\ 0& 2-\lambda & 0\\ 0& 1& 1-\lambda \end{array}\right|=(1-\lambda {)}^2(2-\lambda )=0,\therefore \lambda (A)=\{1,1,2\}\\ & 令{\lambda }_1=1,{\lambda }_2=2,(A-I)(A-2I)=\left(\begin{array}{ccc}0& 1& 0\\ 0& 1& 0\\ 0& 1& 0\end{array}\right)\left(\begin{array}{ccc}-1& 1& 0\\ 0& 0& 0\\ 0& 1& -1\end{array}\right)=0\\ & \therefore A为单阵\\ & 令G_1=\frac{A-{\lambda }_2}{{\lambda }_1-{\lambda }_2}=\left(\begin{array}{ccc}1& -1& 0\\ 0& 0& 0\\ 0& -1& 1\end{array}\right),G_2=I-G_1=\left(\begin{array}{ccc}0& 1& 0\\ 0& 1& 0\\ 0& 1& 0\end{array}\right)\\ & 得谱公式：A=1G_1+2G_2,且f(A)=f(1)G_1+f(2)G_2\\ & A^{100}=G_1+2^{100}{G}_2\end{array}$$

   ---

   上述判定方法也适用于分块阵
   $$\begin{array}{r}A=\left(\begin{array}{ccc}2& 1& 0\\ 1& 2& 0\\ 0& 0& 2\end{array}\right)=\left(\begin{array}{cc}{A}_1& 0\\ 0& A_2\end{array}\right),求A^{100}\end{array}$$

   $$\begin{array}{rl}& 由A_1阵为行和阵，特征值\lambda (A_1)=\{3,tr(A_1)-3\}=\{3,1\}\\ & (A_1-3I)(A_1-2I)=\left(\begin{array}{cc}-1& 1\\ 1& -1\end{array}\right)\left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right)=0,\therefore A_1为单阵\\ & 故有谱分解A_1=3G_1+G_2=3\frac{A_1-{\lambda }_2}{{\lambda }_1-{\lambda }_{2}I}+\frac{A-{\lambda }_{2}I}{{\lambda }_2-{\lambda }_1}=3\ast \frac{1}{2}\left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right)+\frac{1}{2}\left(\begin{array}{cc}1& -1\\ -1& 1\end{array}\right)\\ & A_1^{100}=3^{100}{G}_1+1G_2=\frac{3^{100}}{2}\left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right)+\frac{1}{2}\left(\begin{array}{cc}1& -1\\ -1& 1\end{array}\right)\\ & A_2^{100}=(2^{100})\\ & \therefore A^{100}=\left(\begin{array}{cc}{A}_1^{100}& \\ & A_2^{100}\end{array}\right)=\left(\begin{array}{ccc}\frac{3^{100}+1}{2}& \frac{3^{100}-1}{2}& 0\\ \frac{3^{100}-1}{2}& \frac{3^{100}+1}{2}& 0\\ 0& 0& 2^{100}\end{array}\right)\end{array}$$

b. 单阵充要条件：0化式判别法

$$A为单阵⟺极小式m(x)无重根；若m(x)有重根，则A不是单阵$$

单阵判定与极小式

$$\begin{gathered} 若{\lambda }_1,\cdots ,{\lambda }_k为不同根，且(A-{\lambda }_{1}I)(A-{\lambda }_{2}I)\cdots (A-{\lambda }_{k}I)=0,则A必为单阵 \\ 此时称m(x)=(x-{\lambda }_1)(x-{\lambda }_2)\cdots (x-{\lambda }_k)为A的极小式 \end{gathered}$$

0化式与极小式定义

$$\begin{array}{rl}& 若多项式f(x)使f(A)=0,则称f(x)为A的0化式\\ & 若m(A)=0且m(x)有最小次数，则m(x)为A的极小式，即极小式为次数最少的0化式\end{array}$$

• eg1：
  $$\begin{array}{rl}& A=I=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),满足A^2=I，可知f(x)=x^2-1=0,且f(A)=A^2-I=0\\ & f(x)=x^2-1=(x-1)(x+1)为A的0化式\\ & \because A-I=0,\therefore x-1也是A的0化式，且m(x)=x-1为极小式\end{array}$$

• eg2:
  $$\begin{array}{rl}& A=\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)，A^2=I,即A^2-I=0,\\ & f(x)=x^2-1=(x-1)(x+1)为A的0化式，但由于A-I\ne 0且A+I\ne 0\\ & 故A的极小式m(x)=x^2-1\end{array}$$

若f(x)=0无重根，且f(A)=0,则A必为单阵

定理：

• 若f(A)=0，则f(A)g(A)=0,可知f(x)g(x)也是0化式

• 特征多项式 $f(x)=|xI-A|=a_0+a_{1}x+a_2{x}^2+\cdots +a_n{x}^n$ 一定是0化式

  即 $f(A)=a_0+a_{1}A+\cdots +a_n{A}^n=0$

• 极小式为特征多项式的因式，可表示为 $|xI-A|=m(x)g(x)$

• 极小式必为每个0化式f(x)的因子，即若f(A)=0，则f(x)=m(x)g(x)

极小式求法

1. 对于 $|xI-A|=(x-a{)}^2(x-b)$

   • 若 $(A-aI)(A-bI)=0$ ，则极小式为 $m(x)=(x-a)(x-b)$

   • 若 $(A-aI)(A-bI)\ne 0$ ，则极小式为 $m(x)=(x-a{)}^2(x-b{)}^2$

2. 对于 $|xI-A|=(x-a)(x-b)(x-c)$ ，则极小式为 $m(x)=(x-a)(x-b)(x-c)$

应用

1. 列出特征方程，求出极小式，即证明A是单阵
2. 根据极小式，写出单阵谱分解
3. 计算f(A)

$$A=\left(\begin{array}{ccc}2& 2& 1\\ 1& 3& 1\\ 1& 2& 2\end{array}\right)，求A的谱分解p$$

$$\begin{array}{rl}& \begin{array}{c}|A-\lambda I|=(x-5)(x-1{)}^2,且(A-5I)(A-I)=0\Rightarrow A为单阵\end{array}\\ & \Rightarrow 单阵A有谱分解A=5G_1+G_2=\end{array}$$

---

$$\begin{gathered} A=\left(\begin{array}{ccc}1& 1& 0\\ 0& 2& 0\\ 0& 0& 3\end{array}\right),求谱分解 \\ A为上三角阵，所以A有三个互异特征根1,2,3，极小式为(x-1)(x-2)(x-2)=0 \\ 故A由谱分解A=G_1+2G_2+3G_3 \end{gathered}$$

7.1 特根

$$若n阶方阵A=(a_{ij})中"行和=常数k"，则常数k为A的一个特征根，全1向量X=\left(\begin{array}{c}1\\ ⋮\\ 1\end{array}\right)为A的一个特向$$

$$若n阶方阵A=(a_{ij})中“列和=常数k”,则常数k为A^T的一个特根，全1向量=\left(\begin{array}{c}1\\ ⋮\\ 1\end{array}\right)为A的一个特向$$

可知 $A^H$ 与 A 的特征值相等，但特征向量未必相等

eg

---

$$\begin{array}{rl}& 已知二阶阵A=\left(\begin{array}{cc}3& 1\\ 2& 2\end{array}\right)(行和阵),特根为4,tr(A)-4=1,相应特向X=\left(\begin{array}{c}1\\ 1\end{array}\right),Y=\left(\begin{array}{c}1\\ -2\end{array}\right)\\ & X，Y线性无关，所以P=\left(X,Y\right)=\left(\begin{array}{cc}1& 1\\ 1& -2\end{array}\right)为可逆阵，故A可相似对角化为对角阵\\ & P^{-1}AP=D=\left(\begin{array}{cc}4& 0\\ 0& 1\end{array}\right),故可知A为单阵\end{array}$$

7.1.1 实对称阵特根为实数

7.2 特征向量

$$若(A-{\lambda }_{1}I)P=0,则P中的列都是{\lambda }_1的特征向量$$

证明：
$$\begin{array}{rl}& (A-{\lambda }_{1}I)P=0⟺AP={\lambda }_{1}P,令P=(X_1,\cdots ,X_n)，按列分块，则有\\ & A(X_1,\cdots ,X_n)={\lambda }_1(X_1,\cdots ,X_n)\Rightarrow (A{X}_1,\cdots ,A{X}_n)=({\lambda }_1{X}_1,\cdots ,{\lambda }_n{X}_n)\\ & 则P中各列都是{\lambda }_1的特征向量\end{array}$$

7.2.1 两个互异特根的特向

$$若(A-{\lambda }_{1}I)(A-{\lambda }_{2}I)=0,则(A-{\lambda }_{2}I)的列都是{\lambda }_1的特向，(A-{\lambda }_{1}I)的列是{\lambda }_2的特向$$

eg：
$$\begin{array}{rl}& A=\left(\begin{array}{ccc}1& 0& -2\\ 0& 0& 0\\ -2& 0& 4\end{array}\right)(为正规H单阵)，全体特征根\lambda (A)=\{5,0,0\},不同特征根为5,0\\ & 由于A是单阵，必有(A-{\lambda }_{1}I)(A-{\lambda }_{2}I)=(A-5I)(A-0I)=0\\ & 其中，{\lambda }_1=5对应的特征向量为A中的一个列向量\left(\begin{array}{c}1\\ 0\\ -2\end{array}\right)，\\ & {\lambda }_2=0对应的特征向量为A-5I=\left(\begin{array}{ccc}-4& 0& -2\\ 0& -5& 0\\ -2& 0& -1\end{array}\right)的列向量\\ & 分别为\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)\left(\begin{array}{c}2\\ 0\\ 1\end{array}\right)\end{array}$$

---

7.2.2 幂等阵的一个特向

$$若A为幂等阵：A^2=A，则必有(A-I)A=0,则A中的列都是{\lambda }_1=1的特征向量$$

如：
$$A=\left(\begin{array}{cc}1& 0\\ -1& 0\end{array}\right),A^2=A为幂等阵，则A中非0列\left(\begin{array}{c}1\\ -1\end{array}\right)是{\lambda }_1=1的特征向量$$

7.2.3 三个互异特根的特向

$$\begin{array}{rl}若& (A-{\lambda }_{1}I)(A-{\lambda }_{2}I)(A-{\lambda }_{3}I)=0,则\\ & (A-{\lambda }_{2}I)(A-{\lambda }_{3}I)中非零列为{\lambda }_1的特向\\ & (A-{\lambda }_{1}I)(A-{\lambda }_{3}I)中非零列为{\lambda }_2的特向\\ & (A-{\lambda }_{1}I)(A-{\lambda }_{2}I)中非零列为{\lambda }_3的特向\end{array}$$

eg

$$A=\left(\begin{array}{ccc}-1& i& 0\\ -i& 0& -i\\ 0& i& -i\end{array}\right)，求特征向量$$

$$\begin{array}{rl}& 由特征多项式计算得\lambda (A)=\{1,-1,2\}，3阶方阵有3个互异特征根，故A为单阵\\ & 且有0化式(x-1)(x+1)(x-2)成立，即(A-I)(A+I)(A-2I)=0成立，\\ & 可知{\lambda }_1=1,{\lambda }_2=-1,{\lambda }_3=2对应的特征向量\\ & 分别为(A+I)(A-2I),(A-I)(A-2I),(A-I)(A+I)的列向量,即有X_1=\left(\begin{array}{c}1\\ -2i\\ 1\end{array}\right)\\ & X_2=\left(\begin{array}{c}-1\\ 0\\ 1\end{array}\right),X_3=\left(\begin{array}{c}1\\ i\\ 1\end{array}\right),可令U阵Q=\left(\frac{X_1}{\sqrt{6}},\frac{X_2}{\sqrt{2}},\frac{X_3}{\sqrt{3}}\right),必有Q^{-1}AQ=D=\left(\begin{array}{ccc}1& & \\ & -1& \\ & & -2\end{array}\right)\end{array}$$

7.2.4 重根的特向

$$\begin{array}{rl}& 若(A-{\lambda }_I{)}^2=0,则(A-\lambda I)中非0列都是\lambda 的特向\\ & SP:若A^2=0,则A中非0列都是\lambda 的特向\end{array}$$

eg

---

$$A=\left(\begin{array}{ccc}2& 0& 0\\ 1& 1& 1\\ 1& -1& 3\end{array}\right)，其A的特向$$

$$\begin{array}{rl}& \lambda (A)=\{2,2,2\},0化式为(x-2{)}^3，且(A-2I{)}^2=\left(\begin{array}{ccc}0& 0& 0\\ 1& -1& 1\\ 1& -1& 1\end{array}\right)\left(\begin{array}{ccc}0& 0& 0\\ 1& -1& 1\\ 1& -1& 1\end{array}\right)=0\\ & 可见其特向为\left(\begin{array}{c}0\\ 1\\ 1\end{array}\right),且三重根\lambda =2只有一个特向，所以A不是单阵\end{array}$$

7.3 交换定理与公共特征向量

$$\begin{gathered} 若方阵AB=BA(可交换)，任取A的特根的特向X，满足AX=\lambda X,BX=tX \\ 即X是A和B的公共特征向量 \end{gathered}$$

$$若A，B为n阶实对称阵，且可交换AB=BA，则存在正交阵Q，使Q^{-1}AQ,Q^{-1}BQ为对角阵$$