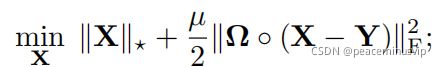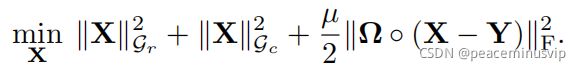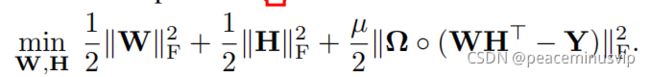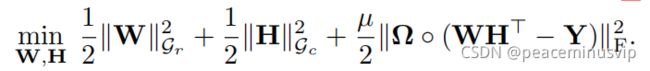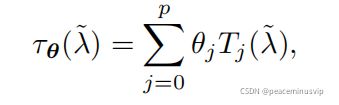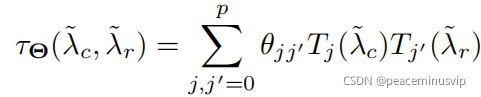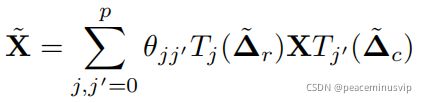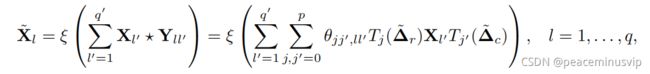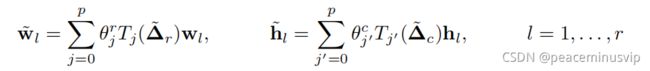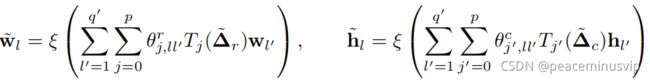图表示学习——MGGCN 19年记录

论文题目

Geometric Matrix Completion with Recurrent Multi-Graph Neural Networks——NIPS2017

 论文链接：

https://proceedings.neurips.cc/paper/2017/file/2eace51d8f796d04991c831a07059758-Paper.pdfhttps://proceedings.neurips.cc/paper/2017/file/2eace51d8f796d04991c831a07059758-Paper.pdf

 文章背景

最近的工作表明，当引入user/item之间以graph形式的成对关系并且在这些图上施加光滑先验，这些技术的性能得到了提高，然而，这种技术并不完全利用user/item图形上的局部固定结构，而且要学习的参数是线性的。我们提出了一种利用图形的几何深度学习来克服这些局限性的新方法。

创新点：

矩阵完成结构结合了一种新的多图卷积神经网络（Multi-graph convolutional neural network)，(MGCNN)它可以从用户和项中学习有意义的统计图结构模式，以及在分数矩阵上应用可学习扩散的递归神经网络(RNN)。介绍了一种新的multi-graph CNN架构，这种新结构能够同时从多个图上定义的信号中提取局部平稳模式。  （局部：希望只影响到一个像素附近的像素）

multi-graph CNN被用来由user和item图编码的行和列相似性从得分矩阵中提取局部稳定特征。 然后，将这些空间特征馈送到RNN中，该RNN逐渐扩散得分值，重建矩阵。

相关知识

1. Matrix completion（矩阵补全）：

给定矩阵中已知元素的一小部分，目标是填充其余元素。推荐方法可以作为矩阵补全问题提出。 （1）列：用户（user）       行：项（item）       矩阵值： 用户是否想要这个item的得分。

（2）把几何结构融入矩阵补全问题——以表示用户（user）和项目（item）的相似性的列图和行图的形式

1.1矩阵补全问题

X是要补充的矩阵； 核范数——奇异值之和

Ω是已知条目Ω的指示矩阵。

Y是已知矩阵

◦表示Hadamard点态积（二者对应位置的乘积） 

1.2 Geometric matrix completion（几何矩阵补全）

1.2.1最简单的结构是邻近结构——加权无向图

（1）列图：

  

列图可以被认为是一个社会网络，捕捉用户之间的关系和他们的爱好的相似性。

（2）行图：     代表item之间的相似性

 1.2.2 根据行图或者列图构造正规化的图拉普拉斯矩阵

 

D代表着度数矩阵（是一个对角矩阵，无向图n*n）   W是邻接矩阵(n*n)

∆r:表示与行图相关联的拉普拉斯图。  

∆c:表示列图相关联的拉普拉斯图 若将矩阵X的列当作列图Gc 的向量值函数；

X的行当作行图Gr的向量值函数 则切比雪夫范数：

 因此，几何矩阵完成问题归结为最小化：

 

 1.2.3.分解模型

存在问题：公式中的变量是全m×n矩阵X，因此很难扩展到大矩阵。

解决方案：分解X = WHT   （W:m*r    H:n*r）

核范数最小化问题可以用分解形式重写为

 

所以基于图的极小化问题的分解公式：

2.Deep learning on graphs（图上的深度学习——GCN）

 

几何深度学习——CNN在图上的推广

关于图顶点的函数        ；

表示正交特征向量的矩阵

图傅里叶变换

两个函数x，y的卷积可定义为各自傅里叶变换的元素乘积，

 

（y当作过滤函数——拉普拉斯矩阵函数 diag(ˆy1, . . . , yˆn) ——当作矩阵L的特征值函数）

滤波器系数表示为        τ(λ)是频率λ的平滑传递函数。

经过一系列转化，利用Chebyshev多项式递归计算卷积核 

 

解决方案

1.multi-graph CNN  （与GCN很像）

1.1 

经典的二维傅里叶变换的图像(矩阵)可以认为是应用一维傅里叶变换的行和列。 

二维傅里叶变换的形式： 

Φc：∆c（拉普拉斯列图n*n）的特征向量               Φr：∆r（拉普拉斯行图m*m）的特征向量

(1)若使用谱卷积（当作二维图像光谱域的过滤）： 

(2)假设多图滤波器在频谱域中表示为两个频率的光滑函数：

使用p阶切比雪夫来表示滤波器

 

(3)多图形滤波器在矩阵X中的应用：

 

· 按比例缩放的拉普拉斯算子

（4）采用滤波器参数化的多图卷积层应用于q‘输入信道：也就是q'个输入X（m*n大小）q个输出 、

 

可以将几层堆叠在一起,就是multi-graph CNNs

1.2 分离卷积（之前的X是一个完整的矩阵）

根据X=WHT的因式分解，可以简化多图卷积（将一维卷积应用到每个分解的因子）

Wl，hl表示因子W，H的第l列。

and 行和列的切比雪夫系数向量

相应的，卷积层就是：    这个就是sMGCNN

 

2. RNN递归神经网络（综合起来可以看作是一个可学习的扩散过程，它重建了分数矩阵） 

 下一步是将MGCNN或sMGCNN从矩阵提取的空间特征馈送到递归神经网络（RNN），实现扩散过程，逐步重建得分矩阵,

若不使用RNN：为了组合稀疏输入矩阵中可用的少数分数，多层CNN将需要非常大的滤波器或许多层来跨矩阵域扩散分数信息。

使用RNN：而基于扩散的方法允许仅通过施加适当数量的扩散迭代来重建缺失的信息。这样就有可能处理极其稀少的数据，同时又不需要过多的模型参数。

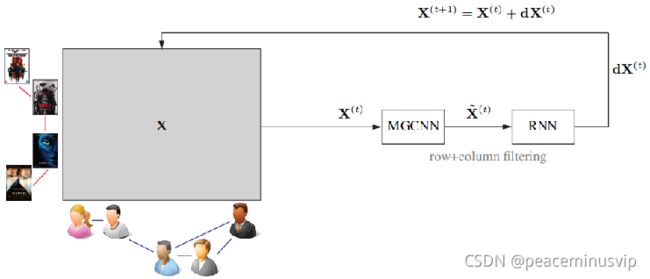
2.1 Recurrent MGCNN (RMGCNN)（在full-matrix上补充）

 

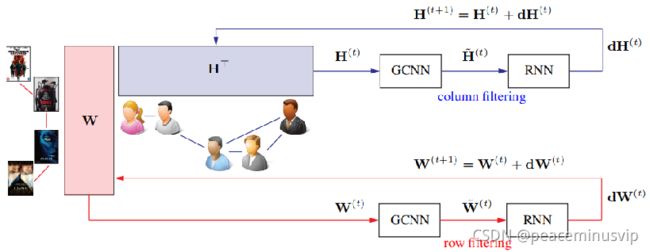
2.2  separable RMGCNN (sRMGCNN 在分解因式的矩阵上X=WHT) 

 

 

 算法

 3.训练——基于图的最小化问题（几何矩阵补充）

全矩阵补充训练

分解的矩阵

 

总结和思考

1）多图卷积怎么做

2）为什么RMGCNN和sRMGCNN一个是行列一起卷，一个是行和列分开卷          

RMGCNN：使用全矩阵完成模型并同时在矩阵X的行和列上同时操作的递归MGCNN(RMGCNN)体系结构。学习复杂性是O(MN)。        

sRMGCNN：可分离递归MGCNN(SRMGCNN)结构采用分解矩阵完成模型，分别对因子W，HT的行和列进行操作。学习复杂度为O(Mn)。

3）GCNN+RNN有什么好处？

将MGCNN或sMGCNN从矩阵提取的空间特征馈送到递归神经网络（RNN），实现扩散过程，逐步重建得分矩阵,

若不使用RNN：为了组合稀疏输入矩阵中可用的少数分数，多层CNN将需要非常大的滤波器或许多层来跨矩阵域扩散分数信息。

使用RNN：而基于扩散的方法允许仅通过施加适当数量的扩散迭代来重建缺失的信息。这样就有可能处理极其稀少的数据，同时又不需要过多的模型参数。

4）邻居图如何构造？

对于MovieLens数据集，分别在用户特征空间和电影特征空间中将用户图和项(电影)图构造为未加权的10最近邻图。

对于Flixster，用户图和项图是根据原始矩阵的分数构造的。

对于Douban数据集，只使用了用户图（以社交网络的形式提供）

对于YahooMusic数据集，只使用项目图，在项目特征空间(艺术家、专辑和类型)中使用未加权的10近邻构造的项图。