插补搜寻法之算法分析及实现

插补搜寻简介

插补方式有:直线插补,圆弧插补,抛物线插补,样条线插补等，我们这里用到的是直线插补。

直线插补（Llne Interpolation）这是车床上常用的一种插补方式，在此方式中，两点间的插补沿着直线的点群来逼近，沿此直线控制刀具的运动。

对于一个有序数组，一般我们可以使用二分查找发查找某一个元素，这里介绍另一种方法，插补（Interpolation）搜寻法。和二分查找直接用中间的元素和要找的元素比较不一样，该算法利用数据分布近似直线来做比例运算，求得一个索引和要找的元素比较。

如果却搜寻的资料分布平均的话，可以使用插补搜寻法来进行搜寻，在搜寻的对象比较多时，插补搜寻法会比二分搜寻法来的快速。有的书上说插补查找算法比二分查找速度快，我在同一台机器上使用百万级数据测试发现，事实上并不是这样。插补查找可能收敛的速度的确比二分快一些，但是它的运算过程中用到了乘法和除法这些耗时的运算，所以实际效果并没有二分查找的速度快。

插补搜寻算法分析

插补搜寻法是以资料分布的近似直线来作比例运算，以求出中间的索引并进行资料比对，如果取出的值小于要寻找的值，则提高下界，如果取出的值大于要寻找的值，则降低下界，如此不断的减少搜寻的范围，所以其本原则与二分搜寻法是相同的，至于中间值的寻找是透过比例运算，如下所示，其中K是指定要寻找的对象， 而m则是可能的索引值：

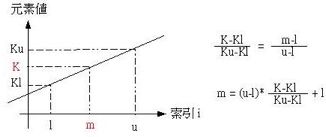
假设数组为a,下届为low,上届为high,要找的元素的K，则求得中间值为m
在二分查找中,m = low + (high - low) /2;
在插补查找中,m = low + (high - low) * (K - a[low]) / (a[high] - a[low])。

插补搜寻算法实现（C/OC）

 

#define MAX 100

#define SWAP(x,y) {int t; t = x; x = y; y = t;}

 

//主程序（C/OC）

int number[MAX] = {0};

int i, find;

srand(time(NULL));                      //产生随机数种子

for(i = 0; i < MAX; i++) {              //产生随机数组

    number[i] = rand() % 100;

}

quicksort(number, 0, MAX-1);            //快速排序，是数组变成有序的



printf("数列：");

for(i = 0; i < MAX; i++)

    printf("%d ", number[i]);

find = 11;                              //被搜索的数字

if((i = intsrch(number, find)) >= 0)    //调用插入排序法

    printf("\n找到数字于索引 %d ", i);

else

    printf("\n找不到指定数");

printf("\n"); 

 

//插补搜寻法

int intsrch(int number[], int find) {   

    int low, mid, upper;

    

    low = 0;

    upper = MAX - 1;

    

    while(low <= upper) {

        mid = (upper-low)*

        (find-number[low])/(number[upper]-number[low])

        + low;                          //核心算法的实现

        if(mid < low || mid > upper)    //为找到，查询结束

            return -1;

        

        if(find < number[mid])

            upper = mid - 1;

        else if(find > number[mid])

            low = mid + 1;

        else                            //查询成功

            return mid;

    }

    

    return -1;

}



//快速排序法

void quicksort(int number[], int left, int right) { 

    int i, j, k, s;

    

    if(left < right) {

        s = number[(left+right)/2];                 //以中间值为基准

        i = left - 1;

        j = right + 1;

        

        while(1) {

            while(number[++i] < s) ;                // 向右找

            while(number[--j] > s) ;                // 向左找

            if(i >= j)

                break;

            SWAP(number[i], number[j]);

        }

        

        quicksort(number, left, i-1);               // 对左边进行递回

        quicksort(number, j+1, right);              // 对右边进行递回

    } 

}