- cs231n_深度之眼第二次作业
Jie_Cheney
图像分类数据和label分别是什么?图像分类存在的问题与挑战?图像分类数据包括训练集测试集的数据,在有监督的问题中对于训练集数据来说是有label的,而测试集是等待我们去识别它的类别,不具有label。label就是分类标签,比如cifar10这个数据集,待分类的这10类数据我们可以写成1-10,或者0-9这就叫做label。图像分类存在的问题与挑战:光照,角度,形变,遮挡。使用python加载一
- 向量,矩阵和张量的导数 | 简单的数学
橘子学AI
前段时间看过一些矩阵求导的教程,在看过的资料中,尤其喜欢斯坦福大学CS231n卷积神经网络课程中提到的Erik这篇文章。循着他的思路,可以逐步将复杂的求导过程简化、再简化,直到发现其中有规律的部分。话不多说,一起来看看吧。作者:ErikLearned-Miller翻译:橘子来源:橘子AI笔记(datawitch)本文旨在帮助您学习向量、矩阵和高阶张量(三维或三维以上的数组)的求导方法,以及如何求对
- cs231n assignment1——SVM
柠檬山楂荷叶茶
cs231n支持向量机python机器学习
整体思路加载CIFAR-10数据集并展示部分数据数据图像归一化,减去均值(也可以再除以方差)svm_loss_naive和svm_loss_vectorized计算hinge损失,用拉格朗日法列hinge损失函数利用随机梯度下降法优化SVM在训练集和验证集计算准确率,保存最好的模型在测试集进行预测计算准确率加载展示划分数据集加载CIFAR-10数据集#LoadtherawCIFAR-10data.
- (2023版)斯坦福CS231n学习笔记:DL与CV教程 (12) | 视觉模型可视化与可解释性(Visualizing and Understanding)
女王の专属领地
计算机视觉#计算机视觉#学习笔记
前言笔记专栏:斯坦福CS231N:面向视觉识别的卷积神经网络(23)课程链接:https://www.bilibili.com/video/BV1xV411R7i5CS231n:深度学习计算机视觉(2017)中文笔记:https://zhuxiaoxia.blog.csdn.net/article/details/801551662023最新课程PPT:https://download.csdn.
- 2019-02-25~~2019-03-03 第十周周末复盘
仰望星空的小狗
一、任务清单1、刷leetcode题目(7道)2、听tensorflow,cs231n和cv课程3、技术文档输出4、恢复早起的作息二、反思1、自从年前工作非常忙,加上遇上一些郁闷的事情,导致年前到现在时间记录中断了很长一段时间。本周开始恢复时间记录,日打卡,周复盘。2、生活中不论谁,肯定会时不时遇上一些令人郁闷的事情,这些郁闷的事情很可能会打乱原本的生活节奏。但是,生活还有很长的路要走,不应该因为
- 训练神经网络(上)激活函数
笔写落去
深度学习神经网络人工智能深度学习
本文介绍几种激活函数,只作为个人笔记.观看视频为cs231n文章目录前言一、Sigmoid函数二、tanh函数三、ReLU函数四、LeakyReLU函数五、ELU函数六.在实际应用中寻找激活函数的做法总结前言激活函数是用来加入非线性因素的,提高神经网络对模型的表达能力,解决线性模型所不能解决的问题。一、Sigmoid函数这个函数大家应该熟悉在逻辑回归中曾用到这个sigmoid函数这个函数可以将负无
- 卷积神经网络
weixin_34283445
人工智能
https://zhuanlan.zhihu.com/p/27642620关于卷积神经网络的讲解,网上有很多精彩文章,且恐怕难以找到比斯坦福的CS231n还要全面的教程。所以这里对卷积神经网络的讲解主要是以不同的思考侧重展开,通过对卷积神经网络的分析,进一步理解神经网络变体中“因素共享”这一概念。注意:该文会跟其他的现有文章有很大的不同。读该文需要有本书前些章节作为预备知识,不然会有理解障碍。没看
- CS231n 作业答案
tech0ne
CS231n三次大作业:#第一次作业##原始包下载:作业一完成包地址:作业一JupyterNotebook结果:KNNSVMSoftmaxTwolayernetFeatures第二次作业原始包下载:作业二完成包地址:作业二JupyterNotebook结果:FullyConnectedNetsBatchNormalizationDropoutConvolutionalNetworksTensorf
- cs231n作业-assignment1
momentum_
AIpython机器学习numpy
assignment1(cs231n)文章目录assignment1(cs231n)KNN基础计算distances方法一:双层循环计算distances方法二:单层循环计算distances方法三:无循环根据dists找到每个测试样本的种类KNN模型汇总交叉验证KNN基础计算distances方法一:双层循环dists矩阵是(num_test,num_train)500*5000defcompu
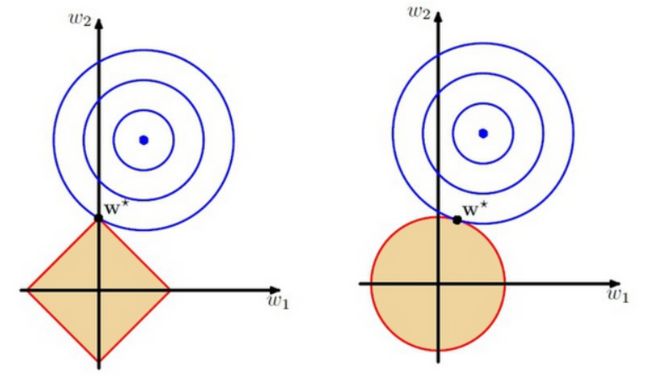
- 【深度学习理论】(1) 损失函数
立Sir
深度学习理论机器学习人工智能神经网络深度学习损失函数
各位同学好,最近学习了CS231N斯坦福计算机视觉公开课,讲的太精彩了,和大家分享一下。已知一张图像属于各个类别的分数,我们希望图像属于正确分类的分数是最大的,那如何定量的去衡量呢,那就是损失函数的作用了。通过比较分数与真实标签的差距,构造损失函数,就可以定量的衡量模型的分类效果,进而进行后续的模型优化和评估。构造损失函数之后,我们的目标就是将损失函数的值最小化,使用梯度下降的方法求得损失函数对于
- 线性分类器--数据处理
骆驼穿针眼
计算机视觉与深度学习深度学习
数据集划分通常按照70%,20%,10%来分数据集数据处理斯坦福的线性分类器体验http://vision.stanford.edu/teaching/cs231n-demos/linear-classify/
- 【CS231n】-学习笔记-1-Intro to Computer Vision, historical context.
Alice熹爱学习
计算机视觉计算机视觉CS231nDeepLearningPYTHON
Class:http://cs231n.stanford.eduSchedule:http://cs231n.stanford.edu/syllabus.htmlSlides:http://vision.stanford.edu/teaching/cs231n/slides/winter1516_lecture1.pdfVideo:https://www.youtube.com/watch?v=N
- 笔记00-杜克大学公开课,图像和视频处理:从火星到好莱坞
木木爱吃糖醋鱼
笔记内容介绍》ImageandVideoProcessing:FromMarstoHollywoodwithaStopattheHospital算起来是2017年中的时候,因为要搞深度学习的东西,就自学了斯坦福cs231n的神经网络的课。Youtube上有至少两期的公开课视频。好像从李飞飞离职之后,截止到2017年春季,就没再继续了。现在想想哪门课的内容挺多挺繁杂的。虽然是本科的课,最后好像每个学
- 向量对向量求导,链式法则
构建的乐趣
向量对向量求导
这还算不得向量微积分里多么主干的内容,只是一个小技术,但是数学推导很多时候就会用到。http://cs231n.stanford.edu/vecDerivs.pdf这个文献是一个好文献。另优秀翻译:https://zhuanlan.zhihu.com/p/142668996链式法则注意:这里的乘法变成了innerproduct推导过程中比较关键的点:除了利用这文献所讲的分量慢慢推,还有一个要点,首
- Win10上关于cs231n(2017)课后作业的环境配置
Diane小山
开始首先,这篇文章是针对那些想完成cs231n作业,但是觉得装linux双系统很麻烦的童鞋。cs231n作业的SetUp官方教程只针对了那些使用Unix(Ubuntu,Macos等)的人,对使用Windows的人十分不友好。安装anaconda百度一篇anaconda的安装教程,照着安装即可。这里需要提醒的有两点:国内的anaconda镜像能用的基本都挂了,所以还是老老实实去官方网站下载吧:)一定
- CS231N assignment2 SVM
weixin_30363509
数据结构与算法人工智能python
CS231NAssignment2SupportVectorMachineBegin本文主要介绍CS231N系列课程的第一项作业,写一个SVM无监督学习训练模型。课程主页:网易云课堂CS231N系列课程语言:Python3.61线形分类器以图像为例,一幅图像像素为32*32*3代表长32宽32有3通道的衣服图像,将其变为1*3072的一个向量,即该图像的特征向量。我们如果需要训练1000幅图像,那
- 【AI】斯坦福CS231n课程练习(1)—— KNN和SVM分类
李清焰
CS231nKNNSVM
文章目录一、前言1、CS231n是啥?2、本篇博客任务3、使用的数据集二、知识准备1、KNN是什么?2、SVM是什么?SVM的组成:三、实验——KNN和SVM分类1、KNN图片分类(重要步骤将在目录上体现)(1)在colab上切换目录,加载dataset(2)加载包、设置和外部模块(3)加载、初步处理数据(4)可视化打印一些图片看看我们的数据集长什么样(5)对测试、训练数据进行分组(6)创建KNN
- 深度学习系列之cs231n assignment1 KNN(二)
明曦君
深度学习python机器学习
写在前面:久经周折,终于能够将KNN系列给大家继续分享了,这次的内容来源于李飞飞教授团队的cs231n深度学习课程的作业1中的KNN研究,我会在全文我遇到困难的地方进行分享,以及一些想法。内容安排深度学习系列依托与cs231n的课程作业,因为只想练习编程,所以不对课程内容进行分享,仅针对编程内容进行分享。那么这一次的分享就是assignment1中K近邻分类器的使用,以及完成其中的四个问题,这四个
- cs231n assignment2(3)
没天赋的学琴
assignment2的第三部分,是熟悉深度学习框架pytorch或者tensorflow,这里选择的是使用pytorch框架。该部分主要通过三个层次:Barebones、ModuleAPI、SequentialAPI,来了解pytorch。Barebones在该层次中,需要利用pytorch所提供的一些函数,不仅需要定义神经网络的结构,同时还需编写网络的前向传播以及模型的训练部分;而参数的梯度可
- 第三十三周学习笔记
luputo
学习笔记
第三十三周学习笔记CS231nDeepLearningSoftwareCPUvsGPUCPU:Fewercores,buteachcoreismuchfasterandmuchmorecapable;greatatsequentialtasksGPU:Morecores,buteachcoreismuchslowerand“dumber”;greatforparalleltasks(matrixm
- CNN(卷积神经网络)、RNN(循环神经网络)、DNN,LSTM
weixin_34174132
人工智能
http://cs231n.github.io/neural-networks-1https://arxiv.org/pdf/1603.07285.pdfhttps://adeshpande3.github.io/adeshpande3.github.io/A-Beginner's-Guide-To-Understanding-Convolutional-Neural-Networks/Appli
- CNN笔记:通俗理解卷积神经网络
I_O_fly
神经网络cnn神经网络深度学习
通俗理解卷积神经网络(cs231n与5月dl班课程笔记)1前言2012年我在北京组织过8期machinelearning读书会,那时“机器学习”非常火,很多人都对其抱有巨大的热情。当我2013年再次来到北京时,有一个词似乎比“机器学习”更火,那就是“深度学习”。本博客内写过一些机器学习相关的文章,但上一篇技术文章“LDA主题模型”还是写于2014年11月份,毕竟自2015年开始创业做在线教育后,太
- Knn算法与 Svm算法对比
一个不知名的码农
支持向量机算法机器学习
Knn算法与Svm算法对比这里首先借用一个博主所做的图表,讲的很有理有据(7条消息)[cs231n]KNN与SVM区别_Rookie’Program的博客-CSDN博客_knn和svm的区别这里我们来讲一下我对这两个算法的理解knn看起来就是比较简单的一个数学模型,就是划范围论,精细程度实际上可能没有svm好,并且测试量也不能大,数据一大,处理起来又很麻烦,预测效率也比较低。相反的svm和knn对
- 斯坦福大学CS520知识图谱系列课程学习笔记:第一讲什么是知识图谱
ngl567
随着知识图谱在人工智能各个领域的广泛使用,知识图谱受到越来越多AI研究人员的关注和学习,已经成为人工智能迈向认知系统的关键技术之一。之前,斯坦福大学的面向计算机视觉的CS231n和面向自然语言处理的CS224n成为了全球非常多AI研究人员的入门经典学习课程。因此,斯坦福大学于今年3月开设了一门专门面向知识图谱的系列课程CS520,官网课程页:https://web.stanford.edu/cla
- 北京邮电大学 计算机视觉与深度学习 鲁鹏 计算机视觉概述课程手迹
qinyaoze
机器学习CV手记计算机视觉人工智能深度学习
课程笔记计算机视觉=输入(认知神经科学-理论,运用方法&算法,硬件)+输出(机器人)课程:图像处理-CS131,图像结构-CS231a,图像理论-CS230/CS231nQ-象棋与人工智能的关系?IBM-深蓝,Google-AlphaGo>>机器赢得象棋胜利=强大的搜索算法目标:语义鸿沟,即建立图像像素核语义间的关系发展过程:系统出现-物种大繁荣>>理论研究-猫视觉神经>>积木世界>>MIT图像处
- 国外AI大牛推荐的10大最有帮助免费在线机器学习课程
机器学习与系统
woman_ml.jpg本文编译自twitter用户chipro斯坦福在线自学课程《概率与统计》:该课程涉及概率统计的基本概念,涵盖机器学习4个基本方面:探索性数据分析,产生数据,概率和推理。MIT的《线性代数》:这是我见过的最好的线性代数课程,由传奇教授GilbertStrang(吉尔伯特斯特朗)教授。斯坦福的CS231N:用于视觉识别的卷积神经网络:平衡理论与实践。课堂笔记写得很好,解释了不同
- CS231n学习笔记--计算机视觉历史回顾与介绍1
听城
CS231n简介首先我们来看看官方对这门课的介绍:计算机视觉在社会中已经逐渐普及,并广泛运用于搜索检索、图像理解、手机应用、地图导航、医疗制药、无人机和无人驾驶汽车等领域。而这些应用的核心技术就是图像分类、图像定位和图像探测等视觉识别任务。近期神经网络(也就是“深度学习”)方法上的进展极大地提升了这些代表当前发展水平的视觉识别系统的性能。本课程将深入讲解深度学习框架的细节问题,聚焦面向视觉识别任务
- 计算机视觉实战项目(图像分类+目标检测+目标跟踪+姿态识别+车道线识别+车牌识别)
阿利同学
计算机视觉分类目标检测
图像分类教程博客_传送门链接:链接在本教程中,您将学习如何使用迁移学习训练卷积神经网络以进行图像分类。您可以在cs231n上阅读有关迁移学习的更多信息。本文主要目的是教会你如何自己搭建分类模型,耐心看完,相信会有很大收获。废话不多说,直切主题…首先们要知道深度学习大都包含了下面几个方面:1.加载(处理)数据2.网络搭建3.损失函数(模型优化)4模型训练和保存把握好这些主要内容和流程,基本上对分类模
- cs231n assignment2(2)
没天赋的学琴
assignment2的第二部分的内容,实现一个卷积神经网络。这一部分主要是实现卷积神经网络中的一些所需用到的layer类型:卷积层(convolution)和池化层(这里是实现max-pooling)。这部分的实现是不考虑其运行效率,而在真正的实现应用上,卷积神经网络的运行效率是一个很重要的问题。卷积层卷积层是由一个个过滤器(filter),每个过滤器的尺寸为:,这里的的大小与输入的图像或act
- cs231n作业:Assignment1-Softmax
Diane小山
softmax.pydefsoftmax_loss_naive(W,X,y,reg):"""Softmaxlossfunction,naiveimplementation(withloops)InputshavedimensionD,thereareCclasses,andweoperateonminibatchesofNexamples.Inputs:-W:Anumpyarrayofshape(
- LeetCode[Math] - #66 Plus One
Cwind
javaLeetCode题解AlgorithmMath
原题链接:#66 Plus One
要求:
给定一个用数字数组表示的非负整数,如num1 = {1, 2, 3, 9}, num2 = {9, 9}等,给这个数加上1。
注意:
1. 数字的较高位存在数组的头上,即num1表示数字1239
2. 每一位(数组中的每个元素)的取值范围为0~9
难度:简单
分析:
题目比较简单,只须从数组
- JQuery中$.ajax()方法参数详解
AILIKES
JavaScriptjsonpjqueryAjaxjson
url: 要求为String类型的参数,(默认为当前页地址)发送请求的地址。
type: 要求为String类型的参数,请求方式(post或get)默认为get。注意其他http请求方法,例如put和 delete也可以使用,但仅部分浏览器支持。
timeout: 要求为Number类型的参数,设置请求超时时间(毫秒)。此设置将覆盖$.ajaxSetup()方法的全局
- JConsole & JVisualVM远程监视Webphere服务器JVM
Kai_Ge
JVisualVMJConsoleWebphere
JConsole是JDK里自带的一个工具,可以监测Java程序运行时所有对象的申请、释放等动作,将内存管理的所有信息进行统计、分析、可视化。我们可以根据这些信息判断程序是否有内存泄漏问题。
使用JConsole工具来分析WAS的JVM问题,需要进行相关的配置。
首先我们看WAS服务器端的配置.
1、登录was控制台https://10.4.119.18
- 自定义annotation
120153216
annotation
Java annotation 自定义注释@interface的用法 一、什么是注释
说起注释,得先提一提什么是元数据(metadata)。所谓元数据就是数据的数据。也就是说,元数据是描述数据的。就象数据表中的字段一样,每个字段描述了这个字段下的数据的含义。而J2SE5.0中提供的注释就是java源代码的元数据,也就是说注释是描述java源
- CentOS 5/6.X 使用 EPEL YUM源
2002wmj
centos
CentOS 6.X 安装使用EPEL YUM源1. 查看操作系统版本[root@node1 ~]# uname -a Linux node1.test.com 2.6.32-358.el6.x86_64 #1 SMP Fri Feb 22 00:31:26 UTC 2013 x86_64 x86_64 x86_64 GNU/Linux [root@node1 ~]#
- 在SQLSERVER中查找缺失和无用的索引SQL
357029540
SQL Server
--缺失的索引
SELECT avg_total_user_cost * avg_user_impact * ( user_scans + user_seeks ) AS PossibleImprovement ,
last_user_seek ,
- Spring3 MVC 笔记(二) —json+rest优化
7454103
Spring3 MVC
接上次的 spring mvc 注解的一些详细信息!
其实也是一些个人的学习笔记 呵呵!
- 替换“\”的时候报错Unexpected internal error near index 1 \ ^
adminjun
java“\替换”
发现还是有些东西没有刻子脑子里,,过段时间就没什么概念了,所以贴出来...以免再忘...
在拆分字符串时遇到通过 \ 来拆分,可是用所以想通过转义 \\ 来拆分的时候会报异常
public class Main {
/*
- POJ 1035 Spell checker(哈希表)
aijuans
暴力求解--哈希表
/*
题意:输入字典,然后输入单词,判断字典中是否出现过该单词,或者是否进行删除、添加、替换操作,如果是,则输出对应的字典中的单词
要求按照输入时候的排名输出
题解:建立两个哈希表。一个存储字典和输入字典中单词的排名,一个进行最后输出的判重
*/
#include <iostream>
//#define
using namespace std;
const int HASH =
- 通过原型实现javascript Array的去重、最大值和最小值
ayaoxinchao
JavaScriptarrayprototype
用原型函数(prototype)可以定义一些很方便的自定义函数,实现各种自定义功能。本次主要是实现了Array的去重、获取最大值和最小值。
实现代码如下:
<script type="text/javascript">
Array.prototype.unique = function() {
var a = {};
var le
- UIWebView实现https双向认证请求
bewithme
UIWebViewhttpsObjective-C
什么是HTTPS双向认证我已在先前的博文 ASIHTTPRequest实现https双向认证请求
中有讲述,不理解的读者可以先复习一下。本文是用UIWebView来实现对需要客户端证书验证的服务请求,网上有些文章中有涉及到此内容,但都只言片语,没有讲完全,更没有完整的代码,让人困扰不已。但是此知
- NoSQL数据库之Redis数据库管理(Redis高级应用之事务处理、持久化操作、pub_sub、虚拟内存)
bijian1013
redis数据库NoSQL
3.事务处理
Redis对事务的支持目前不比较简单。Redis只能保证一个client发起的事务中的命令可以连续的执行,而中间不会插入其他client的命令。当一个client在一个连接中发出multi命令时,这个连接会进入一个事务上下文,该连接后续的命令不会立即执行,而是先放到一个队列中,当执行exec命令时,redis会顺序的执行队列中
- 各数据库分页sql备忘
bingyingao
oraclesql分页
ORACLE
下面这个效率很低
SELECT * FROM ( SELECT A.*, ROWNUM RN FROM (SELECT * FROM IPAY_RCD_FS_RETURN order by id desc) A ) WHERE RN <20;
下面这个效率很高
SELECT A.*, ROWNUM RN FROM (SELECT * FROM IPAY_RCD_
- 【Scala七】Scala核心一:函数
bit1129
scala
1. 如果函数体只有一行代码,则可以不用写{},比如
def print(x: Int) = println(x)
一行上的多条语句用分号隔开,则只有第一句属于方法体,例如
def printWithValue(x: Int) : String= println(x); "ABC"
上面的代码报错,因为,printWithValue的方法
- 了解GHC的factorial编译过程
bookjovi
haskell
GHC相对其他主流语言的编译器或解释器还是比较复杂的,一部分原因是haskell本身的设计就不易于实现compiler,如lazy特性,static typed,类型推导等。
关于GHC的内部实现有篇文章说的挺好,这里,文中在RTS一节中详细说了haskell的concurrent实现,里面提到了green thread,如果熟悉Go语言的话就会发现,ghc的concurrent实现和Go有点类
- Java-Collections Framework学习与总结-LinkedHashMap
BrokenDreams
LinkedHashMap
前面总结了java.util.HashMap,了解了其内部由散列表实现,每个桶内是一个单向链表。那有没有双向链表的实现呢?双向链表的实现会具备什么特性呢?来看一下HashMap的一个子类——java.util.LinkedHashMap。
- 读《研磨设计模式》-代码笔记-抽象工厂模式-Abstract Factory
bylijinnan
abstract
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
package design.pattern;
/*
* Abstract Factory Pattern
* 抽象工厂模式的目的是:
* 通过在抽象工厂里面定义一组产品接口,方便地切换“产品簇”
* 这些接口是相关或者相依赖的
- 压暗面部高光
cherishLC
PS
方法一、压暗高光&重新着色
当皮肤很油又使用闪光灯时,很容易在面部形成高光区域。
下面讲一下我今天处理高光区域的心得:
皮肤可以分为纹理和色彩两个属性。其中纹理主要由亮度通道(Lab模式的L通道)决定,色彩则由a、b通道确定。
处理思路为在保持高光区域纹理的情况下,对高光区域着色。具体步骤为:降低高光区域的整体的亮度,再进行着色。
如果想简化步骤,可以只进行着色(参看下面的步骤1
- Java VisualVM监控远程JVM
crabdave
visualvm
Java VisualVM监控远程JVM
JDK1.6开始自带的VisualVM就是不错的监控工具.
这个工具就在JAVA_HOME\bin\目录下的jvisualvm.exe, 双击这个文件就能看到界面
通过JMX连接远程机器, 需要经过下面的配置:
1. 修改远程机器JDK配置文件 (我这里远程机器是linux).
- Saiku去掉登录模块
daizj
saiku登录olapBI
1、修改applicationContext-saiku-webapp.xml
<security:intercept-url pattern="/rest/**" access="IS_AUTHENTICATED_ANONYMOUSLY" />
<security:intercept-url pattern=&qu
- 浅析 Flex中的Focus
dsjt
htmlFlexFlash
关键字:focus、 setFocus、 IFocusManager、KeyboardEvent
焦点、设置焦点、获得焦点、键盘事件
一、无焦点的困扰——组件监听不到键盘事件
原因:只有获得焦点的组件(确切说是InteractiveObject)才能监听到键盘事件的目标阶段;键盘事件(flash.events.KeyboardEvent)参与冒泡阶段,所以焦点组件的父项(以及它爸
- Yii全局函数使用
dcj3sjt126com
yii
由于YII致力于完美的整合第三方库,它并没有定义任何全局函数。yii中的每一个应用都需要全类别和对象范围。例如,Yii::app()->user;Yii::app()->params['name'];等等。我们可以自行设定全局函数,使得代码看起来更加简洁易用。(原文地址)
我们可以保存在globals.php在protected目录下。然后,在入口脚本index.php的,我们包括在
- 设计模式之单例模式二(解决无序写入的问题)
come_for_dream
单例模式volatile乱序执行双重检验锁
在上篇文章中我们使用了双重检验锁的方式避免懒汉式单例模式下由于多线程造成的实例被多次创建的问题,但是因为由于JVM为了使得处理器内部的运算单元能充分利用,处理器可能会对输入代码进行乱序执行(Out Of Order Execute)优化,处理器会在计算之后将乱序执行的结果进行重组,保证该
- 程序员从初级到高级的蜕变
gcq511120594
框架工作PHPandroidhtml5
软件开发是一个奇怪的行业,市场远远供不应求。这是一个已经存在多年的问题,而且随着时间的流逝,愈演愈烈。
我们严重缺乏能够满足需求的人才。这个行业相当年轻。大多数软件项目是失败的。几乎所有的项目都会超出预算。我们解决问题的最佳指导方针可以归结为——“用一些通用方法去解决问题,当然这些方法常常不管用,于是,唯一能做的就是不断地尝试,逐个看看是否奏效”。
现在我们把淫浸代码时间超过3年的开发人员称为
- Reverse Linked List
hcx2013
list
Reverse a singly linked list.
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
p
- Spring4.1新特性——数据库集成测试
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- C# Ajax上传图片同时生成微缩图(附Demo)
liyonghui160com
1.Ajax无刷新上传图片,详情请阅我的这篇文章。(jquery + c# ashx)
2.C#位图处理 System.Drawing。
3.最新demo支持IE7,IE8,Fir
- Java list三种遍历方法性能比较
pda158
java
从c/c++语言转向java开发,学习java语言list遍历的三种方法,顺便测试各种遍历方法的性能,测试方法为在ArrayList中插入1千万条记录,然后遍历ArrayList,发现了一个奇怪的现象,测试代码例如以下:
package com.hisense.tiger.list;
import java.util.ArrayList;
import java.util.Iterator;
- 300个涵盖IT各方面的免费资源(上)——商业与市场篇
shoothao
seo商业与市场IT资源免费资源
A.网站模板+logo+服务器主机+发票生成
HTML5 UP:响应式的HTML5和CSS3网站模板。
Bootswatch:免费的Bootstrap主题。
Templated:收集了845个免费的CSS和HTML5网站模板。
Wordpress.org|Wordpress.com:可免费创建你的新网站。
Strikingly:关注领域中免费无限的移动优
- localStorage、sessionStorage
uule
localStorage
W3School 例子
HTML5 提供了两种在客户端存储数据的新方法:
localStorage - 没有时间限制的数据存储
sessionStorage - 针对一个 session 的数据存储
之前,这些都是由 cookie 完成的。但是 cookie 不适合大量数据的存储,因为它们由每个对服务器的请求来传递,这使得 cookie 速度很慢而且效率也不