深度学习进阶:自然语言处理入门:第2章 自然语言和单词的分布式表示
深度学习进阶:自然语言处理入门
- 第2章 自然语言和单词的分布式表示
-
- 2.1 什么是自然语言处理
-
- 单词含义
- 2.2 同义词词典
-
- 2.2.1 WordNet
- 2.2.2 同义词词典的问题
- 2.3 基于计数的方法(*)
-
- 2.3.1 基于 Python的语料库的预处理
-
- 语料库的准备工作 ,处理实现为 preprocess() 函数
- 2.3.2 单词的分布式表示
- 2.3.3 分布式假设
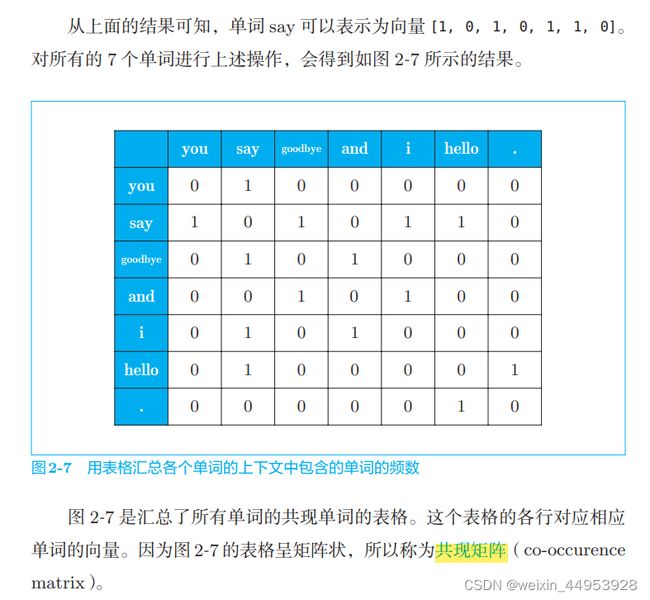
- 2.3.4 共现矩阵
-
- 共现矩阵的函数: create_co_matrix(corpus, vocab_size, window_size=1)
- 2.3.5 向量间的相似度
-
- cos_similarity(x, y, eps=1e-8)
- 求得单词向量间的相似度
- 2.3.6 相似单词的排序
-
- most_similar() 函数:降序输出
- 执行函数
- 2.4 基于计数的方法的改进
-
- 2.4.1 点互信息
-
- 共现矩阵转化为 PPMI 矩阵的函数。
- 执行函数
- 2.4.2 降维
- 2.4.3 基于 SVD的降维
- 2.4.4 PTB数据集
- 2.4.5 基于 PTB数据集的评价
- 2.5 小结
- 本章所学的内容
第2章 自然语言和单词的分布式表示
自然语言处理涉及多个子 领域,但是它们的根本任务都是让计算机理解我们的语言。
我们将先详细考察古典方法,即深度学习出现以前的方法。从下一章开 始,再介绍基于深度学习(确切地说,是神经网络)的方法。
本章我们还会练习使用 Python 处理文本,实现分词(将文本分割成单 词)和单词 ID 化(将单词转换为单词 ID)等任务。本章实现的函数在后 面的章节中也会用到。因此,本章也可以说是后续文本处理的准备工作。
2.1 什么是自然语言处理
自然语言处理(Natural Language Processing,NLP),顾名思义,就是处理自然语言的科学。简单地说,它是一种能够让计算机理解人类语言的 技术。换言之,自然语言处理的目标就是让计算机理解人说的话,进而完成对我们有帮助的事情
单词含义
本章的主题是让计算机理解单词含义。确切地说,我们将探讨一些巧 妙地蕴含了单词含义的表示方法。具体来说,本章和下一章将讨论以下 3 种 方法。
- 基于同义词词典的方法 本章
- 基于计数的方法 本章
- 基于推理的方法(word2vec) 下一章
首先,我们将简单介绍一下使用人工整理好的同义词词典的方法。然 后,对利用统计信息表示单词的方法(这里称为“基于计数的方法”)进行说 明。这些都是本章学习的内容。在下一章,我们将讨论利用神经网络的基于 推理的方法(具体来说,就是 word2vec 方法)。
2.2 同义词词典
在同义词词典中,具有相同含义的单词(同义词)或含义类似的单词(近义词)被归 类到同一个组中。比如,使用同义词词典,我们可以知道 car 的同义词有 automobile、motorcar 等(图 2-1)
2.2.1 WordNet
在自然语言处理领域,最著名的同义词词典是WordNet。WordNet 是普林斯顿大学于 1985 年开始开发的同义词词典,
使用 WordNet,可以获得单词的近义词,或者利用单词网络。使用单 词网络,可以计算单词之间的相似度。
2.2.2 同义词词典的问题
WordNet 等同义词词典中对大量单词定义了同义词和层级结构关系等。 利用这些知识,可以(间接地)让计算机理解单词含义。不过,人工标记也 存在一些较大的缺陷。下面,我们就来看一下同义词词典的主要问题,并分 别对其进行简要说明。
-
难以顺应时代变化
-
人力成本高
-
无法表示单词的微妙差异
2.3 基于计数的方法(*)
从介绍基于计数的方法开始,我们将使用语料库(corpus)
**语料库就是大量的文本数据。**不过,语料库并不是胡乱收集数据,一般收集 的都是用于自然语言处理研究和应用的文本数据。
自然语言处理领域中使用的语料库有时会给文本数据添加额外的信息。比如,可以给文本数据的各个单词标记词性。在这种情况 下,为了方便计算机处理,语料库通常会被结构化(比如,采用树结构等数据形式)。这里,假定我们使用的语料库没有添加标签, 而是作为一个大的文本文件,只包含简单的文本数据。
2.3.1 基于 Python的语料库的预处理
自然语言处理领域存在各种各样的语料库。说到有名的语料库,有 Wikipedia 和 Google News 等。本章我们先使用仅包含一个句子的简单文本作为语 料库,然后再处理更实用的语料库。
text = 'You say goodbye and I say hello.'
text = text.lower() #使用 lower() 方法将所有字母转化为小写
text = text.replace('.', ' .') #我们先在句号前插入一个空格(即用“ .”替换“.”)
text #'you say goodbye and i say hello .'
words = text.split(' ') #进行分词。
words #['you', 'say', 'goodbye', 'and', 'i', 'say', 'hello', '.']
word_to_id = {}
id_to_word = {}
for word in words:
if word not in word_to_id:
new_id = len(word_to_id)
word_to_id[word] = new_id
id_to_word[new_id] = word
import numpy as np
corpus = [word_to_id[w] for w in words]
corpus = np.array(corpus)
corpus #array([0, 1, 2, 3, 4, 1, 5, 6])
这里,在进行分词时,我们采用了一种在句号前插入空格的 “临 时 对 策”,其 实 还 有 更 加 聪 明、更 加 通 用 的 实 现 方 式,比 如 使 用 正 则 表 达 式。通 过 导 入 正 则 表 达 式 的 re 模 块,使 用 re.split(’(\W+)?’, text)也可以进行分词。
变量 id_to_word 负责将单词 ID 转化为单词(键是单词 ID,值是单词),word_to_id 负责将单词转化为单词 ID。
这里,我们从头开始逐一观察分词后 的 words 的各个元素,如果单词不在 word_to_id 中,则分别向 word_to_id 和 id_to_word 添加新 ID 和单词。另外,我们将字典的长度设为新的单词 ID, 单词 ID 按 0, 1, 2, ··· 逐渐增加
id_to_word #{0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6: '.'}
word_to_id # {'you': 0, 'say': 1, 'goodbye': 2, 'and': 3, 'i': 4, 'hello': 5, '.': 6})
id_to_word[1] #'say'
word_to_id['hello'] #5
最后,我们将单词列表转化为单词 ID 列表。这里,我们使用 Python 的列表解析式将单词列表转化为单词 ID 列表,然后再将其转化为 NumPy 数组。
列表解析式(list comprehension)或字典解析式(dict comprehension) 是一种便于对列表或字典进行循环处理的写法。比如,要创建元素为列表 xs = [1,2,3,4]中各个元素的平方的新列表,可以写成 [x**2 for x in xs]。
xs = [1,2,3,4]
xs=[a**2 for a in xs]
xs #[1, 4, 9, 16]
xs=np.array(xs)
xs #array([ 1, 4, 9, 16]) #然后再将其转化为 NumPy数组。
语料库的准备工作 ,处理实现为 preprocess() 函数
def preprocess(text):
text = text.lower()
text = text.replace('.', ' .')
words = text.split(' ')
word_to_id = {}
id_to_word = {}
for word in words:
if word not in word_to_id:
new_id = len(word_to_id)
word_to_id[word] = new_id
id_to_word[new_id] = word
corpus = np.array([word_to_id[w] for w in words])
return corpus, word_to_id, id_to_word
使用这个函数,可以按如下方式对语料库进行预处理
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
corpus #array([0, 1, 2, 3, 4, 1, 5, 6])
word_to_id #{'you': 0, 'say': 1, 'goodbye': 2, 'and': 3, 'i': 4, 'hello': 5, '.': 6}
id_to_word # {0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6: '.'}
2.3.2 单词的分布式表示
单词的分布式表示将单词表示为固定长度的向量。这种向量的特 征在于它是用密集向量表示的。密集向量的意思是,向量的各个 元 素(大 多 数)是 由 非 0 实数表示的。例如,三维分布式表示是 [0.21,-0.45,0.83]。如何构建这样的单词的分布式表示是我们接下 来的一个重要课题。
2.3.3 分布式假设
在自然语言处理的历史中,用向量表示单词的研究有很多。如果仔 细看一下这些研究,就会发现几乎所有的重要方法都基于一个简单的想 法,这个想法就是“某个单词的含义由它周围的单词形成”,称为分布式假设(distributional hypothesis)
2.3.4 共现矩阵
import sys
sys.path.append('..')
import numpy as np
from common.util import preprocess
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
print(corpus)
# [0 1 2 3 4 1 5 6]
print(id_to_word)
# {0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6: '.'}
C = np.array([
[0, 1, 0, 0, 0, 0, 0],
[1, 0, 1, 0, 1, 1, 0],
[0, 1, 0, 1, 0, 0, 0],
[0, 0, 1, 0, 1, 0, 0],
[0, 1, 0, 1, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 1, 0],
], dtype=np.int32)
print(C[0]) # 单词ID为0的向量
# [0 1 0 0 0 0 0]
print(C[4]) # 单词ID为4的向量
# [0 1 0 1 0 0 0]
print(C[word_to_id['goodbye']]) # goodbye的向量
# [0 1 0 1 0 0 0]
共现矩阵的函数: create_co_matrix(corpus, vocab_size, window_size=1)
其中参数 corpus 是单词 ID 列表,参数 vocab_ size 是词汇个数,window_size 是窗口大小
def create_co_matrix(corpus, vocab_size, window_size=1):
'''生成共现矩阵
:param corpus: 语料库(单词ID列表)
:param vocab_size:词汇个数,重复的单词算成一个
:param window_size:窗口大小(当窗口大小为1时,左右各1个单词为上下文)
:return: 共现矩阵
'''
corpus_size = len(corpus) #单词总数,包括重度的单词
co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)
for idx, word_id in enumerate(corpus):
for i in range(1, window_size + 1):
left_idx = idx - i
right_idx = idx + i
if left_idx >= 0:
left_word_id = corpus[left_idx]
co_matrix[word_id, left_word_id] += 1
if right_idx < corpus_size:
right_word_id = corpus[right_idx]
co_matrix[word_id, right_word_id] += 1
return co_matrix
首先,用元素为 0 的二维数组对 co_matrix 进行初始化。然后,针对语 料库中的每一个单词,计算它的窗口中包含的单词。同时,检查窗口内的单 词是否超出了语料库的左端和右端
2.3.5 向量间的相似度
cos_similarity(x, y, eps=1e-8)
def cos_similarity(x, y, eps=1e-8):
nx = x / (np.sqrt(np.sum(x ** 2)) + eps) # x的正规化
ny = y / (np.sqrt(np.sum(y ** 2)) + eps) # y的正规化
return np.dot(nx, ny)
首先对向量进行正规化, 然后求两个向量的内积
在执行除法时加上一个微小值。这 里,通过参数指定一个微小值 eps(eps 是 epsilon 的缩写),并默认 eps=1e-8 (= 0.000 000 01)
求得单词向量间的相似度
import sys
sys.path.append('..')
from common.util import preprocess, create_co_matrix, cos_similarity
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)
c0 = C[word_to_id['you']] #you的单词向量
c1 = C[word_to_id['i']] #iの单词向量
print(cos_similarity(c0, c1))
#0.7071067691154799
从上面的结果可知,you 和 i 的余弦相似度是 0.70 …。由于余弦相似度 的取值范围是 −1 到 1,所以可以说这个值是相对比较高的(存在相似性)
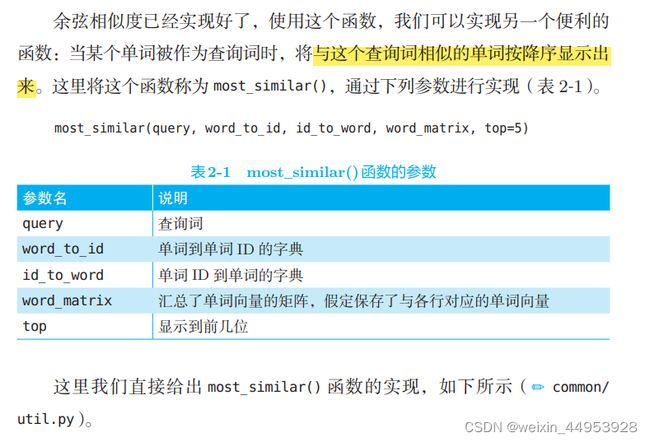
2.3.6 相似单词的排序
most_similar() 函数:降序输出
def most_similar(query, word_to_id, id_to_word, word_matrix, top=5):
'''相似单词的查找
:param query: 查询词
:param word_to_id: 从单词到单词ID的字典
:param id_to_word: 从单词ID到单词的字典
:param word_matrix: 汇总了单词向量的矩阵,假定保存了与各行对应的单词向量
:param top: 显示到前几位
'''
if query not in word_to_id:
print('%s is not found' % query)
return
print('\n[query] ' + query)
query_id = word_to_id[query]
query_vec = word_matrix[query_id]
vocab_size = len(id_to_word) #7
similarity = np.zeros(vocab_size) #array([0., 0., 0., 0., 0., 0., 0.])
for i in range(vocab_size):
similarity[i] = cos_similarity(word_matrix[i], query_vec)
count = 0
for i in (-1 * similarity).argsort():
if id_to_word[i] == query:
continue
print(' %s: %s' % (id_to_word[i], similarity[i]))
count += 1
if count >= top:
return
上述实现按如下顺序执行。
❶ 取出查询词的单词向量。
❷ 分别求得查询词的单词向量和其他所有单词向量的余弦相似度。
❸ 基于余弦相似度的结果,按降序显示它们的值。
执行函数
import sys
sys.path.append('..')
from common.util import preprocess, create_co_matrix, most_similar
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)
most_similar('you', word_to_id, id_to_word, C, top=5)
输出
[query] you
goodbye: 0.7071067691154799
i: 0.7071067691154799
hello: 0.7071067691154799
say: 0.0
and: 0.0
2.4 基于计数的方法的改进
2.4.1 点互信息
上一节的共现矩阵的元素表示两个单词同时出现的次数。但是,这种 “原始”的次数并不具备好的性质。

其中,P(x) 表示 x 发生的概率,P(y) 表示 y 发生的概率,P(x, y) 表示 x 和 y 同时发生的概率。PMI 的值越高,表明相关性越强


共现矩阵转化为 PPMI 矩阵的函数。
def ppmi(C, verbose=False, eps = 1e-8):
'''生成PPMI(正的点互信息)
:param C: 共现矩阵
:param verbose: 是否输出进展情况
:return:
'''
M = np.zeros_like(C, dtype=np.float32)
N = np.sum(C)
S = np.sum(C, axis=0)
total = C.shape[0] * C.shape[1]
cnt = 0
for i in range(C.shape[0]):
for j in range(C.shape[1]):
pmi = np.log2(C[i, j] * N / (S[j]*S[i]) + eps)
M[i, j] = max(0, pmi)
if verbose:
cnt += 1
if cnt % (total//100 + 1) == 0:
print('%.1f%% done' % (100*cnt/total))
return M
verbose 是决定是否输出运行情况的标志。 当处理大语料库时,设置 verbose=True,可以用于确认运行情况。在这段代码 中,为了仅从共现矩阵求 PPMI 矩阵而进行了简单的实现。
import numpy as np
C = np.array([
[0, 1, 0, 0, 0, 0, 1],
[1, 0, 1, 0, 1, 1, 0],
[0, 1, 0, 1, 0, 0, 0],
[0, 0, 1, 0, 1, 0, 0],
[0, 1, 0, 1, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 1, 0],
], dtype=np.int32)
N = np.sum(C) #15
S = np.sum(C, axis=0) #array([1, 4, 2, 2, 2, 2, 2])
执行函数
import sys
sys.path.append('..')
import numpy as np
from common.util import preprocess, create_co_matrix, cos_similarity, ppmi
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)
W = ppmi(C)
np.set_printoptions(precision=3) # 有效位数为3位
print('covariance matrix')
print(C)
print('-'*50)
print('PPMI')
print(W)
输出
covariance matrix
[[0 1 0 0 0 0 0]
[1 0 1 0 1 1 0]
[0 1 0 1 0 0 0]
[0 0 1 0 1 0 0]
[0 1 0 1 0 0 0]
[0 1 0 0 0 0 1]
[0 0 0 0 0 1 0]]
--------------------------------------------------
PPMI
[[0. 1.807 0. 0. 0. 0. 0. ]
[1.807 0. 0.807 0. 0.807 0.807 0. ]
[0. 0.807 0. 1.807 0. 0. 0. ]
[0. 0. 1.807 0. 1.807 0. 0. ]
[0. 0.807 0. 1.807 0. 0. 0. ]
[0. 0.807 0. 0. 0. 0. 2.807]
[0. 0. 0. 0. 0. 2.807 0. ]]
Process finished with exit code 0
PPMI 矩 阵的各个元素均为大于等于 0 的实数。我们得到了一个由更好的指标形成的 矩阵,这相当于获取了一个更好的单词向量。
但是,这个 PPMI 矩阵还是存在一个很大的问题,那就是随着语料库 的词汇量增加,各个单词向量的维数也会增加。如果语料库的词汇量达到 10 万,则单词向量的维数也同样会达到 10 万。实际上,处理 10 万维向量 是不现实的。
2.4.2 降维
所谓降维(dimensionality reduction),顾名思义,就是减少向量维度。 但是,并不是简单地减少,而是在尽量保留“重要信息”的基础上减少。
向量中的大多数元素为 0 的矩阵(或向量)称为稀疏矩阵(或稀疏向 量)。这里的重点是,从稀疏向量中找出重要的轴,用更少的维度对 其进行重新表示。结果,稀疏矩阵就会被转化为大多数元素均不为 0 的密集矩阵。这个密集矩阵就是我们想要的单词的分布式表示。


单词的共现矩阵是正方形矩阵,但在图 2-10 中,为了和之前的 图一致,画的是长方形。另外,这里对 SVD 的介绍仅限于最直 观的概要性的说明。
2.4.3 基于 SVD的降维
接下来,我们使用 Python 来实现 SVD,这里可以使用 NumPy 的 linalg 模块中的 svd 方法。linalg 是 linear algebra(线性代数)的简称。下 面,我们创建一个共现矩阵,将其转化为 PPMI 矩阵,然后对其进行 SVD
import sys
sys.path.append('..')
import numpy as np
import matplotlib.pyplot as plt
from common.util import preprocess, create_co_matrix, ppmi
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(id_to_word)
C = create_co_matrix(corpus, vocab_size, window_size=1)
W = ppmi(C)
# SVD
U, S, V = np.linalg.svd(W)
np.set_printoptions(precision=3) # 有效位数为3位
# 共现矩阵
print(C[0]) # [0 1 0 0 0 0 0]
# PPMI矩阵
print(W[0]) #[0. 1.807 0. 0. 0. 0. 0. ]
# SVD
print(U[0]) #[-3.409e-01 -1.110e-16 -3.886e-16 -1.205e-01 0.000e+00 9.323e-012.226e-16]
# plot
for word, word_id in word_to_id.items():
plt.annotate(word, (U[word_id, 0], U[word_id, 1]))
plt.scatter(U[:,0], U[:,1], alpha=0.5)
plt.show()
原先的稀疏向量 W[0] 经过 SVD 被转化成了密集向量 U[0]。如果要对这个密集向量降维,比如把它降维到二维向量,取出前两个元素 即可。
print(U[0, :2])
# [ 3.409e-01 -1.110e-16]
2.4.4 PTB数据集
PTB 语料库经常被用作评价提案方法的基准。本书中我们将使用 PTB 语料库进行各种实验。
我们使用的 PTB 语料库在 word2vec 的发明者托马斯·米科洛夫 (Tomas Mikolov)的网页上有提供。这个 PTB 语料库是以文本文件的形式 提供的,与原始的 PTB 的文章相比,多了若干预处理,包括将稀有单词替 换成特殊字符 (unk 是 unknown 的简称),将具体的数字替换成“N” 等。
在 PTB 语料库中,一行保存一个句子。
在本书中,为了方便使用 Penn Treebank 数据集,我们准备了专门 的 Python 代码。这个文件在 dataset/ptb.py 中,并假定从章节目录(ch01、 ch02、…)使用。比如,我们将当前目录移到 ch02 目录,并在这个目录中调用 python show_ptb.py。使用 ptb.py 的例子如下所示( ch02/show_ptb.py)
import sys
sys.path.append('..')
from dataset import ptb
corpus, word_to_id, id_to_word = ptb.load_data('train') #使用 ptb.load_data() 加载数据
print('corpus size:', len(corpus))
print('corpus[:30]:', corpus[:30])
print()
print('id_to_word[0]:', id_to_word[0])
print('id_to_word[1]:', id_to_word[1])
print('id_to_word[2]:', id_to_word[2])
print()
print("word_to_id['car']:", word_to_id['car'])
print("word_to_id['happy']:", word_to_id['happy'])
print("word_to_id['lexus']:", word_to_id['lexus'])
输出
corpus size: 929589
corpus[:30]: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29]
id_to_word[0]: aer
id_to_word[1]: banknote
id_to_word[2]: berlitz
word_to_id['car']: 3856
word_to_id['happy']: 4428
word_to_id['lexus']: 7426
Process finished with exit code 0
corpus 中保存了单词 ID 列表,id_to_word 是 将单词 ID 转化为单词的字典,word_to_id 是将单词转化为单词 ID 的字典。
使用 ptb.load_data() 加载数据。此时,指定参 数 ‘train’、‘test’ 和 ‘valid’ 中的一个,它们分别对应训练用数据、测试用 数据和验证用数据中的一个。以上就是 ptb.py 文件的使用方法。
2.4.5 基于 PTB数据集的评价
下面,我们将基于计数的方法应用于 PTB 数据集。这里建议使用更快 速的 SVD 对大矩阵执行 SVD,为此我们需要安装 sklearn 模块。当然,虽 然仍可以使用基本版的 SVD(np.linalg.svd()),但是这需要更多的时间和 内存。
import sys
sys.path.append('..')
import numpy as np
from common.util import most_similar, create_co_matrix, ppmi
from dataset import ptb
window_size = 2
wordvec_size = 100
corpus, word_to_id, id_to_word = ptb.load_data('train')
vocab_size = len(word_to_id)
print('counting co-occurrence ...')
#获取共享矩阵
C = create_co_matrix(corpus, vocab_size, window_size)
print('calculating PPMI ...')
# PPMI矩阵
W = ppmi(C, verbose=True)
print('calculating SVD ...')
try:
# truncated SVD (fast!)
#使用了 sklearn 的 randomized_svd() 方法
from sklearn.utils.extmath import randomized_svd
U, S, V = randomized_svd(W, n_components=wordvec_size, n_iter=5,
random_state=None)
except ImportError:
# SVD (slow)
U, S, V = np.linalg.svd(W)
word_vecs = U[:, :wordvec_size]
querys = ['you', 'year', 'car', 'toyota']
for query in querys:
most_similar(query, word_to_id, id_to_word, word_vecs, top=5)
我们使用了 sklearn 的 randomized_svd() 方法。 该方法通过使用了随机数的 Truncated SVD,仅对奇异值较大的部分进行 计算,计算速度比常规的 SVD 快。剩余的代码和之前使用小语料库时的代码差不太多。
输出
[query] you
i: 0.7282394170761108
we: 0.6513379216194153
anybody: 0.6080119609832764
do: 0.5862394571304321
something: 0.5007873773574829
[query] year
quarter: 0.6597371697425842
earlier: 0.6314752101898193
last: 0.6304394006729126
next: 0.6258531808853149
month: 0.6106938719749451
[query] car
luxury: 0.6737791299819946
auto: 0.6297322511672974
cars: 0.5983448028564453
corsica: 0.5530043244361877
vehicle: 0.5418606996536255
[query] toyota
motors: 0.7333338260650635
motor: 0.7045522332191467
nissan: 0.6448380947113037
lexus: 0.6417834758758545
mazda: 0.6350786089897156
Process finished with exit code 0
我们终于成功地将单词含义编码成了向量,真是可喜可贺!使用语料 库,计算上下文中的单词数量,将它们转化 PPMI 矩阵,再基于 SVD 降维 获得好的单词向量。这就是单词的分布式表示,每个单词表示为固定长度的 密集向量。
2.5 小结
本章,我们以自然语言为对象,特别是以让计算机理解单词含义为主题 展开了讨论。为了达到这一目标,我们介绍了基于同义词词典的方法,也考 察了基于计数的方法
使用基于同义词词典的方法,需要人工逐个定义单词之间的相关性。这 样的工作非常费力,在表现力上也存在限制(比如,不能表示细微的差别)。
而基于计数的方法从语料库中自动提取单词含义,并将其表示为向量。具体 来说,首先创建单词的共现矩阵,将其转化为 PPMI 矩阵,再基于 SVD 降 维以提高稳健性,最后获得每个单词的分布式表示。另外,我们已经确认 过,这样的分布式表示具有在含义或语法上相似的单词在向量空间上位置相 近的性质。
为了方便处理语料库的文本数据,我们实现了几个预处理函数。具体来说,包括测量向量间相似度的函数(cos_similarity())、用于显示相似单词 的排名的函数(most_similar())。这些函数在后面的章节中还会用到。
本章所学的内容
- 使用 WordNet 等同义词词典,可以获取近义词或测量单词间的相似度等
- 使用同义词词典的方法存在创建词库需要大量人力、新词难更新等问题
- 目前,使用语料库对单词进行向量化是主流方法
- 近年来的单词向量化方法大多基于“单词含义由其周围的单词构成” 这一分布式假设
- 在基于计数的方法中,对语料库中的每个单词周围的单词的出现频 数进行计数并汇总(= 共现矩阵)
- 通过将共现矩阵转化为 PPMI 矩阵并降维,可以将大的稀疏向量转变为小的密集向量
- 在单词的向量空间中,含义上接近的单词距离上理应也更近