UVa 11817 - Tunnelling the Earth

题目：给出地球上的两个点的经度和纬度，计算两点球面距离和两点的空间距离差。

分析：计算几何、大地坐标系。利用公式可直接解得两点的空间距离：

            d = r*sqrt(2-2*(cos(lat1)*cos(lat2)*cos(lon1-lon2)+sin(lat1)*sin(lat2)))

            推导过程如下：

                      

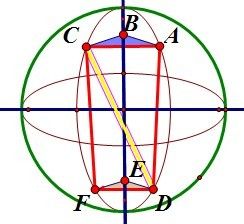
            如图，C，D为已知两点则有如下推导：            

            AB = r*cos(lat1)；DE = r*cos(lat2)；BE = r*sin(lat1) + r*sin(lat2)；

            AD*AD = BE*BE + (AB-DE)*(AB-DE) = 2*r*r - 2*r*r*sin(lat1)*sin(lat2) - 2*r*r*cos(lat1)*cos(lat2)；

            AC*AC = 2*AB*AB - 2*AB*AB*cos(lon1-lon2) = 2*r*r*cos(lat1)*cos(lat1)*(1-cos(lon1-lon2))；

            DF*DF = 2*DE*DE - 2*DE*DE*cos(lon1-lon2) = 2*r*r*cos(lat2)*cos(lat2)*(1-cos(lon1-lon2))；

            AC*DF = 2*r*r*cos(lat1)*cos(lat2)*(1-cos(lon1-lon2))；

            由托勒密定理有 AC*DF + AD*AD = CD*CD 整理有：

            CD = r*sqrt(2-2*(cos(lat1)*cos(lat2)*cos(lon1-lon2)+sin(lat1)*sin(lat2)))；

注意：输出最近的整数，%.0lf即可。

 

#include <stdio.h>

#include <stdlib.h>

#include <math.h>



int main()

{

	double r = 6371009;

	double p = acos(-1.0);

	

	int    n;

	double l1,d1,l2,d2;

	while ( scanf("%d",&n) != EOF )

	while ( n -- ) {

		scanf("%lf%lf%lf%lf",&l1,&d1,&l2,&d2);

		l1 *= p/180.0; l2 *= p/180.0;

		d1 *= p/180.0; d2 *= p/180.0;

		

		double d = r*sqrt(2-2*(cos(l1)*cos(l2)*cos(d1-d2)+sin(l1)*sin(l2)));

		printf("%.0lf\n",2*asin(d/(2*r))*r-d);

	}

	return 0;

}