算法入门——树(基础篇)(tree)
数据结构--树
- 1.二叉树的表达方式
- 2.由括号表示法构建二叉树
- 3.遍历二叉树
-
- (1)层次遍历:
- (2)括号表示法输出
-
- 1.递归
- 2.非递归
- (3)前序遍历
- (4)中序遍历
- (5)后序遍历
1.二叉树的表达方式
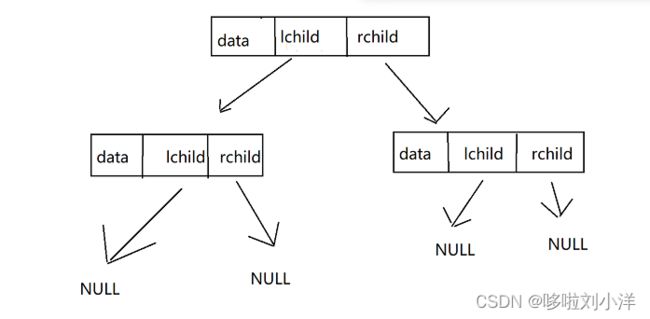
定义一个结构体来存储二叉树的节点
typedef char ElemType; //定义char为数据类型
typedef struct node //节点类型
{
ElemType data; //存放的数据
struct node *lchild; //指向它的左孩子
struct node *rchild; //指向它的右孩子
}BTnode //BTnode是''struct node ''的别名
2.由括号表示法构建二叉树
现在有一颗二叉树,如下图:
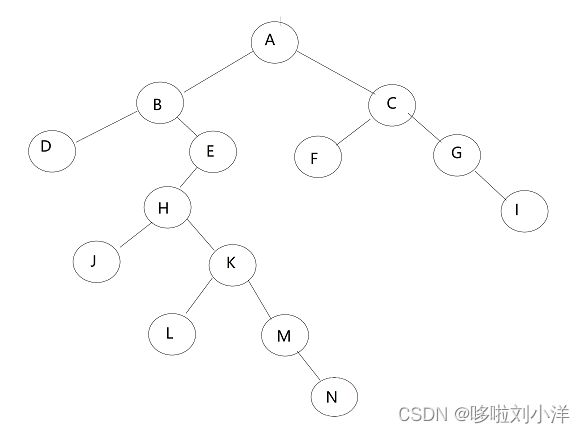
如果用括号表示法来描述上面这颗二叉树,可以这样做:
A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))
总结一下规律:
- 当字母后面遇到‘( ’:说明当前字母表示的节点有孩子节点
- ‘,’表示有右孩子节点
- ‘(’总是和离自己最近的‘)’匹配,表示某个根节点的所有子孙节点的集合(例如 A(B,(C,D),F) 这里BCDF都是根节点A的子节点)
上面三条规律是非常容易找到的,那么如何右它去创建一个二叉树呢?
栈!
由于始终希望越是上层的根节点处理的越晚,所以应该将最开始的根节点压入栈
根据栈先进后出,后进先出的严格规律,后处理的先放入,先处理的后放入。
遍历括号表示法
- 当遇到字母,创建新节点存储字母值,当前节点有两种可能,要么是最开始的根节点,要么就一定是某个节点的孩子节点。那么应该让之前已经压入栈的栈顶元素(也就是包含该孩子节点的父节点)指向这个孩子节点
- 遇到‘(’,说明之前创建的节点有孩子节点,将刚刚创建的节点入栈,成为新的栈顶元素
- 遇到‘)’,匹配离当前最近的‘(’,而栈顶元素是遇到‘(’就入栈,成为最新的栈顶元素,所以栈顶元素应该是这一对‘(,)’的根节点。所以应该将栈顶元素退栈
- 遇到‘,’:说明将要处理当前根节点的右孩子节点。
总结
从根节点开始,每当当前节点有孩子节点,那么将当前节点入栈。
从栈顶开始,每当栈顶元素的孩子节点处理完,那么将栈顶元素出栈。
代码有点难度:
void CreatBTNode(BTNode *&root,string &str)
{
//先准备处理工具
BTNode *St[110]; //指针数组,St[i]表示下标为i的元素存储的值是一个指针,
//该指针的类型是BTNode *
int top=-1; //St数组用来模拟栈,那么这是栈指针
int k=0; //判断处理左右孩子节点
int len=str.length(); //遍历长度
int j=0;
char ch=str[j];
while(len) //遍历str字符串
{
switch(ch)
{
case '(': top++;St[top]=p;k=1;break;
case ')': top--;break;
case ',': k=2;break;
default:
p=(BTNode*)malloc(sizeof(BTNode));
p->data=ch;
p->lchild=p->rchild=NULL;
if(root=NULL)
root=p;
else
{
switch(k)
{
case 1:St[top]->lchild=p;break;
case 2:St[top]->rchild=p;break;
}
}
}
len--;
j++;
ch=str[j];
}
}
3.遍历二叉树
如何验证上面的代码呢?
有四种方式:
- 层次遍历
- 括号表示法输出
- 前序遍历
- 中序遍历
- 后序遍历
(1)层次遍历:
层次遍历:一层一层遍历,规定每一次的遍历顺序是从左到右。
上面的二叉树的层次遍历是:
ABCDEFGHIJKLMN
层次遍历的规律是先进先出,后进后出。很显然,是队列的特性。所以模拟队列来进行层次遍历
void arrageTraversal(BTNode *root) //层次遍历
{
BTNode* qu[N]; //指针数组
int front = 0, rear = 1; //front是队头,出队的地方。rear是队尾,入队的地方,rear指向队尾元素的前一位
qu[front] = root;
while (front!=rear) //栈不空
{
BTNode* p = qu[front]; //出队
front++; //队头后移一个单位,也就是队头成为之前的第二个元素,想象队头在左边,队尾在右边。加一个元素,队尾往后面移动一个单位,出队一个元素,队头往左边移动一个单位
cout << p->data << " ";
if (p->lchild != NULL)
{
qu[rear] = p->lchild;
rear++;
}
if (p->rchild != NULL)
{
qu[rear] = p->rchild;
rear++;
}
}
}
(2)括号表示法输出
首先找到括号的规律,再写代码
- 遇到字符,输出
- 如果该字符有孩子节点,输出’(’
- 如果退栈节点是左孩子,输出‘,’
- 如果退栈节点是右孩子,输出‘)’
1.递归
void dfs_KH(BTNode* root) //递归写法
{
if (root == NULL)
return;
cout << root->data;
if (root->lchild != NULL || root->rchild != NULL)
{
cout << '(';
dfs_KH(root->lchild); //这一步实际上是退栈左孩子
if(root->rchild!=NULL)
cout << ',';
dfs_KH(root->rchild); //这一步实际上是退栈右孩子
cout << ')';
}
}
2.非递归
//暂时还没有想出来,,,
//也许想出来了!
//还是不行。。
//这次真写出来了。花了5个小时左右...
//给个建议,没有想明白的时候不要乱写,即扰乱思路又浪费时间
/*
将栈顶元素出栈,如果栈顶元素之前没有出现过,输出它,否则栈顶元素是退栈元素(也是当前根节点),要么输出‘)’,要么输出'),'。
如果栈顶元素有孩子节点,孩子节点入栈并且标记是左孩子还是右孩子。且将当前栈顶元素的左右孩子置空
如果栈顶元素的左孩子为空,输出',',如果栈顶元素的右孩子为空,将左孩子标记为右孩子
如果栈顶元素没有孩子节点且之前没有输出过(当前while循环不算第一次),如果该节点是左孩子,输出‘,’,否则啥也不做。
如果栈顶元素没有孩子节点且之前输出过,则如果它是左孩子,输出'),'否则输出')'
*/
typedef struct stack
{
int k; //k==1表示是左孩子,k==2表示是右孩子
int j; //j==0表示没输出过,j==1表示输出过,
BTNode* p;
stack():k(0),p(NULL),j(0) {}
}stack;
void expression_KH(BTNode *root)// 括号表示法,非递归
{
//括号表示法用递归感觉很简单,不用递归有点难,尝试一下
stack st[N]; //模拟栈
int top = 0;
st[top].k = 2; //表示根节点是右孩子
st[top].p = root;
while (top!=-1)//A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))
{
BTNode* temp = st[top].p; //取栈顶
if(st[top].j==0)
cout << temp->data;
if ((temp->lchild != NULL || temp->rchild != NULL)) //如果当前节点有孩子节点
{
cout << '(';
st[top].j = 1;
if (temp->rchild != NULL)
{
top++;
st[top].k = 2;
st[top].p = temp->rchild;
st[top].j = 0;
}
if (temp->lchild != NULL)
{
top++;
if (temp->rchild == NULL)
st[top].k = 2;
else
st[top].k = 1;
st[top].p = temp->lchild;
st[top].j = 0;
}
else if(temp->lchild==NULL)
cout << ',';
temp->lchild = temp->rchild= NULL;
}
else
{
if (st[top].j == 1)
{
if (st[top].k == 1)
cout << "),";
else
cout << ')';
top--;
}
else
{
if (st[top].k == 1)
cout << ',';
top--;
}
}
}
}
(3)前序遍历
ABDEHJKLMNCFGI
struct Node
{
BTNode* r;
int k,L;
Node():k(0),r(NULL){}
Node(BTNode *a):r(a),k(0),L(0) {}
Node(BTNode *a,int b):r(a),k(b),L(0) {}
};
void preorder(BTNode* root) //非递归
{
//(1)先输出根节点(2)如果有孩子节点,先放入右孩子,再放入左孩子
stack<Node>st;
st.push({ root});
while (!st.empty())
{
Node temp = st.top();
st.pop();
cout << temp.r->data;
if (temp.r->rchild != NULL)
st.push({ temp.r->rchild});
if (temp.r->lchild != NULL)
st.push({ temp.r->lchild});
}
}
(4)中序遍历
左孩子->根节点->右孩子
DBJHLKMNEAFCGI
DBJHLKMNEAFCGI
void inorder(BTNode* root)
{
stack<Node>st;
st.push({ root });
while (!st.empty())
{
Node temp = st.top();
if (temp.r->lchild != NULL&&temp.k==0)
{
st.top().k = 1;
st.push({ temp.r->lchild });
continue;
}
cout << temp.r->data; //没有左孩子,输出当前节点
st.pop();
if (temp.r->rchild != NULL) //再看右孩子
{
st.push({ temp.r->rchild });
}
}
}
(5)后序遍历
左孩子->右孩子->根节点
DJLNMKHEBFIGCA
DJLNMKHEBFIGCA
void postorder(BTNode* root)
{
stack<Node>st;
st.push({ root });
while (!st.empty())
{
Node temp = st.top();
if (temp.k == 0 && temp.r->lchild != NULL)
{
st.top().k = 1;
st.push({ temp.r->lchild });
continue;
}
if (temp.L==0&&temp.r->rchild != NULL)
{
st.top().L = 1;
st.push({ temp.r->rchild });
continue;
}
cout << temp.r->data;
st.pop();
}
}