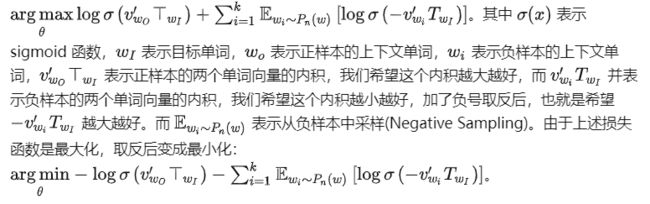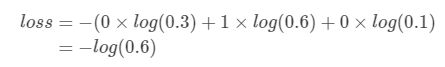一篇文章入门Word2Vec

NLP

一、Word Embedding

1、Word Embedding的基本概念

现有的机器学习方法往往无法直接处理文本数据，因此需要找到合适的方法，将文本数据转换为数值型数据，由此引出了Word Embedding的概念。如果将word看作文本的最小单元，可以将Word Embedding理解为一种映射，其过程是：将文本空间中的某个word，通过一定的方法，映射或者说**嵌入（embedding）**到另一个数值向量空间

Word Embedding的输入是原始文本中的一组不重叠的词汇，假设有句子：apple on a apple tree。那么为了便于处理，我们可以将这些词汇放置到一个dictionary里，例如：[“apple”, “on”, “a”, “tree”]，这个dictionary就可以看作是Word Embedding的一个输入。

Word Embedding的输出就是每个word的向量表示。对于上文中的原始输入，假设使用最简单的one hot编码方式，那么每个word都对应了一种数值表示。例如，apple对应的vector就是**[1, 0, 0, 0]，a对应的vector就是[0, 0, 1, 0]**

2、Word Embedding的类型

• 基于频率的Word Embedding（Frequency based embedding）
• 基于预测的Word Embedding（Prediction based embedding）

基于频率的Word Embedding

基于频率的Word Embedding又可细分为如下几种：

• Count Vector
• TF-IDF Vector
• Co-Occurence Vector

其本质都是基于one-hot表示法的，以频率为主旨的加权方法改进

Count Vector

假设有一个语料库C，其中有D个文档：{d1, d2, …, dD}，C中一共有N个word。这N个word构成了原始输入的dictionary，我们据此可以生成一个矩阵M，其规模是D X N。

假设语料库内容如下：
D1: He is a boy.
D2: She is a girl, good girl.

那么可以构建如下2 × 7维的矩阵：

该矩阵便是一个counter vector matrix。每个文档用词向量的组合来表示，每个词的权重用其出现的次数来表示。

当然，如果语料库十分庞大，那么dictionary的规模亦会十分庞大，因此上述矩阵必然是稀疏的，会给后续运算带来很大的麻烦。通常的做法是选取出现次数最频繁的那些词来构建dictionary（例如，top 10,000个词），这样会有效缩减上述矩阵的规模。

TF-IDF

在Count Vector中，构建词的权重时只考虑了词频TF（Term Frequency），也就是词在单个文档中出现的频率。直觉上来看，TF越大，说明词在本文档中的重要性越高，对应的权重也就越高。这个思路大体上来说是对的，例如，对于一个主题是Cat的文档，显然Cat这个词汇在本文档中的出现频率会相对高。

但如果我们把视野扩展到整个语料库，会发现，像is，a等通用词汇，几乎在每个文档里出现的频率都很高。由此，我们可以得到这样的结论：对于一个word，如果在特定文档里出现的频率高，而在整个语料库里出现的频率低，那么这个word对于该文档的重要性就比较高。因此我们可以引入逆文档频率IDF（Inverse Document Frequency）的概念：IDF=log(N/n)。其中，N代表语料库中文档的总数，n代表某个word在几个文档中出现过；当一个word出现地越频繁，那么IDF就越小。显然，IDF用于惩罚那些常用词汇，而TF用于奖励那些在特定文档中出现频繁的词汇。二者的乘积TF X IDF用来表示词汇的权重，显然合理性大大增强。

举例：
语料库中共有2个文档，其中有一个文档名为d。

• 共有1个文档出现了cat这个词汇；且在特定文档d中，共有8个词汇，cat出现了4次。
• 共有2个文档出现了is这个词汇；且在特定文档d中，共有8个词汇，is出现了4次。

那么根据定义，可以得到：

TF("cat", d)=4/8=0.5
TF("is", d)=4/8=0.5
IDF("cat", d) = log(2/1)=0.301
IDF("is", d) = log(2/2)=0
TFIDF("cat", d)=TF("cat", d)*IDF("cat", d)=0.5*0.301=0.15
TFIDF("is", d)=TF("is", d)*IDF("is", d)=0.5*0=0

TFIDF算法极大地惩罚了is这个词汇，从而增加了权重设置的合理性。

Co-Occurence Vector

自然语言一大特色是语义和上下文，相似的单词趋向于有相似的上下文(context)

举例：

• 那个人是个男孩。
• 那个人是个女孩。

男孩和女孩从概念上来说相似，他们也具有相似的上下文

根据如上思想，我们可以构建一套算法，来实现基于上下文的特征构建

这里需要引入两个概念：

1. Context Window：上面我们提到了context，但context的长度需要有一个界定，也就是说，对于一个给定的word，需要有一个Context Window大小的概念。

如果指定Context Window大小为2，范围为前后两个word，那么对于such这个词，它的Context Window如上图所示

2. Co-Occurence（共现）：对于such这个单词来说，在其上下文窗口内，它分别与**[she, is, a, beautiful]这四个单词各出现了一次共现。如果我们在语料库中所有such出现的地方，计算其共现的单词，并按次数累加，那么我们就可以利用其上下文范围内的单词来表示such这个词，这就是Co-Occurence Vector**的计算方法。.

   假设有如下语料库：
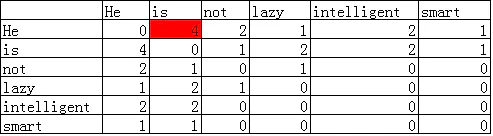
   He is not lazy. He is intelligent. He is smart.
   如果Context Window大小为2，那么可以得到如下的共现矩阵：

   

   我们可以看看He和is的共现次数4是如何计算出来的：

   

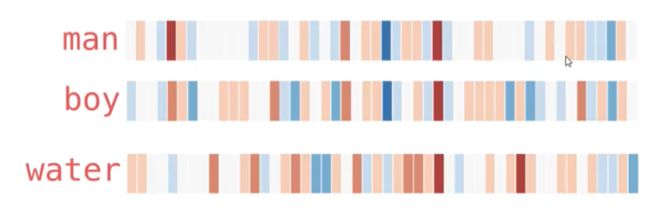
共现矩阵最大的优势是这种表示方法保留了语义信息，例如，通过这种表示，就可以知道，man和woman是更加接近的，而man和apple是相对远的。相比前述的两种方法，更具有智能的味道。

二、Word2Vec

1、one-hot representation

表示简单

问题：词越多，维数越高（词表大小V），无法表示词和词之间的关系

通常，数据的维度越高，能提供的信息也就越多，从而计算结果的可靠性就更值得信赖

2、余弦相似度

两个向量间的余弦值可以通过使用欧几里得点积公式求出：

余弦函数在三角形中的计算公式为：

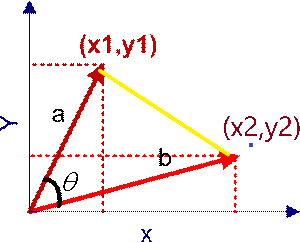
在直角坐标系中，向量表示的三角形的余弦函数是怎么样的呢？下图中向量a用坐标(x1,y1)表示，向量b用坐标(x2,y2)表示。

向量a和向量b在直角坐标中的长度为：
向量a和向量b之间的距离我们用向量c表示，就是上图中的黄色直线，那么向量c在直角坐标系中的长度为
将a，b，c带入三角函数的公式中得到如下的公式：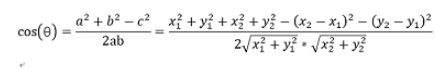

这是2维空间中余弦函数的公式，那么多维空间余弦函数的公式就是：给定两个属性向量， A 和B，其余弦相似性θ由点积和向量长度给出，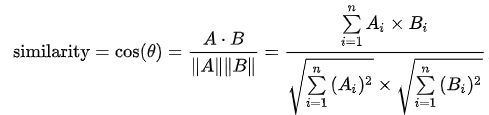

这里的A_i和B_i分别代表向量A和向量B的各分量

余弦相似度越小，距离越大。相似度越大，距离越小。

假设有3个物品，item1，item2和item3，用向量表示分别为：
$$item1[1,1,0,0,1]$$

$$item2[0,0,1,2,1]$$

$$item3[0,0,1,2,0]$$

即五维空间中的3个点。用欧式距离公式计算item1、itme2之间的距离，以及item2和item3之间的距离，分别是：
$$item1-item2=(1-0{)}^2+(1-0{)}^2+(0-1{)}^2+(0-2{)}^2+(1-1{)}^2=7$$

$$item2-item3=(0-0{)}^2+(0-0{)}^2++(1-1{)}^2+(2-2{)}^2+(1-0{)}^2=1$$

用余弦函数计算item1和item2夹角间的余弦值为：
$$\cos (\theta )=\frac{1}{3\sqrt{2}}$$
用余弦函数计算item2和item3夹角间的余弦值为：
$$\cos (\theta )=\frac{5}{\sqrt{30}}$$
由此可得出item1和item2相似度小，两个之间的距离大(距离为7)，item2和itme3相似度大，两者之间的距离小(距离为1)。

余弦相似度算法：一个向量空间中两个向量夹角间的余弦值作为衡量两个个体之间差异的大小，余弦值接近1，夹角趋于0，表明两个向量越相似，余弦值接近于0，夹角趋于90度，表明两个向量越不相似。

---

下面我们介绍使用余弦相似度计算两段文本的相似度

• 句子A：这只皮靴号码大了。那只号码合适。
• 句子B：这只皮靴号码不小，那只更合适。

使用结巴分词对上面两个句子分词后，分别得到两个列表：

• listA=[‘这‘, ‘只‘, ‘皮靴‘, ‘号码‘, ‘大‘, ‘了‘, ‘那‘, ‘只‘, ‘号码‘, ‘合适‘]
• listB=[‘这‘, ‘只‘, ‘皮靴‘, ‘号码‘, ‘不小‘, ‘那‘, ‘只‘, ‘更合‘, ‘合适‘]

将listA和listB放在一个set中，得到：set={‘不小’, ‘了’, ‘合适’, ‘那’, ‘只’, ‘皮靴’, ‘更合’, ‘号码’, ‘这’, ‘大’}

将上述set转换为dict，key为set中的词，value为set中词出现的位置

dict1={‘不小’: 0, ‘了’: 1, ‘合适’: 2, ‘那’: 3, ‘只’: 4, ‘皮靴’: 5, ‘更合’: 6, ‘号码’: 7, ‘这’: 8, ‘大’: 9}

将每个字转换为出现在set中的位置，转换后为：

• listAcode=[8, 4, 5, 7, 9, 1, 3, 4, 7, 2]
• listBcode=[8, 4, 5, 7, 0, 3, 4, 6, 2]

对listAcode和listBcode进行oneHot编码，oneHot编号后得到的结果如下：

• listAcodeOneHot = [0, 1, 1, 1, 2, 1, 0, 2, 1, 1]
• listBcodeOneHot = [1, 0, 1, 1, 2, 1, 1, 1, 1, 0]

计算两个向量listAcodeOneHot和listBcodeOneHot的余弦相似度：
$$\cos (\theta )=\frac{10}{\sqrt{14}\ast \sqrt{11}}=0.81$$
根据余弦相似度，句子A和句子B相似度很高。

import jieba
import math

s1 = '这只皮靴号码大了那只号码合适'

'''
jieba.cut():
    The main function that segments an entire sentence that contains Chinese characters into separated words.
'''
s1_cut = [i for i in jieba.cut(s1, cut_all=True) if i != '']
s2 = '这只皮靴号码不小那只更合适'
s2_cut = [i for i in jieba.cut(s2, cut_all=True) if i != '']

print(s1_cut)
print(s2_cut)
word_set = set(s1_cut).union(set(s2_cut))
print(word_set)

word_dict = dict()
i = 0
for word in word_set:
    word_dict[word] = i
    i += 1
print(word_dict)

s1_cut_code = [word_dict[word] for word in s1_cut]
print(s1_cut_code)

s1_cut_code = [0] * len(word_dict)
print(s1_cut_code)

for word in s1_cut:
    s1_cut_code[word_dict[word]] += 1
print(s1_cut_code)

s2_cut_code = [word_dict[word] for word in s2_cut]
print(s2_cut_code)

s2_cut_code = [0] * len(word_dict)
print(s2_cut_code)
for word in s2_cut:
    s2_cut_code[word_dict[word]] += 1
print(s2_cut_code)

# 计算余弦相似度
sum = 0
sq1 = 0
sq2 = 0
for i in range(len(s1_cut_code)):
    sum += s1_cut_code[i] * s2_cut_code[i]
    sq1 += pow(s1_cut_code[i], 2)
    sq2 += pow(s2_cut_code[i], 2)

try:
    # round(): Round a number to a given precision in decimal digits.
    result = round(float(sum) / (math.sqrt(sq1) * math.sqrt(sq2)), 2)
except ZeroDivisionError:
    result = 0.0
print(f"余弦相似度：{result}")

3、浅析Word2Vec

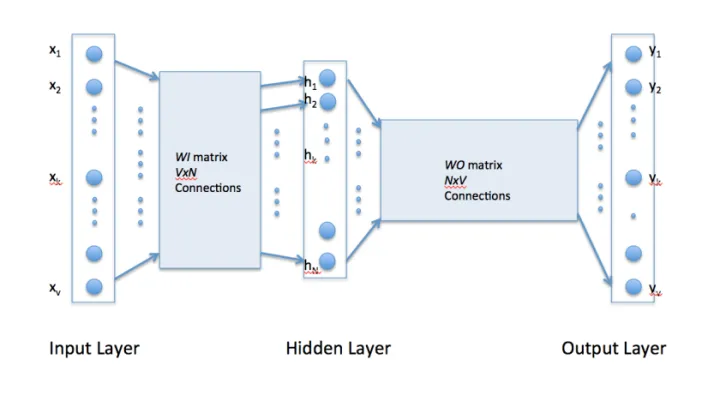
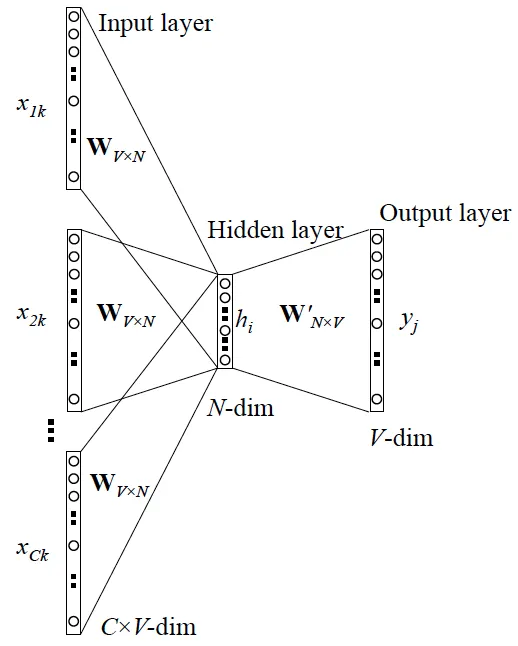
使用Word2Vec可以将词语转换成向量，Word2vec使用单个隐藏层，完全连接的神经网络如下所示：

例如，具有以下句子的训练语料库：“The dog saw a cat”，“Dog chasing cat”，“Cat climbed a tree”

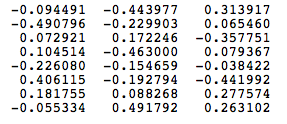
语料库词汇有八个单词[‘a’,‘cat’,‘chasing’,‘climbed’,‘dog’,‘saw’,‘the’,‘tree’]。按字母顺序排序后，每个单词都可以通过其索引引用。对于这个例子，我们的神经网络将有八个输入神经元和八个输出神经元。让我们假设我们决定在隐藏层中使用三个神经元。这意味着WI和WO将分别是8×3和3×8矩阵。在训练开始之前，这些矩阵被初始化为随机值，假设WI和WO初始化为以下值：

WI =

WO=

假设我们希望网络学习单词“cat”和“climbed”之间的关系，单词“cat”被称为context word，单词“climbed”被称为target word。在这种情况下，输入矢量X将是[0 1 0 0 0 0 0 0]，目标矢量是[0 0 0 1 0 0 0 0]。

利用表示“cat”的输入向量，可以将隐藏层神经元的输出计算为：
$$H=X\ast WI=[-0.490796-0.2299030.065460]$$
实际上隐藏层神经元输出的向量H复制了WI矩阵的第二行的权重，输出层神经元的输入计算为：
$$H_{=}H\ast WO=[0.100934-0.309331-0.122361-0.1513990.143463-0.051262-0.0796860.112928]$$
采用softmax作为激活函数，将输出向量中的数值转换为概率：

[0.143073 0.094925 0.114441 0.111166 0.149289 0.122874 0.119431 0.144800]

粗体的概率是针对所选择的目标词“climbed”,很显然它不是最大的，所以我们需要改进它，采用交叉熵和BP算法反向改进权重

词向量（50维）：

由上图可以发现，相似的词在特征表达中比较相似

不同模型对比

CBOW

CBOW的全称是continuous bag of words（连续词袋模型）。其本质也是通过context word（背景词）来预测target word（目标词）。

上述target word“climbed”的context word只有一个“cat”作为训练样本，而在CBOW中，可由多个context word表示。

例如，我们可以使用“cat”和“tree”作为“climbed”的context word。这需要修改神经网络架构。如下所示，修改包括将输入层复制C次（C的大小就是window的大小），以及在隐藏层神经元中添加除以C的操作。

**CBOW是依据背景词来预测目标词。**具体算法如下：

1. 第一步是计算隐藏层h的输出：
   $$h=\frac{1}{C}WI\ast (\sum _{i=1}^C{x}_i)$$

2. 第二步是计算在输出层每个结点的输入：
   $$u_j=h\ast W{O}_j$$

3. 接着我们计算输出层的输出，也就是将Softmax用作激活函数

4. 最后使用交叉熵作为loss function，用BP算法更新权重

Skip-Gram

和CBOW用背景词预测目标词不同的是，Skip-Gram是利用目标词预测背景词

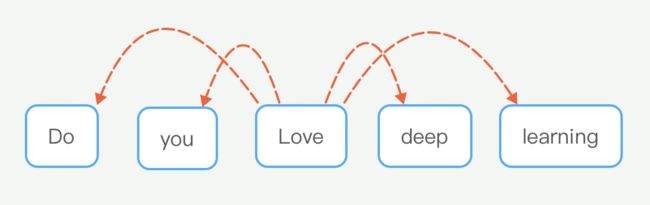
Skip-gram算法就是在给出目标单词（中心单词）的情况下，预测它的上下文单词（除中心单词外窗口内的其他单词，这里的窗口大小是2，也就是左右各两个单词）。

图中的love是目标单词，其他是上下文单词，那么我们就是求：
$$P(w_{you}|w_{love})、P(w_{Do}|w_{love})、P(w_{deep}|w_{love})、P(w_{learning}|w_{love})$$
我们的目标是计算在给定单词的条件下，其他单词出现的概率

Skip-gram是一个具有3层结构的神经网络，分别是：

Input Layer（输入层）：接收一个one-hot张量V，里面存储着当前句子中心词的one-hot表示

Hidden Layer（隐藏层）：将张量V乘以一个word embedding张量W₁，并把结果作为隐藏层的输出，里面存储着当前句子中心词的词向量。

Output Layer（输出层）：将隐藏层的结果乘以另一个word embedding张量W₂，并将结果经过softmax变换后，就得到了使用当前中心词与上下文的预测结果

在实际操作中，使用一个滑动窗口（一般情况下，长度是奇数），从左到右开始扫描当前句子。每个扫描出来的片段被当成一个小句子，每个小句子中间的词被认为是中心词，其余的词被认为是这个中心词的上下文。

4、深入Word2Vec

什么是Word2Vec？

NLP（自然语言处理）中最细粒度的是词语，词语组成句子，句子再组成段落、篇章、文档

举个简单例子，判断一个词的词性，是动词还是名词。用机器学习的思路，我们有一系列样本(x,y)，这里 x 是词语，y 是它们的词性，我们要构建 f(x)->y 的映射，但这里的数学模型 f（比如神经网络、SVM）只接受数值型输入，而 NLP 里的词语，是人类的抽象总结，是符号形式的（比如中文、英文、拉丁文等等），所以需要把他们转换成数值形式，或者说——嵌入到一个数学空间里，这种嵌入方式，就叫词嵌入（word embedding)，而 Word2vec，就是词嵌入（ word embedding) 的一种

有监督机器学习模型：f(x)->y

在 NLP 中，把 x 看做一个句子里的一个词语，y 是这个词语的上下文词语，那么这里的 f，便是 NLP 中经常出现的『语言模型』（language model）：词语x和词语y放在一起，是不是人话。

Word2vec 正是来源于这个思想，但它的最终目的，不是要把 f 训练得多么完美，而是只关心模型训练完后的副产物——模型参数（这里特指神经网络的权重），并将这些参数，作为输入 x 的某种向量化的表示，这个向量便叫做——词向量

我们来看个例子，如何用 Word2vec 寻找相似词：

• 对于一句话：『她们 夸 吴彦祖 帅 到 没朋友』，如果输入 x 是『吴彦祖』，那么 y 可以是『她们』、『夸』、『帅』、『没朋友』这些词
• 现有另一句话：『她们 夸 我 帅 到 没朋友』，如果输入 x 是『我』，那么不难发现，这里的上下文 y 跟上面一句话一样
• 从而 f(吴彦祖) = f(我) = y，所以大数据告诉我们：我 = 吴彦祖（完美的结论）

Skip-gram 和 CBOW 模型

语言模型：

• 如果是用一个词语作为输入，来预测它周围的上下文，那这个模型叫做『Skip-gram 模型』
• 而如果是拿一个词语的上下文作为输入，来预测这个词语本身，则是 『CBOW 模型』

Skip-gram 和 CBOW 的简单情形

上面说到，y 是 x 的上下文，所以 y 只取上下文里一个词语的时候，语言模型就变成：

用当前词 x 预测它的下一个词 y

一般的数学模型只接受数值型输入，这里的 x 该怎么表示呢？ 显然不能用 Word2vec，因为这是我们训练完模型的产物，现在我们想要的是 x 的一个原始输入形式。

答案是：one-hot encoder

假设全世界所有的词语总共有 V 个，这 V 个词语有自己的先后顺序，假设『吴彦祖』这个词是第1个词，『我』这个单词是第2个词，那么『吴彦祖』就可以表示为一个 V 维全零向量、把第1个位置的0变成1，而『我』同样表示为 V 维全零向量、把第2个位置的0变成1。这样，每个词语都可以找到属于自己的唯一表示。

那我们接下来就可以看看 Skip-gram 的网络结构了，x 就是上面提到的 one-hot encoder 形式的输入，y 是在这 V 个词上输出的概率，我们希望跟真实的 y 的 one-hot encoder 一样。

首先说明一点：隐层的激活函数其实是线性的，相当于没做任何处理（这也是 Word2vec 简化之前语言模型的独到之处），我们要训练这个神经网络，用反向传播算法，本质上是链式求导

---

当模型训练完后，最后得到的其实是神经网络的权重，比如现在输入一个 x 的 one-hot encoder: [1,0,0,…,0]，对应刚说的那个词语『吴彦祖』，则在输入层到隐含层的权重里，只有对应 1 这个位置的权重被激活，这些权重的个数，跟隐含层节点数是一致的，从而这些权重组成一个向量 vx 来表示x，而因为每个词语的 one-hot encoder 里面 1 的位置是不同的，所以，这个向量 vx 就可以用来唯一表示 x。

注意：上面这段话说的就是 Word2vec 的精髓！！

---

此外，我们刚说了，输出 y 也是用 V 个节点表示的，对应V个词语，所以其实，我们把输出节点置成 [1,0,0,…,0]，它也能表示『吴彦祖』这个单词，但是激活的是隐含层到输出层的权重，这些权重的个数，跟隐含层一样，也可以组成一个向量 vy，跟上面提到的 vx 维度一样，并且可以看做是词语『吴彦祖』的另一种词向量。而这两种词向量 vx 和 vy，正是 Mikolov 在论文里所提到的，『输入向量』和『输出向量』，一般我们用『输入向量』。

需要提到一点的是，这个词向量的维度（与隐含层节点数一致）一般情况下要远远小于词语总数 V 的大小，所以 Word2vec 本质上是一种降维操作——把词语从 one-hot encoder 形式的表示降维到 Word2vec 形式的表示。

Skip-gram 更一般的情形

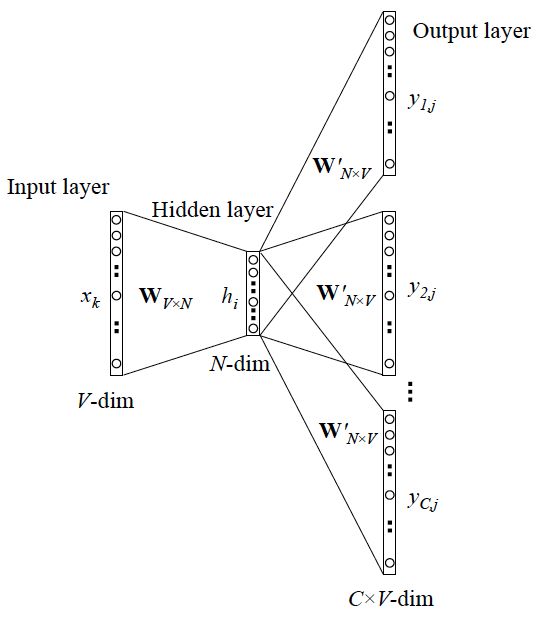
上面讨论的是最简单情形，即 y 只有一个词，当 y 有多个词时，网络结构如下：

CBOW 更一般的情形

Skip-gram 是预测一个词的上下文，而 CBOW 是用上下文预测这个词

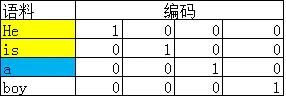
如上图所示，首先语料库内的每个word都可以用one-hot的方式编码。假设选取Context Window为2，那么模型中的一对input和target就是：

• input：He和is的one-hot编码
• target：a的one-hot编码

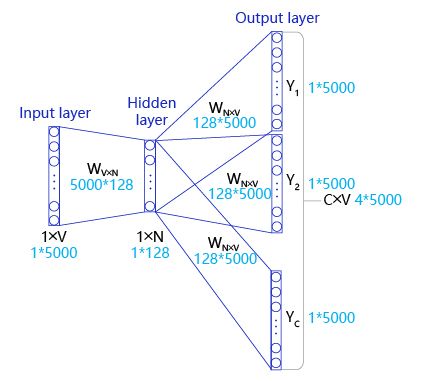
接着通过一个浅层神经网络来拟合该结果，如下图所示：

过程简单介绍如下：

1. 输入为C个V维的vector。其中C为上下文窗口的大小，V为原始编码空间的规模。例如，示例中的C=2，V=4.两个vector分别为4维的He和is的one-hot编码形式；
2. 在输入层和隐藏层之间，每个input vector分别乘以一个VxN维度的矩阵，得到后的向量各个维度做平均，得到隐藏层的权重。隐藏层乘以一个NxV维度的矩阵，得到output layer的权重；
3. 隐藏层的维度设置为理想中压缩后的词向量维度。示例中假设我们想把原始的4维的原始one-hot编码维度压缩到2维，那么N=2；
4. 输出层是一个softmax层，用于组合输出概率。所谓的损失函数，就是这个output和target之间的的差（output的V维向量和input vector的one-hot编码向量的差），该神经网络的目的就是最小化这个loss；

输入为多个单词，需要对输入进行处理（一般是求和然后平均）

5、实现Skip-gram

Skip-gram的理想实现

在理想情况下，我们可以使用一个简单的方式实现skip-gram。即把需要推理的每个目标词都当成一个标签，把skip-gram当成一个大规模分类任务进行网络构建，过程如下：

1. 声明一个形状为[vocab_size, embedding_size]的张量，作为需要学习的词向量，记为W0。对于给定的输入V，使用向量乘法，将V乘以W0，这样就得到了一个形状为[batch_size, embedding_size]的张量，记为H=V×W0。这个张量H就可以看成是经过词向量查表后的结果。
2. 声明另外一个需要学习的参数W1，这个参数的形状为[embedding_size, vocab_size]。将上一步得到的H去乘以W1，得到一个新的tensor O=H×W1，此时的O是一个形状为[batch_size, vocab_size]的tensor，表示当前这个mini-batch中的每个中心词预测出的目标词的概率。
3. 使用softmax函数对mini-batch中每个中心词的预测结果做归一化，即可完成网络构建。

Skip-gram的实际实现

然而在实际情况中，vocab_size通常很大（几十万甚至几百万），导致W0和W1也会非常大。为了缓解这个问题，通常采取负采样（negative sampling）的方式来近似模拟多分类任务。

随机从词表中选择几个代表词，通过最小化这几个代表词的概率，去近似最小化整体的预测概率。比如，先指定一个中心词（如“人工”）和一个目标词正样本（如“智能”），再随机在词表中采样几个目标词负样本（如“日本”，“喝茶”等）。有了这些内容，我们的skip-gram模型就变成了一个二分类任务。对于目标词正样本，我们需要最大化它的预测概率；对于目标词负样本，我们需要最小化它的预测概率。通过这种方式，我们就可以完成计算加速。上述做法，我们称之为负采样。

如果 vocabulary 大小为10000时， 当输入样本 ( “fox”, “quick”) 到神经网络时， “ fox” 经过 one-hot 编码，在输出层我们期望对应 “quick” 单词的那个神经元结点输出 1，其余 9999 个都应该输出 0。在这里，这9999个我们期望输出为0的神经元结点所对应的单词我们为 negative word. negative sampling 的想法也很直接 ，将随机选择一小部分的 negative words，比如选 10个 negative words 来更新对应的权重参数。

negative sample也是根据他们出现概率来选的，而这个概率又和他们出现的频率有关。更常出现的词，更容易被选为negative sample。

选用更常出现的词作为negative sample的原因：词频越高的话，在正样本中出现次数多，那么靠正样本就能很好的学习到高频词的特征，那么负采样应该更关注于低频词。但另外一个角度，如果词频高的词经常出现在正样本，那么模型就会很容易记住这些正样本，那么模型每次都判断这些高频热点词为正，所以这时候，负采样高频词就是在适当的时候告诉模型“不是每一次这些词都是正样本“

这个概率用一个公式表示，每个词给了一个和它频率相关的权重。这个概率公式为：
$$P(w_i)=\frac{f(w_i{)}^{0.75}}{{\sum }_{j=0}^n(f(w_i{)}^{0.75})}$$
在paper中说0.75这个超参是试出来的，这个函数performance比其他函数好

在实现的过程中，通常会让模型接收3个tensor输入：

1. 代表中心词的tensor：假设我们称之为V，一般来说，这个tensor是一个形状为[batch_size, vocab_size]的one-hot tensor

2. 代表目标词的tensor：假设我们称之为T，一般来说，这个tensor同样是一个形状为[batch_size, vocab_size]的one-hot tensor

3. 代表目标词标签的tensor：假设我们称之为L，一般来说，这个tensor是一个形状为[batch_size, 1]的tensor，每个元素不是0就是1（0：负样本，1：正样本）。

模型训练过程如下：

1. 用V去查询W0，用T去查询W1，分别得到两个形状为[batch_size, embedding_size]的tensor，记为H1和H2。

2. 将这两个tensor进行点积运算，结果的形状为[batch_size]

3. 使用sigmoid函数作用在O上，将上述点积的结果归一化为一个0-1的概率值，作为预测概率，根据标签信息L训练这个模型即可。

在结束模型训练之后，一般使用W0作为最终要使用的词向量，用W0的向量表示。通过向量点乘的方式，计算不同词之间的相似度。

使用pytorch实现Skip-gram

以“the quick brown fox jumped over the lazy dog”这句话为例，我们要构造一个上下文单词与目标单词的映射关系，以quick为目标单词，假设滑动窗口大小为 1，也就是左边和右边各取 1 个单词作为上下文，这里是the和brown，可以构造映射关系：(the, quick)，(brown, quick)，这样我们就构造出两个正样本。

此外，对于这个滑动窗口外的其他单词，我们需要构造负样本，但是负样本可以是滑动窗口之外的所有单词。为了减少训练的时间，我们对负样本进行采样 k 个，称为 Negative Sampling。如 k=2，就是对每个正样本，分别构造两个负样本；例如对于(the, quick)，采样两个负样本 (lazy , quick)，(dog, quick)。

Negative Sampling 的损失函数表示如下：

在文本中，如the、a等词出现频率很高，但是对训练词向量没有太大帮助，为了平衡常见词和少见的词之间的频次，论文中以一定概率丢弃单词，计算公式如下：
$$P(w_i)=1-\sqrt{\frac{t}{f(w_i)}}$$
其中 f(w_i) 表示单词的频率，而 t 是超参数，一般 t=1e−5。使用这个公式，那些频率超过 1e−5 的单词就会被下采样，同时保持频率大小关系不变。

在负采样时，按照频率来采样单词会导致某些单词次数过多，而少见的单词采样次数过少。论文将词频按照如下公式转换：
$$P(w_i)=\frac{f(w_i{)}^{0.75}}{{\sum }_{j=0}^n(f(w_i{)}^{0.75})}$$
按照转换后的词频采样单词，使得最常见的词采样次数减少了，而最少见的词采样次数增加了。

参考论文：Distributed Representations of Words and Phrases and their Compositionality

import os
import pickle
import random
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils import data
from pkl import ws, MAX_LEN
from datetime import datetime
from tqdm import tqdm
from torch import optim
import dataset

'''
collections:
    This module implements specialized container datatypes providing alternatives to Python's general purpose built-in containers, dict, list, set, and tuple.
zipfile:
    Read and write ZIP files.
urllib:
    This module is used to operate the URL of the web page, and to grasp the content of the web page.
'''

# set up parameters
VOCABULARY_DIM = len(ws)
EMBEDDING_DIM = 128  # the dimension of word vector
EPOCH = 1000  # the number of training
BATCH_SIZE = 5  # the size of each batch of training data
NEG_SAMPLES = 3  # the size of negative samples
WINDOW_SIZE = 5  # context window
FREQUENCY = 5  # the minimum number of term frequency
DELETE_WORDS = False  # whether delete part of the words of high frequecy or not

device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')

data_path = '../01循环神经网络/aclImdb'


def read_mode(mode):
    if mode == 'train':
        text_path = [os.path.join(data_path, i) for i in ['train/neg', 'train/pos']]
    else:
        text_path = [os.path.join(data_path, i) for i in ['test/neg', 'test/pos']]

    file_path = []

    for i in text_path:
        file_path.extend([os.path.join(i, j) for j in os.listdir(i)])

    mode_text = []
    for file in tqdm(file_path):
        text = dataset.tokenize(open(file, errors='ignore').read().strip())
        mode_text.extend(text)

    return mode_text


# words = read_mode('test')

# pickle.dump(words,open('./model/train_text.pkl','wb'))
# pickle.dump(words,open('./model/test_text.pkl','wb'))

words = pickle.load(open('./model/train_text.pkl', 'rb'))

# calculate the frequency of 'UNK'
count = dict(sorted(list(ws.count.items()), key=lambda x: x[1], reverse=True))
print(f'过滤掉高频词和低频词，剩下的词语出现的总数：{np.sum(list(count.values()))}')
# np.sum(): Sum of array elements over a given axis.
count['UNK'] = len(words) - np.sum(list(count.values()))

print(f'训练集中词语的出现总数：{len(words)}')
print(f"UNK出现的总数：{count['UNK']}")

# calculate the term frequency
total_count = len(words)
word_frequency = {w: c / total_count for w, c in ws.total_count.items()}

# with a certain probability, the word of most frequent are eliminated
if DELETE_WORDS:
    t = 1e-5
    probability_drop = {w: 1 - np.sqrt(t / word_frequency[w]) for w in words}

    '''
    平衡常见词和少见的词之间的频次，以一定的概率丢弃单词
    '''
    words = [w for w in words if random.random() < (1 - probability_drop[w])]

words2idx = ws.transform(words)

# calculate the term frequency transforming three fourth to the power in terms of original paper
'''
在负采样时，按照频率来采样单词会导致某些单词次数过多，而少见的单词采样次数过少
'''
word_count = np.array([c for c in count.values()], dtype=np.float32)
word_freq = word_count / np.sum(word_count)
word_freq = word_freq ** (3 / 4)
word_freq = word_freq / np.sum(word_freq)


class WordEmbeddingDataset(data.Dataset):
    def __init__(self, word2index, frequency):
        self.word2index = torch.tensor(word2index).long()
        self.frequency = torch.Tensor(frequency)

    def __len__(self):
        return len(self.word2index)

    def __getitem__(self, index):
        center_word = self.word2index[index]  # 找到中心词
        positive_index = list(range(index - WINDOW_SIZE, index)) + list(
            range(index + 1, index + WINDOW_SIZE + 1))  # 中心词前后各C个词作为正样本
        positive_index = list(filter(lambda i: 0 <= i < len(self.word2index), positive_index))

        positive_words = self.word2index[positive_index]  # 中心词周围单词
        negative_words = torch.multinomial(self.frequency, NEG_SAMPLES * positive_words.shape[0], True)

        return center_word, positive_words, negative_words


# 构造一个神经网络，输入词语，输出词向量
class EmbeddingModule(nn.Module):
    def __init__(self, vocabulary_size, embedding_dim):
        super(EmbeddingModule, self).__init__()

        self.vocabulary_size = vocabulary_size
        self.embedding_dim = embedding_dim

        initial_range = 0.5 / self.embedding_dim

        '''
        映射目标单词的Embedding层
        '''
        self.target_embedding = nn.Embedding(self.vocabulary_size, self.embedding_dim, sparse=False)
        self.target_embedding.weight.data.uniform_(-initial_range, initial_range)  # 权重初始化的一种方式

        '''
        映射上下文单词和负样本单词的Embedding层
        '''
        self.context_negative_embedding = nn.Embedding(self.vocabulary_size, self.embedding_dim, sparse=False)
        self.context_negative_embedding.weight.data.uniform_(-initial_range, initial_range)

    def forward(self, input_label, positive_label, negative_label):
        '''
        :param input_label: [batch_size]
        :param positive_label: [batch_size, window_size*2]
        :param negative_label: [batch_size, window_size*2*NEG_SAMPLE
        :return:
        '''

        input_embedding = self.target_embedding(input_label)  # [batch_size, embedding_dim]
        positive_embedding = self.context_negative_embedding(
            positive_label)  # [batch_size, window_size*2, embedding_dim]
        negative_embedding = self.context_negative_embedding(
            negative_label)  # [batch_size, window_size*2*NEG_SAMPLE, embedding_dim]

        # 向量乘法
        input_embedding = input_embedding.unsqueeze(-1)  # [batch_size, embedding_dim, 1]
        positive_dot = torch.bmm(positive_embedding, input_embedding).squeeze(-1)  # [batch_size, window_size*2]
        negative_dot = torch.bmm(negative_embedding, input_embedding).squeeze(
            -1)  # [batch_size, window_size*2*NEG_SAMPLE]

        log_positive = F.logsigmoid(positive_dot).sum(1)
        log_negative = F.logsigmoid(negative_dot).sum(1)

        loss = -(log_positive + log_negative)  # [batch_size]
        return loss

    def get_input_embedding_weight(self):
        # 取出self.target_embedding中的数据参数
        return self.target_embedding.weight.data.gpu().numpy()


# 构造dataset和dataloader
dataset = WordEmbeddingDataset(word2index=words2idx, frequency=word_freq)

dataloader = data.DataLoader(dataset, batch_size=BATCH_SIZE, shuffle=True)

module = EmbeddingModule(VOCABULARY_DIM, EMBEDDING_DIM).to(device)
optimizer = optim.Adam(module.parameters(), lr=0.001)

for epoch in range(EPOCH):
    print(f"{'-' * 20}epoch: {epoch}{'-' * 20}")

    for i, (input_labels, positive_labels, negative_labels) in enumerate(dataloader):
        input_labels = input_labels.long().to(device)
        positive_labels = positive_labels.long().to(device)
        negative_labels = negative_labels.long().to(device)

        optimizer.zero_grad()
        loss = module(input_labels, positive_labels, negative_labels).mean()
        loss.backward()
        optimizer.step()

        if i % 100 == 0:
            print(f'loss:{loss.item()}')

    embedding_weights=module.get_input_embedding_weight()

    # Save an array to a binary file in NumPy `.npy` format.
    np.save(f'embedding-{EMBEDDING_DIM}.npy',embedding_weights)
    torch.save(module.state_dict(),f'embedding-{EMBEDDING_DIM}.nth')

代码中用到的.py文件

pkl.py：

import pickle

ws = pickle.load(open('./model/ws.pkl', 'rb'))
MAX_LEN = 20

dataset.py：

import torch
from torch.utils.data import DataLoader, Dataset
import os
import re

# 1、define the function of tokenize
def tokenize(text):
    filters = ['!', '"', '#', '$', '&', '\(', '\)', '\*', '\+', ',', '-',
               '\.', '/', ':', ';', '<', '=', '>', '\?', '@', '\[', '\\', '\]', '^',
               '_', '`', '\{', '\|', '\|', '~', '\t', '\n', '\x97', '\x96']
    text = re.sub('<.*?>', ' ', text, flags=re.S)
    text = re.sub('|'.join(filters), ' ', text, flags=re.S)

    return [i.strip() for i in text.split()]

word_sequence.py：

import numpy as np


class Word2Sequence():
    UNK_TAG = 'UNK'
    PAD_TAG = 'PAD'

    UNK = 0
    PAD = 1

    def __init__(self):
        self.dict = {
            self.UNK_TAG: self.UNK,
            self.PAD_TAG: self.PAD
        }

        self.padding = False

        # count the number of times each word appears
        self.count = {}

        self.total_count={}

    # get index corresponding to the specific word
    def word_to_index(self, word):
        # word->index
        assert self.padding == True, 'please carry on padding operation firstly'
        return self.dict.get(word, self.UNK)

    # get word corresponding to the specific index
    def index_to_word(self, index):
        # index->word
        assert self.padding == True, 'please carry on padding operation firstly'
        if index in self.inverse_dict:
            return self.inverse_dict.get(index)
        return self.UNK_TAG

    # save a single sentence to the dictionary
    def fit(self, sentence):
        '''
        :param sentence: [word1, word2, ...]
        :return:
        '''
        for word in sentence:
            self.count[word] = self.count.get(word, 0) + 1
            self.total_count[word] = self.count.get(word, 0) + 1

    # filter the word of low frequency and high frequency and generate the dictionary of word to index
    def build_dictionary(self, min_count=1, max_count=None, max_feature=None):
        '''
        :param min_count: minimum number of occurrences
        :param max_count: maximum number of occurrences
        :param max_feature: the maximum number of words contained in the dictionary
        :return:
        '''

        # filter the word of low frequency
        if min_count is not None:
            self.count = {k: v for k, v in self.count.items() if v >= min_count}

        # filter the word of high frequency
        if max_count is not None:
            self.count = {k: v for k, v in self.count.items() if v <= max_count}

        # limit the maximum amount
        if isinstance(max_feature, int):
            # items(): a set-like object providing a view on dictionary's keys
            # Return a new list containing all items from the iterable in ascending order
            self.count = sorted(list(self.count.items()), key=lambda x: x[1])

            if max_feature is not None and len(self.count) > max_feature:
                self.count = self.count[-int(max_feature):]
            for word in self.count:
                self.dict[word] = len(self.dict)
        else:
            for word in self.count:
                self.dict[word] = len(self.dict)

        self.padding = True

        # the dictionary of index to word
        self.inverse_dict = dict(zip(self.dict.values(), self.dict.keys()))

    # limit the length of sentences and transform word in sentences to corresponding index
    def transform(self, sentence, max_len=None):
        assert self.padding == True, 'please carry on padding operation firstly'

        if max_len is not None:
            sentence_index = [self.PAD] * max_len
            for index, word in enumerate(sentence[:max_len]):
                sentence_index[index] = self.word_to_index(word)
        else:
            sentence_index = [self.PAD] * len(sentence)
            for index, word in enumerate(sentence):
                sentence_index[index] = self.word_to_index(word)


        return np.array(sentence_index, dtype=np.int64)

    # realize the function transforming the index in indices to word, finally generate the list of words
    def inverse_transform(self, indices):
        '''
        :param indices: [1,2,3, ...]
        :return: [word1, word2, ...]
        '''
        sentence = []

        for index in indices:
            word = self.index_to_word(index)
            sentence.append(word)

        return sentence

    def __len__(self):
        return len(self.dict)


if __name__ == '__main__':
    ws = Word2Sequence()

    ws.fit(['唐', '舞', '桐'])

    ws.build_dictionary()

    print(ws.dict)
    print(ws.transform(['舞', '桐']))

save.py：

from word_sequence import Word2Sequence
import pickle
import os
from dataset import tokenize
from tqdm import tqdm

if __name__ == "__main__":
    if not os.path.exists('./model'):
        os.mkdir('./model')

    ws = Word2Sequence()

    path = r'../01循环神经网络/aclImdb/train'
    data_path = [os.path.join(path, 'neg'), os.path.join(path, 'pos')]

    for path in data_path:
        filename = os.listdir(path)

        file_path = [os.path.join(path, i) for i in filename if i.endswith('.txt')]

        for file in tqdm(file_path):
            sentence = tokenize(open(file, errors='ignore').read())
            ws.fit(sentence)

    # filter the word of low frequency and high frequency and generate the dictionary of word to index
    ws.build_dictionary(min_count=5)
    pickle.dump(ws, open('./model/ws.pkl', 'wb'))

本文中所使用的数据集下载地址：https://ai.stanford.edu/~amaas/data/sentiment/

补充

交叉熵

交叉熵（cross entropy）是深度学习中常用的一个概念，一般用来求目标与预测值之间的差距。

信息论

交叉熵是信息论中的一个概念，要想了解交叉熵的本质，需要先从最基本的概念讲起

信息量

首先是信息量。假设我们听到了两件事，分别如下：

• 事件A：巴西队进入了2026世界杯决赛圈。
• 事件B：中国队进入了2026世界杯决赛圈。

仅凭直觉来说，显而易见事件B的信息量比事件A的信息量要大。究其原因，是因为事件A发生的概率很大，事件B发生的概率很小。所以当越不可能的事件发生了，我们获取到的信息量就越大。越可能发生的事件发生了，我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。

假设X是一个离散型随机变量，其取值集合为χ,概率分布函数p(x)=Pr(X=x),x∈χ,则定义事件X=x0的信息量为：

$$I(x_0)=-log(p(x_0))$$

熵

考虑另一个问题，对于某个事件，有n种可能性，每一种可能性都有一个概率p(xi)，这样就可以计算出某一种可能性的信息量。举一个例子，假设你拿出了你的电脑，按下开关，会有三种可能性，下表列出了每一种可能的概率及其对应的信息量

序号	事件	概率p	信息量I
A	电脑正常开机	0.7	-log(p(A))=0.36
B	电脑无法开机	0.2	-log(p(B))=1.61
C	电脑爆炸了	0.1	-log(p©)=2.30

我们现在有了信息量的定义，而熵用来表示所有信息量的期望，即：

$$H(X)=-\sum _{i=1}^{n}p(x_i)log(p(x_i))$$

其中n代表所有的n种可能性，所以上面的问题结果就是：

相对熵

相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度来衡量这两个分布的差异

在机器学习中，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]

KL散度的计算公式：
$$D_{KL}(p||q)=\sum _{i=1}^{n}log(\frac{p(x_i)}{q(x_i)})$$

n为事件的所有可能性，D_KL的值越小，表示q分布和p分布越接近

交叉熵

将相对熵的公式进行变形：
$$D_{KL}(p||q)=\sum _{i=1}^{n}p(x_i)log(p(x_i))-\sum _{i=1}^{n}p(x_i)log(q(x_i))=-H(p(x))+[-\sum _{i=1}^{n}p(x_i)log(q(x_i))]$$

等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵：

$$H(p,q)=-\sum _{i=1}^{n}p(x_i)log(q(x_i))$$

在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好。由于KL散度中的前一部分−H(y)不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss，评估模型。

机器学习中交叉熵的应用

为什么要用交叉熵做loss函数？

在线性回归问题中，常常使用MSE（Mean Squared Error）作为loss函数，比如：
$$loss=\frac{1}{2m}\sum _{i=1}^m(y_i-\widetilde{y_i}{)}^2$$

这里的m表示m个样本的，loss为m个样本的loss均值。

MSE在线性回归问题中比较好用，那么在逻辑分类问题中还是如此么？

交叉熵在单分类问题中的使用

这里的单类别是指，每一张图像样本只能有一个类别，比如只能是狗或只能是猫。

交叉熵在单分类问题上基本是标配的方法：
$$loss=-\sum _{i=1}^n{y}_{i}log(\widetilde{y_i})$$

举例说明,比如有如下样本：

对应的标签和预测值：

*	猫	青蛙	老鼠
Label	0	1	0
Pred	0.3	0.6	0.1

那么：

对应一个batch的loss就是：
$$loss=-\frac{1}{m}\sum _{j=1}^m\sum _{i=1}^n{y}_{ji}log(\widetilde{y_{ji}})$$

m为当前batch的样本数

交叉熵在多分类问题中的使用

这里的多类别是指，每一张图像样本可以有多个类别，比如同时包含一只猫和一只狗，和单分类问题的标签不同，多分类的标签是n-hot。

比如下面这张样本图，即有青蛙，又有老鼠，所以是一个多分类问题

对应的标签和预测值：

*	猫	青蛙	老鼠
Label	0	1	1
Pred	0.1	0.7	0.8

值得注意的是，这里的Pred不再是通过softmax计算的了，这里采用的是sigmoid。将每一个节点的输出归一化到[0,1]之间。所有Pred值的和也不再为1。换句话说，就是每一个Label都是独立分布的，相互之间没有影响。所以交叉熵在这里是单独对每一个节点进行计算，每一个节点只有两种可能值，所以是一个二项分布。

二项分布中，交叉熵的计算可以简化：
$$loss=-ylog(\tilde{y})-(1-y)log(1-\tilde{y})$$

注意，上式只是针对一个节点的计算公式。这一点一定要和单分类loss区分开来。

例子中可以计算为：

$$单张样本的loss即为：loss=los{s}_{猫}+los{s}_{蛙}+los{s}_{鼠}$$
每一个batch的loss就是：
$$loss=\sum _{j=1}^m\sum _{i=1}^n-y_{ji}log(\widetilde{y_{ji}})-(1-y_{ji})log(1-\widetilde{y_{ji}})$$

式中m为当前batch中的样本量，n为类别数

torch.multinominal()采样函数

torch.multinominal()方法可以根据给定权重对数组进行多次采样，返回采样后的元素下标

参数：

• input ：权重（必须是torch.Tensor格式），也就是取每个值的概率，可以是1维或2维。可以不进行归一化。
• num_samples ： 采样的次数。如果input是二维的，则表示每行的采样次数
• replacement ：默认值值是False，即不放回采样。如果replacement =False，则num_samples必须小于input中非零元素的数目。

按权重采样

从四个元素中随机选择一个，每个元素被选择到的概率分别为：[0.2, 0.2, 0.3, 0.3]：

import torch

weights = torch.Tensor([0.1, 0.2, 0.3, 0.4])
index = torch.multinomial(weights, 1)
print(index) # index的值可能是：torch([0])

按频率采样

multinomial()函数的input可以是大于1的数，在函数内部会再次进行归一化。

例如在处理文本对word进行采样时，直接传入词典中每个词的词频就好了

import torch

weights = torch.Tensor([3, 2, 7, 8])
index = torch.multinomial(weights, 1)
print(index) # index的值可能是：torch([1])

有放回采样

设置replacement=True，可以进行有放回的采样，此时的n_sample参数可以大于input的长度：

import torch

weights = torch.Tensor([0, 0.3, 0.7])
index = torch.multinomial(weights, 10, replacement=True)
print(index) # index的值可能是：tensor([2, 2, 2, 2, 2, 1, 1, 2, 2, 1])

权重为0的元素

如果是无放回的采样，input中值为0的元素只有在其他元素都被抽到后，才会被抽到；

如果是有放回的采样，input中值为0的元素永远不会被抽到。

import torch

weights = torch.Tensor([0, 0.3, 0.7])
index = torch.multinomial(weights, 3)
print(index) # index的值可能是：tensor([1, 2, 0])

多行同时进行采样

传入的input可以是2维矩阵，此时会分别对每一行按各自的权重进行采样：

import torch

weights = torch.Tensor([
    [0, 0.3, 0.7],
    [0.3, 0.7, 0]
])
index = torch.multinomial(weights, 2)
print(index) 

'''
index的值可能是： tensor([[2, 1],
        [1, 0]])
'''

参考

1、余弦相似性

2、使用余弦相似度算法计算文本相似度

3、[word2vec词向量模型]原理详解+代码实现

4、[NLP] 秒懂词向量Word2vec的本质

5、一文搞懂交叉熵在机器学习中的使用，透彻理解交叉熵背后的直觉

6、Word Embedding的发展和原理简介

7、Tag: Continuous Bag of Words (CBOW)

8、一文弄懂Word2Vec之skip-gram（含详细代码）

9、Negative Sampling

10、Pytorch小抄：multinominal采样函数

11、PyTorch 实现 Skip-gram