深度学习：NiN（Network In Network）详细讲解与代码实现

网络核心思想

LeNet、AlexNet和VGG都有一个共同的设计模式：通过一系列的卷积层与汇聚层来提取空间结构特征；然后通过全连接层对特征的表征进行处理。
AlexNet和VGG对LeNet的改进主要在于如何扩大和加深这两个模块。
或者，可以想象在这个过程的早期使用全连接层。然而，如果使用了全连接层，可能会完全放弃表征的空间结构。
网络中的网络（NiN）提供了一个非常简单的解决方案：在每个像素的通道上分别使用多层感知机 [Lin et al., 2013]

1*1卷积

1 * 1卷积实际上就是对特征图所有channel对应的像素点做全连接网络，由于它只考虑了1个像素点，它不像3 * 3卷积那样可以考虑周围像素点，但是可以让特征图在不需要padding的情况下保证的H、W不变，也就是融合了买个像素点不同通道的特征所以它也有跨通道交融的作用。卷积核的数量决定了输出的维度，所以用1 * 1卷积只会改变特征图的channel数，这也就是1 * 1卷积有升维 、降维的作用，在维度降低的同时，计算量也就减少了，模型速度会变快，与此同时，它在保留了空间信息的同时，还增加了非线性激活函数，非线性激活函数可以增加模型的复杂程度，让模型逼近更复杂的曲线。

NiN块的作用

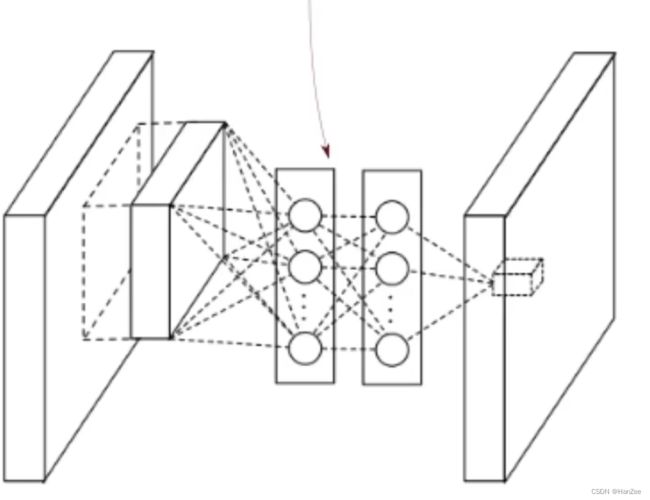
NiN是由AlexNet改进而来的，他的主要贡献是提出了NiN块这个概念，随着网络层数的加大，参数的数量也水涨船高，我们举一个例子：

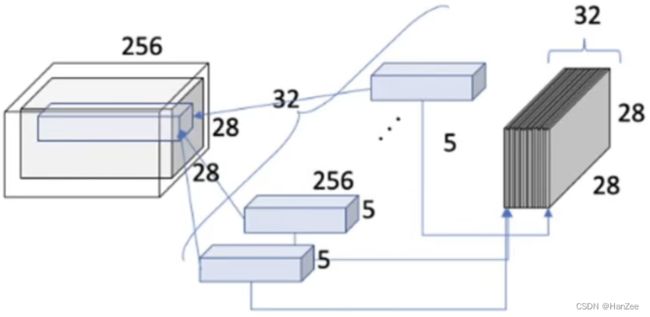
假设现在特征图是 28 * 28 * 256，我们想把它变成28 * 28 *32
我们的原始方法是采用32个 5 * 5的卷积核。如上图，那么它的参数量就是：
$5\ast 5\ast 32\ast 256+32=20182$
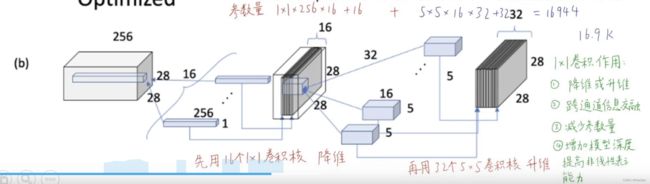
而我们的NiN块的核心思想是把原始特征图先降维在升维，也就是我把32个 5 * 5卷积核替换成先经过16个 1 * 1的卷积核，特征图就变成了， 28 * 28 *16 ，然后在经过一个32个 5 * 5 的卷积核，它的参数数量为：
$1\ast 1\ast 16\ast 256+16=4112$
$5\ast 5\ast 32\ast 16+32=12832$
求和也就是16944，参数量对比之前少了15%左右。

全局池化（Global Average Pooling）

在NiN网络中，去掉了卷积层后面的全连接层，加入与了全局池化层，全局池化层是把最后的特征图数量变成了分类的数量，这样的可解释性更强，之后，我们只需要对每一个channel求一个全局平均值，然后经过，Softmax分类，这样也大大减少了参数量。

基于NiN的服装分类（Pytorch）

服装分类数据集

我们可以通过框架中的内置函数将Fashion-MNIST数据集下载并读取到内存中。

# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式，
# 并除以255使得所有像素的数值均在0到1之间
def load_data_fashion_mnist(batch_size, resize=None):  #@save
    """下载Fashion-MNIST数据集，然后将其加载到内存中"""
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)#通过compose组合多个操作
    mnist_train = torchvision.datasets.FashionMNIST(
        root="../data", train=True, transform=trans, download=True)
    mnist_test = torchvision.datasets.FashionMNIST(
        root="../data", train=False, transform=trans, download=True)
    return (data.DataLoader(mnist_train, batch_size, shuffle=True,
                            num_workers=4),
            data.DataLoader(mnist_test, batch_size, shuffle=False,
                            num_workers=4))
                            #num workers 为线程数

定义模型

def nin_block(in_channels, out_channels, kernel_size,strides, padding):
    return nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
        nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1),
        nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1),
        nn.ReLU()
    )

net = nn.Sequential(
    nin_block(1, 96, kernel_size=11, strides=4, padding=0),
    nn.MaxPool2d(3, stride=2),
    nin_block(96, 256, kernel_size=5, strides=1, padding=2),
    nn.MaxPool2d(3, stride=2),
    nin_block(256, 384, kernel_size=3, strides=1, padding=1),
    nn.MaxPool2d(3, stride=2),
    nn.Dropout(0.5),
    # 标签类别数是10
    nin_block(384, 10, kernel_size=3, strides=1, padding=1),
    nn.AdaptiveAvgPool2d((1, 1)),
    # 将四维的输出转成二维的输出，其形状为(批量大小,10)
    nn.Flatten())
    

测试数据

def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
    """使用GPU计算模型在数据集上的精度"""
    if isinstance(net, nn.Module):
        net.eval()  # 设置为评估模式
        if not device:
            device = next(iter(net.parameters())).device
    # 正确预测的数量，总预测的数量
    metric = d2l.Accumulator(2)#累加器
    
    with torch.no_grad():#禁止计算梯度
        for X, y in data_iter:
            if isinstance(X, list):
                # BERT微调所需的（之后将介绍）
                X = [x.to(device) for x in X]
            else:
                X = X.to(device)
            y = y.to(device)
            metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

训练模型

#@save
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
    """用GPU训练模型(在第六章定义)"""
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    print('training on', device)
    net.to(device)
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])
    timer, num_batches = d2l.Timer(), len(train_iter)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，样本数
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()#更新参数
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (train_l, train_acc, None))
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch + 1, (None, None, test_acc))
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
          f'on {str(device)}')

train_iter, test_iter = load_data_fashion_mnist(256, resize=224)
train_ch6(net, train_iter, test_iter, 10, 0.01, d2l.try_gpu())