【数据结构与算法】之多指针算法

前言

本文为 【数据结构与算法】多指针算法 相关知识，下边将对链表反转（包含迭代反转链表、递归反转、头插法反转），双指针-快慢指针（包含寻找单向无环链表的中点、判断单向链表是否有环及找环入口），双指针-左右指针（包含两数之和、二分查找）等相关多指针算法进行详尽介绍~

博主主页：小新要变强 的主页
Java全栈学习路线可参考：【Java全栈学习路线】最全的Java学习路线及知识清单，Java自学方向指引，内含最全Java全栈学习技术清单~
算法刷题路线可参考：算法刷题路线总结与相关资料分享，内含最详尽的算法刷题路线指南及相关资料分享~
Java微服务开源项目可参考：企业级Java微服务开源项目（开源框架，用于学习、毕设、公司项目、私活等，减少开发工作，让您只关注业务！）

---

目录

一、链表反转

链表反转公用代码：

public class ReverseLink {
    public static void main(String[] args) {
     
    }

    // 遍历的方法
    public static void print(Node<Integer> head) {
        Node<Integer> current = head;
        while (current != null) {
            System.out.println(current.t);
            current = current.next;
        }
    }

    private static class Node<T> {
        private T t;
        private Node<T> next = null;

        public Node(T t) {
            this.t = t;
        }
    }


    private static Node<Integer> buildLink() {
        Node<Integer> head = new Node<>(1);
        Node<Integer> node2 = new Node<>(2);
        Node<Integer> node3 = new Node<>(3);
        Node<Integer> node4 = new Node<>(4);
        Node<Integer> node5 = new Node<>(5);

        head.next = node2;
        node2.next = node3;
        node3.next = node4;
        node4.next = node5;
        return head;
    }

}

1️⃣迭代反转链表

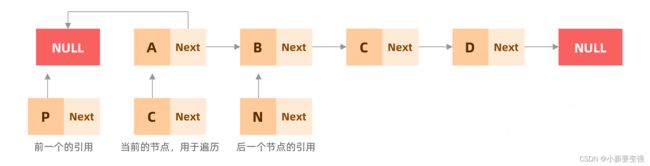
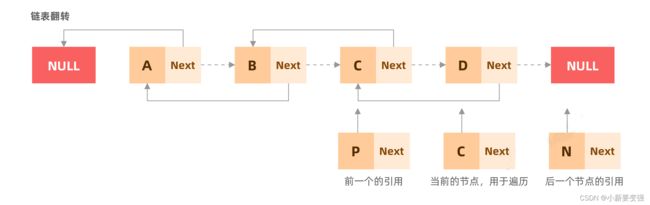
链表翻转最大的问题就是，对于单链表而言，引用一旦指向新的节点，就会于之前关联的节点失去联系，所以我们可以使用三个引用临时保存需要操作的节点：

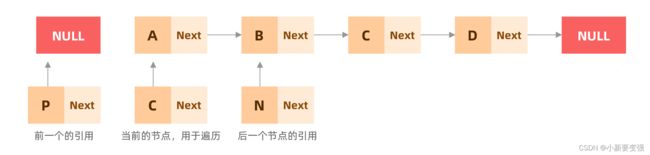
• 第一个和第二个引用用来进行反转操作
• 第三个引用用来保存后边的节点，防止关联失效

• 以后每一步操作，只需要将三个临时节点统一向后移动即可，这就是一个遍历的过程

代码如下：

// 采用单个指针的方式，迭代进行逆转
public static Node<Integer> reverseLink(Node<Integer> head) {

    if (head == null || head.next == null) {
        return head;
    }

    // 定义三个引用，分别代表当前节点，以及他的前后节点
    Node<Integer> prevNode = null;
    Node<Integer> current = head;
    Node<Integer> nextNode = head.next;

    // 先进行一个翻转翻转
    current.next = prevNode;

    while (nextNode != null) {

        // 三个指针,统一移动
        prevNode = current;
        current = nextNode;
        nextNode = current.next;

        // 翻转
        current.next = prevNode;

        // 确定到达尾部，定义新的头结点
        if (nextNode == null) {
            head = current;
        }
    }
    return head;
}

2️⃣递归反转

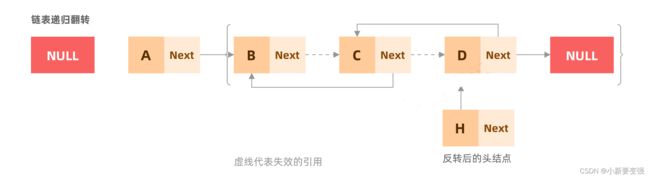
• 递归翻转的思路和之前的思路恰好相反，递归往往都是这个样子：

• 我们使用递归将后续的节点成功反转：

• 接下来只需要将A和B反转即可。

代码如下：

// 递归遍历链表
public static Node<Integer> recursiveReverseLink(Node<Integer> head) {

    if (head == null || head.next == null) {
        return head;
    }

    // 上边的A和B的反转，node是反转后的头节点
    Node<Integer> node = recursiveReverseLink(head.next);
    head.next.next = head;
    head.next = null;

    return node;

}

3️⃣头插法反转

头插法的思路比较简单，就是从头开始遍历，每次摘下一个节点，然后使用头插法，拼接成一个新的链表：

代码如下：

// 使用头插法
public static Node<Integer> headInsertReverseLink(Node<Integer> head) {

    if (head == null || head.next == null) {
        return head;
    }

    // newHead表示的是新建的链表的头结点
    Node<Integer> newHead = null, temp;

    while (head != null) {
        // 临时节点指向head
        temp = head;
        // head后移，相当于将头结点摘除了
        head = head.next;
        temp.next = newHead;
        newHead = temp;
    }

    return newHead;
}

二、双指针-快慢指针

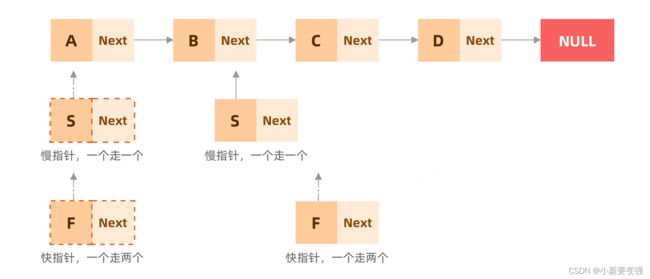
1️⃣寻找单向无环链表的中点

代码如下：

public static Node findMiddle(Node head){
    Node fast = head,slow = head;
    while (fast != null && fast.next != null){
        fast = fast.next.next;
        slow = slow.next;
    }
    return slow;
}

2️⃣判断单向链表是否有环及找环入口

题目： 给定一个单向的链表，判断该链表是否有换，如果不存在换返回null，如果存在，则返回链表开始入环的第一个节点。

说明： 不允许修改给定的链表。如下图：应该返回C这个节点。

判断有没有环思路： 我们同样使用快慢指针，fast 与slow，一旦fast追上slow就说明存在环。

寻找换的入口，是一个比较麻烦的事情，我们有基本的数学推导如下，这里有个一直条件，fast一旦追上slow说明fast比slow正好快了一圈。

如下图所示，设链表中环外部分的长度为 a。slow 指针进入环后，又走了 b 的距离与 fast 相遇。此时，fast 指针已经走完了环的 n 圈，因此它走过的总距离为 ：
$$a+(b+c)+b=a+2b+c$$

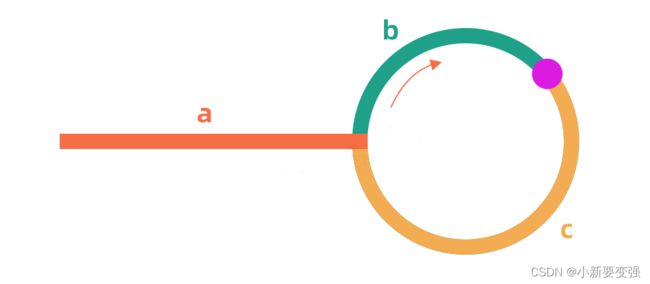
根据题意，任意时刻，fast 指针走过的距离都为 slow 指针的 2 倍。因此，我们有：
$$a+2b+c=2(a+b)⟹a=c$$ 有了这个等量关系，我们会发现：在我们的题目中，从相遇点到入环点的距离，恰好等于从链表头部到入环点的距离。

因此，当发现 slow 与 fast 相遇时，我们再额外使用一个指针 ptr。起始，它指向链表头部；随后，它和slow 每次向后移动一个位置。最终，它们会在入环点相遇。

代码如下：

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null) {
            return null;
        }
        ListNode slow = head, fast = head;
        while (fast != null) {
            slow = slow.next;
            if (fast.next != null) {
                fast = fast.next.next;
            } else {
                return null;
            }
            if (fast == slow) {
                ListNode ptr = head;
                while (ptr != slow) {
                    ptr = ptr.next;
                    slow = slow.next;
                }
                return ptr;
            }
        }
        return null;
    }
}

三、双指针-左右指针

1️⃣两数之和

输入一个【有序数组】和一个目标值，找到数组中的两个数相加等于目标值，输出两个数字的下标：

代码如下：

public int[] twoSum(int[] nums,int target){
    int left = 0,right = nums.length -1;
    while (left < right){
        int sum = nums[left] + nums[right];
        if(sum == target){
            return new int[]{left+1,right+1};
        } else if(sum < target){
            left++;
        } else if (sum > target){
            right--;
        }
    }
    return new int[]{-1,-1};
}

2️⃣二分查找

给定一个有序数组，和一个目标值，找出目标值出现的位置，返回下标，找不到则返回-1：

代码如下：

public static int binarySearch(int[] nums,int target){
    int left = 0,right = nums.length -1;
    while (left <= right){
        int middle = (left + right)/2;
        if(nums[middle] == target){
            return middle;
        } else if(nums[middle] < target){
            left = middle+1;
        } else if (nums[middle] > target){
            right = middle -1;
        }
    }
    return -1;
}

---

后记

Java全栈学习路线可参考：【Java全栈学习路线】最全的Java学习路线及知识清单，Java自学方向指引，内含最全Java全栈学习技术清单~
算法刷题路线可参考：算法刷题路线总结与相关资料分享，内含最详尽的算法刷题路线指南及相关资料分享~