《Attention Is All You Need》论文笔记 - 【transformer模型】

论文来源：NeurIPS 2017
论文链接：点击进入

 该篇论文提出了一个新颖的网络结构：Transformer。其没有使用循环递归结构和卷积结构，仅基于注意力机制。在两个机器任务上表明了模型能够更好的并行化计算，可以显著地减少训练时间，性能达到了SOTA的效果。

 【注：transformer的并行化主要体现在self-attention模块上，在encoder端其可以并行处理整个序列，而不像rnn、lstm那样要一个token一个token的从前往后计算。】
 
 

⭐整体结构概述：

 大多数神经序列转换模型都有一个encoder-decoder结构。encoder用于将符号表示的输入序列编码映射到一个连续表示的序列。然后decoder端给定一个输入，decoder结合encoder的输出每次生成一个元素的符号序列。
 transformer也是由encoder-decoder结构构成，其结构如下图所示：

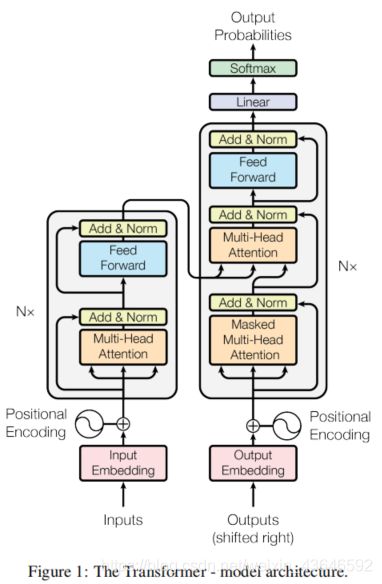
 下面我用个人的理解大致概括一下前向传播的流程，这样方便后续展开各部分讨论：
 

Encoder端处理流程：

 首先是将输入通过了embedding层，然后和位置编码的结果进行相加得到嵌入向量。然后将这个嵌入向量经过3个线性变换（可通过全连接层实现）得到Q、K、V这3个矩阵。然后Q和K矩阵点积、除dk的平方根（即缩放），再softmax得到一个注意力得分矩阵。最后乘上V矩阵即为self-attention层的结果。然后multi-head attention层的输出就是综合了多个self-attention层的结果进行concat传入全连接得到。然后经过残差和LN。然后再经过两层的全连接、残差、LN得到输出。

 【注：NLP领域不用batch normalization是因为句子长度不一致，并且各个batch的信息没啥关系，因此只考虑句子内信息的归一化，即LN】
 

Decoder端处理流程：

 利用encoder的最后一层的输出计算K、V矩阵作为每个decoder的multi-head attention层的K、V矩阵。而Q矩阵则利用decoder的masked multi-head attention层输出计算的Q矩阵。为了避免计算attention层的输出时使用到了“未来的信息”(即decoder端当前时刻往后时刻的信号)，因为从encoder得到的K、V矩阵包含了源语言的全局信息。所以可以采用论文中所说的mask机制屏蔽掉未来信息；具体操作：可以在Q、K矩阵点积缩放后，将这些需要屏蔽的信息设为负无穷，然后传入softmax后这些设为负无穷的值可以趋于0，然后再和V矩阵相乘。
 Q和K点积、缩放、屏蔽，softmax后会得到如下所示的注意力得分矩阵，横轴和为1。即被屏蔽掉的经过softmax后变为0了。

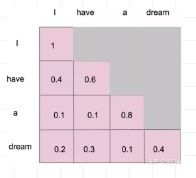
 同样，在decoder的masked multi-head attention层（其Q、K、V矩阵来自decoder的输入计算得到，没有来自encoder的信息。），训练的时候。因为考虑到利用并行计算的优势，一次性将所有目标单词预测出来，而不是一个一个单词输入，所以同样需要mask机制来处理，确保当前时刻只能利用其前面单词的的嵌入信息进行预测。
 当训练好模型预测时，decoder端一个单词一个单词输入，每次decoder都会利用前面已经解码输出的所有单词的嵌入信息来计算attention，直到预测输出终止符。
 

输出端处理流程：

 整个模型的最后经过全连接层和softmax输出各单词的概率分布。

 

 

⭐Encoder:

 encoder由6个相同的encoder层组成，每个encoder层包含2个子层：

1.多头注意力层（由self-attention组成）
2.全连接前馈神经网络

 每个子层在进行LN之前都通过一个残差操作，即如下公式：

 同时，为了方便这些残差的连接操作，transformer里的所有子层，包括embedding层的输出向量的维度都是d_model = 512。
 

⭐Decoder：

 decoder同样由6个相同的decoder层组成。但是每个decoder层包含了3个子层：

1.多头注意力层（由self-attention组成）
2.全连接前馈神经网络
3.多头注意力层（由self-attention组成，使用编码器最后一层的输出计算K、V矩阵，Q矩阵使用decoder端的）

 同encoder一样，每个子层在进行LN之前都通过一个残差操作。

 还和encoder不一样的是，对self-attention层的计算做了修改，即前面提到的mask机制，确保当前时刻只能利用其前面单词的的嵌入信息进行预测。

 

⭐Attention：

 注意力函数的输出是V矩阵所有values的加权和，这些权重是通过Q、K矩阵计算得到。
 

Scaled Dot-Product Attention：

  如下是缩放点积注意力的计算公式和结构（其中mask操作是可选择的。）：

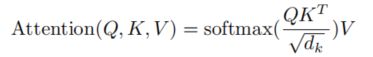
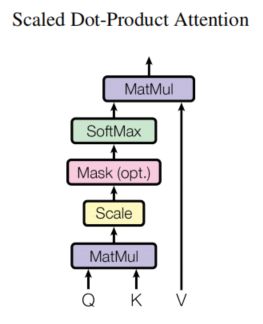
 矩阵Q、K的维度相同都是d_k（所以上面公式中将K转置了），而矩阵V的维度是d_v。

 计算注意力的方式有多种（如下），论文用的是点积，只不过加了个缩放因子。点积的好处是在计算快，空间高效，可以使用高度优化的矩阵乘法实现。论文里提到，当维度d_k较大时，加性注意力即下图的拼接权重的方式会优于点积，作者怀疑是因为当维度d_k较大时，点积的结果也变大，可能会将 Softmax 函数推入梯度极小的区域，造成反向传播梯度就会很小。所以为了抵消这个影响，作者对点积的结果加了个缩放因子。

 

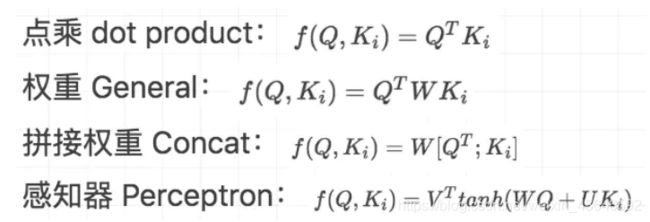
Multi-Head Attention：

 多头注意力公式和结构如下：

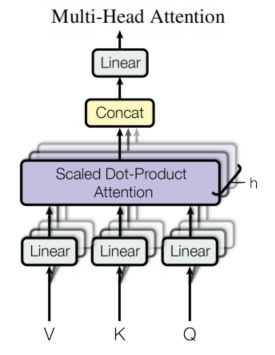
 上面图中的Q、K、V其实是上一层的输出，是相等的，维度都是d_model=512（因为transformer定义了每一层的输出维度都是512）。而作者发现，将这3个相等的矩阵通过线性层（即全连接层）分别映射为Q、K的维度为d_k，V的维度为d_v，（执行h次）这样做是有益的。然后再并行地执行缩放点积注意力，生成维度为d_v的输出。
 作者设置：h=8。并将全连接层输出设置为64，即：d_k = d_v = 64（因为d_model / h = 64）。
 最后将h=8次的操作concat后维度即为h*d_v = 8*64 = 512，还是等于512，输入和输出维度一样，最后再将concat后的结果送入一个全连接，收工~。由于前面每个全连接输出维度都减少成了64所以和单个注意力层的计算量是差不多的。
 

⭐Position-wise Feed-Forward Networks：

 除了attention层，还有个前馈神经网络层，其实就是两层的全连接层和一个ReLU激活函数层，第一层的输入输出维度是512、2048。第二层的输入输出维度是2048、512。

 

⭐Embeddings and Softmax：

 和其他一些序列转换模型一样，作者使用了可以学习的embedding层（就像torch里的nn.embedding）将输入token映射成维度为d_model=512的向量，并乘上d_model的平方根。在输出层使用全连接层和softmax输出下一token的概率分布。在两个embedding层之间和pre-softmax线性变换之间共享相同的权重。

 

⭐Positional Encoding：

 由于transformer没有循环递归结构和卷积结构，所以为了能够使用到序列的顺序信息，就必须在embedding中注入各token在序列中的相对或绝对位置的信息。所以作者结合了positional encoding信息到input embedding中。这个位置编码和输入embedding一样也是维度为d_model吗，这样就能将它们相加来结合。
 位置编码有可以学习的，有固定的。作者采用的是不同频率的sin,cos函数：

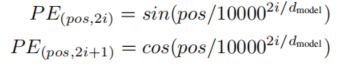
 假设有N个位置（即有N个token所以就有N个位置），每个位置都要编码成维度：512。
 则公式中的 pos 范围就是：0-N，i 的范围就是：0-511。i为偶数用sin，奇数用cos。

 作者用这个sin-cos计算位置编码的原因是，由于pos+k位置的编码PE可以用pos位置编码线性表示：

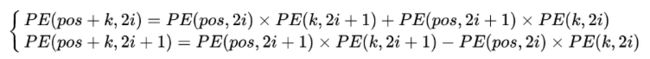
 这样的信息，等价于在告诉模型，token之间的相对位置信息。
 且这种位置编码有个好处就是，可以扩展到在遇到比训练时候的序列还要长的情况。

 

⭐Why self-attention?

 self-attention的好处就是能够一步到位计算，即捕捉到全局的联系，解决了长距离依赖。不像循环结构那样，要一步步递推、更新状态，这个path越长，遗忘的前面的信息就越多。也不想卷积那样要增加卷积核来扩大感受野才能捕捉到尽可能多的信息。self-attention相当于把序列两两比较（即那个Q、K点积的操作。）
 以下为self-attention和循环结构和卷积结构的情况对比，可以看到self-attention的优势很明显。

⭐实验部分：

 介绍了数据集、硬件环境、优化器的设置、dropout、LN、Label Smoothing。

 在两个机器翻译数据集上对比了模型的性能，transformer用了最少的资源达到了SOTA的效果。

 且对模型自身的一些参数进行测试，看哪些参数对模型影响较大。

【1】3W字长文带你轻松入门视觉Transformer
【2】细讲 | Attention Is All You Need
【3】[论文解读]Attention is all you need
【4】论文解读:Attention is All you need
【5】transformer面试题的简单回答