Scipy.integrate(scipy积分部分中文文档翻译,进度70%)
文章目录
-
-
- 积分(scipy.integrate)
- 通用积分(quad)
- 一般多重积分(dblquad,tplquad,nquad)
- 高斯正交
- Romberg积分
- 使用采样数据进行积分
- 使用低级回调函数加快积分<未翻译>
- 常微分方程(solve_ivp)
- 用带状雅可比矩阵求解系统<未翻译完>
-
对应链接:
积分(scipy.integrate)
该scipy.integrate子程序包提供了几种积分方法,包括普通的微分方程积分器。help命令提供了该模块的概述:
>>> help(integrate)
Methods for Integrating Functions given function object.
quad -- General purpose integration.
dblquad -- General purpose double integration.
tplquad -- General purpose triple integration.
fixed_quad -- Integrate func(x) using Gaussian quadrature of order n.
quadrature -- Integrate with given tolerance using Gaussian quadrature.
romberg -- Integrate func using Romberg integration.
Methods for Integrating Functions given fixed samples.
trapz -- Use trapezoidal rule to compute integral from samples.
cumtrapz -- Use trapezoidal rule to cumulatively compute integral.
simps -- Use Simpson's rule to compute integral from samples.
romb -- Use Romberg Integration to compute integral from
(2**k + 1) evenly-spaced samples.
See the special module's orthogonal polynomials (special) for Gaussian
quadrature roots and weights for other weighting factors and regions.
Interface to numerical integrators of ODE systems.
odeint -- General integration of ordinary differential equations.
ode -- Integrate ODE using VODE and ZVODE routines.
通用积分(quad)
quad适用于一个函数在数轴上两个点之间积分的这一情况。当然了,对于特殊情况,这个积分函数的积分限也可以设置为无穷。
例如,假设您希望在区间[0,4.5]上面积分一个贝塞尔函数jv(2.5, x),公式如下:
I = ∫ 0 4.5 J 2.5 ( x ) d x I=\int_0^{4.5}J_{2.5}(x)dx I=∫04.5J2.5(x)dx
可以使用quad进行计算:
>>> import scipy.integrate as integrate
>>> import scipy.special as special
>>> result = integrate.quad(lambda x: special.jv(2.5,x), 0, 4.5)
>>> result
(1.1178179380783249, 7.8663172481899801e-09)
>>>
>>> from numpy import sqrt, sin, cos, pi
>>> I = sqrt(2/pi)*(18.0/27*sqrt(2)*cos(4.5) - 4.0/27*sqrt(2)*sin(4.5) +
... sqrt(2*pi) * special.fresnel(3/sqrt(pi))[0])
>>> I
1.117817938088701
>>> print(abs(result[0]-I))
1.03761443881e-11
quad的第一个参数是可调用的Python对象(即函数,方法或类实例)。注意,在以上例子中,我们使用了lambda函数作为参数。接下来的两个参数是积分的上下极限。
返回值是一个元组tuple,第一个元素保存积分的估计值,第二个元素保存误差的上限。注意,在这种情况下,该积分的真实值为
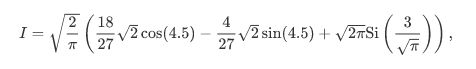
其中
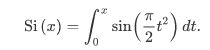
是菲涅耳正弦积分。请注意,数值计算的积分在 结果的精确度-远低于报告的错误范围。(这句翻译存疑)
如果要积分的函数需要其他参数,则可以在args参数中提供它们。假设应计算以下积分:
I ( a , b ) = ∫ 0 1 ( a x 2 + b x ) d x I(a,b)=\int_0^1(ax^2+bx) dx I(a,b)=∫01(ax2+bx)dx
可以使用以下代码进行求值:
>>>
>>> from scipy.integrate import quad
>>> def integrand(x, a, b):
... return a*x**2 + b
...
>>> a = 2
>>> b = 1
>>> I = quad(integrand, 0, 1, args=(a,b))
>>> I
(1.6666666666666667, 1.8503717077085944e-14)
若要输入无穷,quad可以使用 inf变量代表。例如,假设我们要对以下函数进行数值积分,其中含有无穷的情形:
E n ( x ) = ∫ 1 ∞ e − x t t n d t E_n(x)=\int_1^\infty \frac{e^{-xt}}{t^n}dt En(x)=∫1∞tne−xtdt
尽管已经有special.expn(n,x)这样简洁的表示方法,但是在这里我们不妨假设我们不幸忘掉了还有这个函数可调用,于是只好自己造轮子。
上式中被积函数部分为下面的integrand函数,而vec_expint函数则定义了积分步骤。让我们来看一下执行的结果:
>>>
>>> from scipy.integrate import quad
>>> def integrand(t, n, x):
... return np.exp(-x*t) / t**n
...
>>> def expint(n, x):
... return quad(integrand, 1, np.inf, args=(n, x))[0]
>>> vec_expint = np.vectorize(expint)
>>> vec_expint(3, np.arange(1.0, 4.0, 0.5))
array([ 0.1097, 0.0567, 0.0301, 0.0163, 0.0089, 0.0049])
>>> import scipy.special as special
>>> special.expn(3, np.arange(1.0,4.0,0.5))
array([ 0.1097, 0.0567, 0.0301, 0.0163, 0.0089, 0.0049])
使用quad积分的函数甚至在被积函数内部再次使用quad参数,相当于做一次二重积分(尽管由于使用,在积分中可能存在数值误差,因此误差范围可能会被低估)。
在这种情况下,积分是

>>> result = quad(lambda x: expint(3, x), 0, np.inf)
>>> print(result)
(0.33333333324560266, 2.8548934485373678e-09)
>>> I3 = 1.0/3.0
>>> print(I3)
0.333333333333
>>> print(I3 - result[0])
8.77306560731e-11
以上示例显示,可以通过重复调用,来处理多重积分。
一般多重积分(dblquad,tplquad,nquad)
双重和三重积分的相关函数由dblquad和tplquad实现。这些函数表示积分上下限入口参数为4或6个,分别对应二重或者三重积分。所有内部积分的上下限都需要定义为函数。

依旧以上面的函数为例,双重积分计算多个值的示例如下图所示:
>>> from scipy.integrate import quad, dblquad
>>> def I(n):
... return dblquad(lambda t, x: np.exp(-x*t)/t**n, 0, np.inf, lambda x: 1, lambda x: np.inf)
>>> print(I(4))
(0.2500000000043577, 1.29830334693681e-08)
>>> print(I(3))
(0.33333333325010883, 1.3888461883425516e-08)
>>> print(I(2))
(0.4999999999985751, 1.3894083651858995e-08)
以上二重积分极限为定值。而作为非恒定极限的示例,请考虑积分

可以使用以下表达式计算此积分(注意,对于内部积分的上限,请使用非恒定Lambda函数):
>>> from scipy.integrate import dblquad
>>> area = dblquad(lambda x, y: x*y, 0, 0.5, lambda x: 0, lambda x: 1-2*x)
>>> area
(0.010416666666666668, 1.1564823173178715e-16)
对于n折集成,scipy提供了功能nquad。积分界限是一个可迭代的对象:常数界限的列表或非常数积分界限的函数的列表。积分的顺序(以及边界的顺序)从最里面的积分到最外面的积分。
<本段翻译存疑,未能正确翻译出来。>
上面的积分
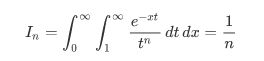
可以计算为
>>> from scipy import integrate
>>> N = 5
>>> def f(t, x):
... return np.exp(-x*t) / t**N
...
>>> integrate.nquad(f, [[1, np.inf],[0, np.inf]])
(0.20000000000002294, 1.2239614263187945e-08)
注意,f的参数顺序必须与积分边界的顺序匹配,即在内层的积分函数放在前面,外层的放在后面。可以看见公式中内层积分的范围是 [ 1 , ∞ ] [1 ,\infty] [1,∞],外层的是 [ 0 , ∞ ] [0,\infty] [0,∞],所以在代码中也是这样体现出来的。
非恒定积分范围也可以用类似的方式处理。比如以下的例子,

可以通过:
>>> from scipy import integrate
>>> def f(x, y):
... return x*y
...
>>> def bounds_y():
... return [0, 0.5]
...
>>> def bounds_x(y):
... return [0, 1-2*y]
...
>>> integrate.nquad(f, [bounds_x, bounds_y])
(0.010416666666666668, 4.101620128472366e-16)
结果和上面求出的是一样的。
高斯正交
scipy.integrate还提供了一些功能,以便在固定间隔内进行简单的高斯求积。第一个是fixed_quad,它执行固定阶数的高斯正交。第二个函数是 quadrature,它执行多个阶的高斯正交,直到积分估计值的差低于用户提供的某个容差为止。这些函数都使用模块scipy.special.orthogonal,该模块 可以计算各种正交多项式的根和正交权重(多项式本身可以作为返回多项式类实例的特殊函数使用,例如special.legendre)。
Romberg积分
Romberg方法WPR是另一种用于对积分进行数值计算的方法。有关romberg更多详细信息,请参见点击超链接查看。
使用采样数据进行积分
如果采样数据是等距,且可用样本数恰好是对于某个整数k的 2 k + 1 2^k+1 2k+1 ,那么可以使用Romberg 积分(romb)借助可用的样本来获得积分的高精度估计。Romberg积分使用梯形规则,步长为2的幂次方,然后对这些估计执行Richardson外推,以更高的精度近似积分。
在任意间隔的样本的情况下,可以使用以下两个函数trapz与simps。他们分别使用1和2阶的Newton-Coates公式执行积分。梯形法(trapz)则将函数近似为相邻点之间的直线,而辛普森法(simps)则将函数近似为三个相邻点之间的抛物线。
如果函数是3阶或更少阶的多项式,则对于奇数均等间隔的样本,Simpson规则是精确的。如果样本的间距不相等,则仅当函数为2阶或更小的多项式时,结果才是精确的。使用方法如下:
>>> import numpy as np
>>> def f1(x):
... return x**2
...
>>> def f2(x):
... return x**3
...
>>> x = np.array([1,3,4])
>>> y1 = f1(x)
>>> from scipy.integrate import simps
>>> I1 = simps(y1, x)
>>> print(I1)
21.0
>>> y2 = f2(x)
>>> I2 = integrate.simps(y2, x)
>>> print(I2)
61.5
而:

因此数值解与精确解不对应。盖因f2中多项式的阶数大于2。
使用低级回调函数加快积分<未翻译>
希望减少的积分时间用户可以通过传递一个C函数指针scipy.LowLevelCallable到quad,dblquad, tplquad或nquad和其将被集成并在Python返回结果。
这里的性能提高来自两个因素。主要的改进是更快的函数求值,这是由函数本身的编译提供的。此外,通过删除中的C和Python之间的函数互相调用,我们可以提高速度 quad。对于诸如正弦之类的函数,此方法可以提供约2倍的速度改进;但对于更复杂的功能,可以产生更明显的改进(10x +)。
此功能面向具有大量数字积分的用户,他们愿意写一点C来显着减少计算时间。
例如,可以通过ctypes几个简单的步骤使用该方法:
1.)用函数签名在C中编写一个被积分函数 ,其中x是一个数组,其中包含函数f的求值点,以及 要提供的任意其他数据。double f(int n, double *x, void *user_data)xuser_data
/* testlib.c */
double f(int n, double *x, void *user_data) {
double c = *(double )user_data;
return c + x[0] - x[1] * x[2]; / corresponds to c + x - y * z */
}
2.)现在将此文件编译到共享/动态库中(由于它依赖于OS,因此快速搜索将对此有所帮助)。用户必须链接使用的所有数学库等。在linux上,它看起来像:
$ gcc -shared -fPIC -o testlib.so testlib.c
输出库将称为testlib.so,但它可能具有不同的文件扩展名。现在已经创建了一个库,可以使用将该库加载到Python中ctypes。
3.)负载使用共享库成Python ctypes和集restypes和 argtypes-这允许SciPy的正确解释的功能:
import os, ctypes
from scipy import integrate, LowLevelCallable
lib = ctypes.CDLL(os.path.abspath('testlib.so'))
lib.f.restype = ctypes.c_double
lib.f.argtypes = (ctypes.c_int, ctypes.POINTER(ctypes.c_double), ctypes.c_void_p)
c = ctypes.c_double(1.0)
user_data = ctypes.cast(ctypes.pointer(c), ctypes.c_void_p)
func = LowLevelCallable(lib.f, user_data)
函数的最后一个是可选的,如果不需要,可以省略(在C函数和ctypes argtypes中)。请注意,坐标以双精度数组而不是单独的参数传递。void *user_data
4.)现在像往常一样调用积分函数,在这里使用nquad:
>>> integrate.nquad(func, [[0, 10], [-10, 0], [-1, 1]])
(1200.0, 1.1102230246251565e-11)
Python元组在明显更少的时间内按我们的预期返回。所有可选参数都可以与此方法一起使用,包括指定奇异性,无限边界等。
常微分方程(solve_ivp)
给定初始条件,对一组常微分方程(ODE)进行积分是另一个有用的示例。该函数 solve_ivp在SciPy中可用,用于积分一阶矢量微分方程:

给定初始条件
y = y 0 =y_0 =y0,其中y是一个长度为N的向量,而f是一个从 R N R^N RN到 R N R^N RN上的映射。通过将中间导数引入到方程中,可以始终将高阶常微分方程简化为此类微分方程。
例如,假设希望找到以下二阶微分方程的解:

有初始条件 和 已知具有这些边界条件的微分方程的解是Airy函数
这提供了一种使用来检查积分器的方法special.airy。
首先,通过设置将该ODE转换为标准格式 和 。因此,微分方程变为
换一种说法,
作为一个有趣的提醒,如果 通勤 在矩阵相乘下,则该线性微分方程使用矩阵指数具有精确解:
但是,在这种情况下, 并且其积分不上下班。
这个微分方程可以使用函数solve_ivp进行求解。它需要导数fprime,时间跨度[t_start,t_end] 和初始条件向量y0作为输入参数,并返回一个对象,该对象的y字段是一个具有连续解值的数组作为列。因此,初始条件在输出的第一列中给出。
>>> from scipy.integrate import solve_ivp
>>> from scipy.special import gamma, airy
>>> y1_0 = +1 / 3**(2/3) / gamma(2/3)
>>> y0_0 = -1 / 3**(1/3) / gamma(1/3)
>>> y0 = [y0_0, y1_0]
>>> def func(t, y):
... return [t*y[1],y[0]]
...
>>> t_span = [0, 4]
>>> sol1 = solve_ivp(func, t_span, y0)
>>> print("sol1.t: {}".format(sol1.t))
sol1.t: [0. 0.10097672 1.04643602 1.91060117 2.49872472 3.08684827
3.62692846 4. ]
可以看出,solve_ivp如果没有另外指定,则自动确定其时间步长。为了solve_ivp与airy 函数的解进行比较,将创建的时间向量solve_ivp传递给airy函数。
>>>
>>> print("sol1.y[1]: {}".format(sol1.y[1]))
sol1.y[1]: [0.35502805 0.328952 0.12801343 0.04008508 0.01601291 0.00623879
0.00356316 0.00405982]
>>> print("airy(sol.t)[0]: {}".format(airy(sol1.t)[0]))
airy(sol.t)[0]: [0.35502805 0.328952 0.12804768 0.03995804 0.01575943 0.00562799
0.00201689 0.00095156]
solve_ivp使用标准的参数求出的解与airy函数的差异非常大。为了尽可能的减小这个差异,可以使用相对和绝对的容差。
<相对容差就是“ relative tolerances”,绝对误差是“absolute tolerances”,分别是下文定义的rtol和atol,译者注>
>>> rtol, atol = (1e-8, 1e-8)
>>> sol2 = solve_ivp(func, t_span, y0, rtol=rtol, atol=atol)
>>> print("sol2.y[1][::6]: {}".format(sol2.y[1][0::6]))
sol2.y[1][::6]: [0.35502805 0.19145234 0.06368989 0.0205917 0.00554734 0.00106409]
>>> print("airy(sol2.t)[0][::6]: {}".format(airy(sol2.t)[0][::6]))
airy(sol2.t)[0][::6]: [0.35502805 0.19145234 0.06368989 0.0205917 0.00554733 0.00106406]
若要明确指定用户自定义的时间点对于solve_ivp,solve_ivp 提供了两种可互补使用的方案。通过将t_eval 这个可选参数传递给函数solve_ivp,可在输出中返回t_eval这些时间点的解。
>>> import numpy as np
>>> t = np.linspace(0, 4, 100)
>>> sol3 = solve_ivp(func, t_span, y0, t_eval=t)
如果已知函数的雅可比矩阵,则可以将其传递给以solve_ivp 获得更好的结果。但是请注意,默认积分方法 RK45不支持jacobian矩阵,因此必须选择另一种积分方法。支持雅可比矩阵的集成方法之一是例如Radau以下示例的方法。
>>>
>>> def gradient(t, y):
... return [[0,t], [1,0]]
>>> sol4 = solve_ivp(func, t_span, y0, method='Radau', jac=gradient)
用带状雅可比矩阵求解系统<未翻译完>
<译者注:这一段前面知识铺垫内容讲得比较多,主要涉及的是用带状雅克比矩阵进行加速求解的内容,而与前面的理论铺垫无关。因此可以直接跳到后面看加速效果。>
odeint支持带状的雅可比矩阵。对于已知为刚性的大型微分方程组,这可以显着提高性能。
例如,我们将使用线[MOL]的方法求解一维Gray-Scott偏微分方程。Gray-Scott方程包含v(x,t)和u(x,t),在区间[0,L] 上面有以下两个式子:
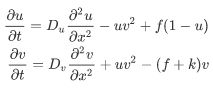
其中,组件的扩散系数 D u D_u Du和 D v D_v Dv ,以及f和k都是常数。(有关该系统的更多信息,请参见 http://groups.csail.mit.edu/mac/projects/amorphous/GrayScott/)
我们假设Neumann(即“无通量”)边界条件:

为了应用线法,我们通过定义宽度为N的等距网格来离散化x,其中 x 0 = 0 , x N = L x_0=0,x_N=L x0=0,xN=L。
以及:
![]()
并且将x的导数替换为有限的变量。通过定义的等距网格来变量 点数 ,带有 和 。我们定义 和 ,然后替换 具有有限差异的导数。那是,
然后我们有一个系统 常微分方程:
(1)
为方便起见, 论点已被删除。
为了强制执行边界条件,我们引入了“鬼影”点 和 ,并定义 , ; 和 类似地定义。
然后
(2)
和
(3)
我们完整的系统 常微分方程是(1) 用于,以及(2)和(3)。
现在,我们可以开始在代码中实现此系统。我们必须结合起来 和 成为长度的单个向量 。两个明显的选择是 和 。从数学上来说,这并不重要,但是选择会影响odeint解决系统的效率。原因在于顺序如何影响雅可比矩阵的非零元素的模式。
当变量按如下顺序排列时 ,雅可比矩阵的非零元素的模式为
变量交错的雅可比模式为 是
在这两种情况下,只有五个平凡的对角线,但是当变量交错时,带宽要小得多。也就是说,主对角线和紧接在主对角线上方的两个对角线以及紧接在主对角线下方的两个对角线是非零对角线。这是重要的,因为输入mu和ml 的odeint是雅可比矩阵的上部和下部的带宽。当变量是交错的, mu并且ml是2,当变量堆叠 以下 ,上限和下限带宽是 。
做出决定后,我们可以编写实现微分方程组的函数。
首先,我们定义系统的来源和反应项的功能:
def G(u, v, f, k):
return f * (1 - u) - u*v**2
def H(u, v, f, k):
return -(f + k) * v + u*v**2
接下来,我们定义计算微分方程组右侧的函数:
def grayscott1d(y, t, f, k, Du, Dv, dx):
“”"
Differential equations for the 1-D Gray-Scott equations.
The ODEs are derived using the method of lines.
"""
# The vectors u and v are interleaved in y. We define
# views of u and v by slicing y.
u = y[::2]
v = y[1::2]
# dydt is the return value of this function.
dydt = np.empty_like(y)
# Just like u and v are views of the interleaved vectors
# in y, dudt and dvdt are views of the interleaved output
# vectors in dydt.
dudt = dydt[::2]
dvdt = dydt[1::2]
# Compute du/dt and dv/dt. The end points and the interior points
# are handled separately.
dudt[0] = G(u[0], v[0], f, k) + Du * (-2.0*u[0] + 2.0*u[1]) / dx**2
dudt[1:-1] = G(u[1:-1], v[1:-1], f, k) + Du * np.diff(u,2) / dx**2
dudt[-1] = G(u[-1], v[-1], f, k) + Du * (- 2.0*u[-1] + 2.0*u[-2]) / dx**2
dvdt[0] = H(u[0], v[0], f, k) + Dv * (-2.0*v[0] + 2.0*v[1]) / dx**2
dvdt[1:-1] = H(u[1:-1], v[1:-1], f, k) + Dv * np.diff(v,2) / dx**2
dvdt[-1] = H(u[-1], v[-1], f, k) + Dv * (-2.0*v[-1] + 2.0*v[-2]) / dx**2
return dydt
我们不会实现一个计算雅odeint可比矩阵的函数,但是我们会告诉我们 雅可比矩阵是带状的。这允许基础求解器(LSODA)避免计算它知道为零的值。对于大型系统,这将显着提高性能,如以下ipython会话所示。
首先,我们定义所需的输入:
In [31]: y0 = np.random.randn(5000)
In [32]: t = np.linspace(0, 50, 11)
In [33]: f = 0.024
In [34]: k = 0.055
In [35]: Du = 0.01
In [36]: Dv = 0.005
In [37]: dx = 0.025
在不利用雅可比矩阵的带状结构的情况下计时计算时间:
In [38]: %timeit sola = odeint(grayscott1d, y0, t, args=(f, k, Du, Dv, dx))
1 loop, best of 3: 25.2 s per loop
现在设置ml=2和mu=2,因此odeint知道雅可比矩阵是带状的:
In [39]: %timeit solb = odeint(grayscott1d, y0, t, args=(f, k, Du, Dv, dx), ml=2, mu=2)
10 loops, best of 3: 191 ms per loop
那快很多!
让我们确保他们计算出相同的结果:
In [41]: np.allclose(sola, solb)
Out[41]: True
