数字图像处理 第四章 频率域滤波

一、单变量的傅里叶变换（DFT）

1.1DFT及其反变换IDFT

其中$W_N=e^{-j\frac{2\pi }{N}}$。

1.2DFT的重要性质

1.2.1奇偶对称性

1.2.2虚实特性

1.2.3复序列性质

1.3采样定理

1.3.1不失真采样条件

1.3.2采样的恢复

    可以分析出，DFT点数越多，则用它恢复模拟频谱就会越精确。通过以下两种方法可以增加DFT点数N。
    （1）提高采样频率$f_s$。
    （2）增大序列长度（充0）。

二、两个变量的函数的扩展

2.1二维连续傅里叶变换对

傅里叶变换：$$F(u,v)={\int }_{-\propto }^{+\propto }{\int }_{-\propto }^{+\propto }f(t,z)e^{-j2\pi (ut+vz)}dtdz$$
傅里叶反变换：$$f(t,z)={\int }_{-\propto }^{+\propto }{\int }_{-\propto }^{+\propto }F(u,v)e^{j2\pi (ut+vz)}dudv$$

2.2二维傅里叶变换的性质

2.2.1平移与旋转

$f(x,y)e^{j2\pi (u_{0}x/M=v_{0}y/N)}\iff F(u-u_0,v-v_0)$
$f(x-x_0,y-y_0)\iff F(u,v)e^{-j2\pi (x_{0}u/M+y_{0}v/N)}$

2.2.2周期性

$F(u,v)=F(u+k_{1}M,v)=F(u,v+k_{2}N)=F(u+k_{1}M,v+k_{2}N)$
$f(x,y)=f(x+k_{1}M,y)=f(x,y+k_{2}N)=f(x+k_{1}M,y+k_{2}N)$

2.2.3对称性

偶数部分：$W_e(x,y)=\frac{w(x,y)+w(-x,-y)}{2}$
奇数部分：$W_o(x,y)=\frac{w(x,y)-w(-x,-y)}{2}$

2.3Python实现傅里叶变换

import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('demo.jpg', 0)
rows, cols = img.shape
print(rows, cols)
# 计算DFT效率最佳的尺寸
nrows = cv2.getOptimalDFTSize(rows)
ncols = cv2.getOptimalDFTSize(cols)
print(nrows, ncols)
nimg = np.zeros((nrows, ncols))
nimg[:rows, :cols] = img
img = nimg
# OpenCV计算快速傅里叶变换，输入图像应首先转换为np.float32，然后使用函数cv2.dft()和cv2.idft()。
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)
magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))
plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()
rows, cols = img.shape
crow, ccol = rows // 2, cols // 2
# 首先创建一个mask，中心正方形为1，其他均为0
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 1
# 应用掩码Mask和求IDTF
fshift = dft_shift * mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:, :, 0], img_back[:, :, 1])
plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(img_back, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

三、 频率域滤波基础

3.1频率域的滤波

    和F的相乘在逐元素的基础上定义，即H的 第一个元素乘以F的第一个元素，H的第二个元素乘以F的第二个元素。一般，F的元素为复数，H的元素为实数。H为零相移滤波器，因为滤波器不改变变换的相位，F中实部和虚部的乘数(H)可以抵消相角$\varphi (u,v)=arctan\frac{I(u,v)}{R(u,v)}$。

3.2频率域的滤波步骤

    （1）用$(-1{)}^{x+y}$乘以输入图像进行中心变换$f(x,y)(-1{)}^{{}^{x+y}}\iff F(u-M/2,v-N/2)$；
    （2）计算（1）中的DFT F(u,v)；
    （3）用滤波器函数H(u,v)乘以F(u,v)；
    （4）计算（3）中结果的IDFT；
    （5）得到4中结果的实部；
    （6）用$(-1{)}^{x+y}$乘以（5）中的结果，取消输入图像的乘数。

3.3空间和频率域滤波间的对应

    空间域和频率域滤波间的纽带是卷积定理。
$h(x,y)\iff H(u,v)$，$h(x,y)$是一个空间滤波器，$H(u,v)$称为的脉冲响应。
    公式表明，空间域和频率域中的滤波器组成了傅 里叶变换对。给出在频率域的滤波器，可以通过反傅里叶变换得到 在空间域对应的滤波器，反之亦然。滤波在频率域中更为直观，但在空间域一般使用更小 的滤波器模板。可以在频率域指定滤波器，做反变换，然后在空间域 使用结果滤波器作为在空间域构建小滤波器模板的指导。对应关系如下图所示。

    结论：
    （1）低通滤波器： 当H(u)有很宽的轮廓时(大的$\sigma$值)，h(x)有 很窄的轮廓，反之亦然。当接近无限时， H(u)趋于常量函数，而h(x)趋于冲激函数。两个低通滤波器的相似之处在于两个域中的 值均为正。所以，在空间域使用带正系数的模板可以实现低通滤波。频率域低通滤波器越窄，滤除的低频成分就越多，使得图像就越模糊；在空间域，这意味着低通滤波器就越宽，模板就越大。
    （2）高通滤波器：空间域滤波器有正值和负值，一旦值变为负数，就再也不会变为正数。为什么频率域中的内容在空间域要使用小空间模板。频率域可以凭直观指定滤波器，空间域滤波效果取决于空间模板的大小。

四、使用频率域滤波器平滑图像

4.1理想低通滤波器

    截断傅里叶变换中的所有高频成分，这些高 频成分处于指定距离之外
$H(u,v)=\{\begin{array}{ccc}1& D(u,v)\le D_0& \\ 0& D(u,v)>D_0& \end{array}$
    频率矩形的中心在(u,v)=(M/2,N/2),从点(u,v)到中心的距离如下：
$D(u,v)=[(u-P/2{)}^2+(v-Q/2{)}^2{]}^{1/2}$

    上图说明在半径为的圆内，所有频率没有衰减地通过滤波器，而在此半径的圆之外的所有频率完全被衰减掉。
理想低通滤波器距离——具有振铃现象，如下图所示。

4.2布特沃斯低通滤波器

    n级巴特沃斯低通滤波器（BLPF）定义如下：
$$H(u,v)=\frac{1}{1+[D(u,v)/D_0{]}^{2n}}$$
    $D_{{}_0}$为截至频率距原点的距离，D(u,v)是点(u,v)距原点的距离。不同于ILPF，BLPF变换函数在通带与被滤除的频率之间没有明显的截断.当D(u,v)=D0时，H(u,v)=0.5(最大值是1，当 D(u,v)=0)

    进行平滑以改进图像质量。通常，BLPF的平滑效果好于ILPF（振铃现象）。
布特沃斯低通滤波器n=2时的结果如下图。

4.3高斯低通滤波器

     二维高斯低通滤波器（GLPF）定义如下：
$H(u,v)=e^{-D^2(u,v)/2{\sigma }^2}$，D(u,v)是点(u,v)距原点的距离，使
$\sigma =D_{{}_0}$。
$H(u,v)=e^{-D^2(u,v)/2D_0^2}$，当D(u,v)=时，滤波器下降到它最大值的0.607处。
    使用高斯低通滤波器平滑图像结果如下图所示：

    结论：GLPF不能达到有相同截止频率的二阶 BLPF的平滑效果，GLPF没有振铃。如果需要严格控制低频和高频之间截至频率的过渡，选用BLPF，代价是可能 产生振铃。

五、使用频率域滤波器锐化图像

5.1理想高通滤波器

    截断傅里叶变换中的所有低频成分，这些低 频成分处于指定距离$D_0$之内，
$H(u,v)=\{\begin{array}{ccc}0& D(u,v)\le D_0& \\ 1& D(u,v)>D_0& \end{array}$
    频率矩形的中心在(u,v)=(M/2,N/2)，从点 (u,v)到中心（原点）的距离如下：
$D(u,v)=[(u-M/2{)}^2+(v-N/2{)}^2{]}^{1/2}$
    使用IHPF对图像滤波后的结果如下图：

结论：图a和图b的振铃问题十分明显。

5.2布特沃斯高通滤波器

    n阶且截至频率距原点的距离为$D_0$的巴特沃 思高通滤波器(BHPF)定义为:
$H(u,v)=\frac{1}{1+[D_0/D(u,v){]}^{2n}}$
    二阶布特沃斯高通滤波器对图像滤波的结果如下图所示：

     结论：BHPF的结果比IHPF的结果平滑得多。

5.3高斯高通滤波器

    截频距原点为$D_0$的高斯高通滤波器(GHPF)定义为:
$H(u,v)=1-e^{-D^2(u,v)/2D_0^2}$
$D(u,v)=[(u-M/2{)}^2+(v-N/2{)}^2{]}^{1/2}$
    高斯高通滤波器对图像滤波的结果如下图所示：

5.4频率域的拉普拉斯算子

    原点从(0,0)移到(M/2,N/2),所以，滤波函数平移为$H(u,v)=-[(u-M/2{)}^2+(v-N/2{)}^2]$，空间域拉普拉斯算子过滤后的图像可由计算 H(u,v)F(u,v)的反傅里叶变换得到${▽}^{2}f(x,y)={\Im }^{-1}\left\{-[(u-M/2{)}^2+(v-N/2{)}^2]F(u,v)\right\}$。
    使用拉普拉斯算子在频率域锐化图像的结果如下图所示：

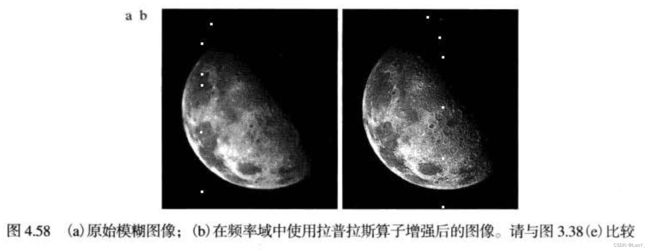
5.5钝化模板、高频提升滤波和高频加强滤波

    钝化模板(锐化或高通图像)：从一幅图像减去 其自身模糊图像而生成的锐化图像构成。在频率 域，即从图像本身减去低通滤波（模糊）后的图 像而得到高通滤波（锐化）的图像：
$f_{hp}(x,y)=f(x,y)-f_{lp}(x,y)$。
    高频提升过滤：$f_{hp}(x,y)=Af(x,y)-f_{lp}(x,y)$，当A=1，即高通过滤；当A＞1，累加图像本身。由$H_{hp}(u,v)=1-H_{lp}(u,v)$，高频提升过滤可以定义为$H_{hp}(u,v)=(A-1)+H_{hp}(u,v)$。
高频提升加强：$H_{hp}(u,v)=a+b{H}_{lp}(u,v)$，$a\ge 0$，$b>a$。用图像的高频成分进行增强，增加a的目的是使零频率不被滤波器过滤。当a=A-1,b=1时转化为高频提升过滤；当b>1，高频得到加强。
    高频提升加强示例如下图所示：

六、总结

    频率就是变化的快慢，傅里叶变换把图像从空域变换到频域。在频域中，高频分量表示图像灰度变换比较快的地方，比如物体的边缘。而物体内部比较平坦的区域，灰度基本没有变化或变化较小，对应的就是低平分量。
    由于图像中的噪声主要集中在图像的高频部分，为了去除噪声，改善图像质量，可以采用低通滤波器来抑制高频部分，然后再进行傅里叶反变换获得滤波图像，可以达到图像平滑的目的，常用的频率域低通滤波器有理想低通滤波器、布特沃斯低通滤波器和高斯低通滤波器。这三种滤波器中理想滤波器平滑效果最好，但是高斯滤波器中没有振铃现象。通过对低通滤波器的反操作，可以得到高通滤波器。
    通过本章的学习，巩固了傅里叶变换的知识，同时也开始尝试使用Python去实现这些算法，理解有些不熟练，还是得多实践。

​