SVM学习
目录
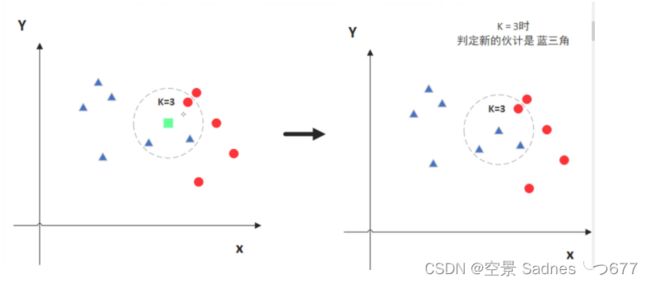
SVM和KNN的对比分析。
SVM原理梳理
支持向量积：
寻找支持向量：
SVM代码在百度飞桨（鸢尾花）
加载相关包
加载数据、切分数据集
构建SVM分类器，训练函数
初始化分类器实例，训练模型
展示训练结果及验证结果
实验结果
SVM和KNN的对比分析。
信息内容借用来源：
(38条消息) [cs231n]KNN与SVM区别_Rookie’Program的博客-CSDN博客
| KNN | SVM |
| 没有训练过程，只是将训练数据与训练数据进行距离度量来实现分类。基本原理就是找到训练数据集里面离需要预测的样本点距离最近的k个值（距离可以使用比如欧式距离，k的值需要自己调参），然后把这k个点的label做个投票，选出一个label做为预测 | 是先在训练集上训练一个模型，然后用这个模型直接对测试集进行分类。这两个步骤是独立的。 需要超平面wx+b来分割数据集（此处以线性可分为例），因此会有一个模型训练过程来找到w和b的值。训练完成之后就可以拿去预测了，根据函数y=wx+b的值来确定样本点x的label，不需要再考虑训练集 |
| knn没有训练过程，但是预测过程需要挨个计算每个训练样本和测试样本的距离，当训练集和测试集很大时，预测效率低。 | svm有一个训练过程，训练完直接得到超平面函数，根据超平面函数直接判定预测点的label，预测效率很高 |
| 物以类聚，人以群分。如果你的朋友里大部分是北京人，就预测你也是北京人。如果你的朋友里大部分是河北人，那就预测你是河北人。不管你住哪里。 | 就像是在河北和北京之间有一条边界线，如果一个人居住在北京一侧就预测为北京人，在河北一侧，就预测为河北人。但是住在河北的北京人和住在北京的河北人就会被误判。 |
| KNN对每个样本都要考虑。 | SVM是要去找一个函数把达到样本可分 |
| KNN不能处理样本维度太高的东西 | SVM处理高纬度数据比较优秀 |
| 假设每条数据有两个特征值x和y，一个label，即点的颜色，先将所有数据放在平面直角坐标系中，如下图1.1的红点和蓝点，红点和蓝点所构成的所有点即为训练集，而绿点则是测试点，k最邻近问题的最邻近就是直观的邻近的意思，即离得近，而k指的是找几个离得最近的，如果k=3，那么所选的点即为实线所包含的三个点，若k=5，则为虚线所包含的五个点，而对于预测点分类的预测则是根据所选k个点中最多个数的类别所确定，同样以下图为例，如果k=3，那么预测点的结果将为红色（2个红色，1个蓝色），如果k=5，那么预测点的结果将为蓝色（3个蓝色，2个红色），由此可见，参数k的选取直接影响了预测结果的准确度。 |
SVM 指的是这个模型是一个机器，此外它的作用是分类，所以可以理解为一个分类用的机器，support vevtoe之后再介绍。同样为了简单介绍采用二维介绍，样本同样是带有颜色label的有x和y两个属性的训练点集合，svm要要找一条线，使得把两个类别的点区分开来，那么对于接下来的测试点，看测试点位于哪一侧，就将其归类于该类，那么问题来了，符合这个要求的线有很多条，比如图中的黑线和灰线就是其中的两条，那么什么才是最优解呢，现在就要介绍support vector了，就是两个类别中的点离这条分割线最近的距离，如何才是最优解呢，就是让两个类别的离分割线最近的点，再回到最近的问题，什么才是最优解呢，那就是支持向量离分割线越远越好，因为距离越远，允许容纳的点越多，使得分类的越平均，更加理想。 |
 |
 |
| 选择KNN的场景 | 选择SVM的场景 |
| 准确度不需要精益求精。 |
需要提高正确率。 |
| 样本不多。 | 样本比较多。 |
| 样本不能一次性获取。智能随着时间一个个得到 | 样本固定，并且不会随着时间变化。 |
SVM原理梳理
支持向量积：
1> 两个范围区域中哪两个点相对来说比较近（挑出来作为支持向量）
2>找出一条决策边界将其分开
注意：支持向量要较小的，考虑离自己最近的雷
决策边界要大的，要最宽的道路才能行动的更快，不容易踩雷
寻找支持向量：
距离与数据定义：在平面上构造了直线，点到平面的距离公式，借助了向量和法向量进行相关求解
具体步骤：
1. 距离计算（点到平面距离）
点知道，面不知道（面为假设），用到向量和法向量知识
2. 目标函数
目的：找到一条线，使得离该线最近的点最远
放缩变换和优化目标
目标函数能够体现SVM的基本定义
3. 部分数学原理
拉格朗日乘子法（约束条件下求极值）
求偏导，为了求极值
简化最终目标函数
4.软间隔优化
考虑一些异常的噪音，让分类更合理。（引入松弛因子）
目标函数的变化，及C的引入（能够体现容错能力）
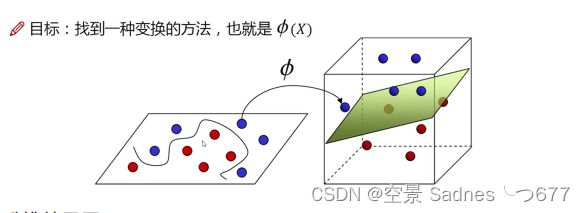
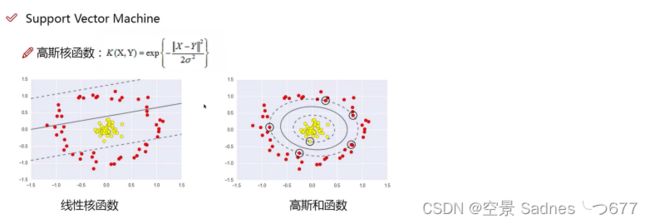
5. 核函数 （分类好的关键）
升维，二位的变成三维的，可能能够很好的用平面分开
升维效果展示
映射到高维，可能更好看出来不同，但确实计算量增大了很多 
高斯核函数
SVM代码在百度飞桨（鸢尾花）
加载相关包
import numpy as np #数据转换
from matplotlib import colors #作图有关包
from sklearn import svm #sklearn工具包
from sklearn import model_selection #sklearn工具包
import matplotlib.pyplot as plt #作图有关包
import matplotlib as mpl #作图有关包加载数据、切分数据集
# ======将字符串转化为整形==============
def iris_type(s):
it = {b'Iris-setosa':0, b'Iris-versicolor':1,b'Iris-virginica':2}
return it[s] #转换鸢尾花的名字为0，1，2
# 1 数据准备
# 1.1 加载数据
data = np.loadtxt('/home/aistudio/data/data2301/iris.data', # 数据文件路径i
dtype=float, # 数据类型
delimiter=',', # 数据分割符
converters={4:iris_type}) # 将第五列使用函数iris_type进行转换
# 1.2 数据分割
x, y = np.split(data, (4, ), axis=1) # 数据分组 第五列开始往后为y 代表纵向分割按列分割
x = x[:, :2] #纵向分割，讲后两列分割
x_train, x_test, y_train, y_test=model_selection.train_test_split(x, y, random_state=1, test_size=0.2)
#random_state，控制随机状态,固定random_state后，每次构建的模型是相同的、生成的数据集是相同的、每次的拆分结果也是相同的
# x_train:包括所有自变量,这些变量将用于训练模型
#同样，我们已经指定测试_size=0.2，这意味着来自完整数据的80%的观察值将用于训练/拟合模型，其余2O%将用于测试模型
# y_train-这是因变量，需要此模型进行预测，其中包括针对自变量的类别标签，我们需要在训练/拟合模型时指定我们的因变量
#x_test:这是数据中剩余的20%的自变量部分，这些自变量将不会在训练阶段使用，并将用于进行预测，以测试模型的准确性。
# y _test-此数据具有测试数据的类别标签，这些标签将用于测试实际类别和预测类别之间的准确性。
构建SVM分类器，训练函数
# SVM分类器构建
def classifier():
###############################################
###############################################
############# 在此处添加代码 ############
###############################################
###############################################
return clf
# 训练模型
def train(clf, x_train, y_train):
###############################################
###############################################
############# 在此处添加代码 ############
###############################################
###############################################
初始化分类器实例，训练模型
# 2 定义模型 SVM模型定义
clf = classifier()
# 3 训练模型
train(clf, x_train, y_train)展示训练结果及验证结果
# ======判断a,b是否相等计算acc的均值
def show_accuracy(a, b, tip):
acc = a.ravel() == b.ravel()
print('%s Accuracy:%.3f' %(tip, np.mean(acc)))
# 分别打印训练集和测试集的准确率 score(x_train, y_train)表示输出 x_train,y_train在模型上的准确率
def print_accuracy(clf, x_train, y_train, x_test, y_test):
print('training prediction:%.3f' %(clf.score(x_train, y_train)))
print('test data prediction:%.3f' %(clf.score(x_test, y_test)))
# 原始结果和预测结果进行对比 predict() 表示对x_train样本进行预测,返回样本类别
show_accuracy(clf.predict(x_train), y_train, 'traing data')
show_accuracy(clf.predict(x_test), y_test, 'testing data')
# 计算决策函数的值 表示x到各个分割平面的距离
print('decision_function:\n', clf.decision_function(x_train))
def draw(clf, x):
iris_feature = 'sepal length', 'sepal width', 'petal length', 'petal width'
# 开始画图
x1_min, x1_max = x[:, 0].min(), x[:, 0].max()
x2_min, x2_max = x[:, 1].min(), x[:, 1].max()
# 生成网格采样点
x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]
# 测试点
grid_test = np.stack((x1.flat, x2.flat), axis = 1)
print('grid_test:\n', grid_test)
# 输出样本到决策面的距离
z = clf.decision_function(grid_test)
print('the distance to decision plane:\n', z)
grid_hat = clf.predict(grid_test)
# 预测分类值 得到[0, 0, ..., 2, 2]
print('grid_hat:\n', grid_hat)
# 使得grid_hat 和 x1 形状一致
grid_hat = grid_hat.reshape(x1.shape)
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'b', 'r'])
plt.pcolormesh(x1, x2, grid_hat, cmap = cm_light)
plt.scatter(x[:, 0], x[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark )
plt.scatter(x_test[:, 0], x_test[:, 1], s=120, facecolor='none', zorder=10 )
plt.xlabel(iris_feature[0], fontsize=20) # 注意单词的拼写label
plt.ylabel(iris_feature[1], fontsize=20)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
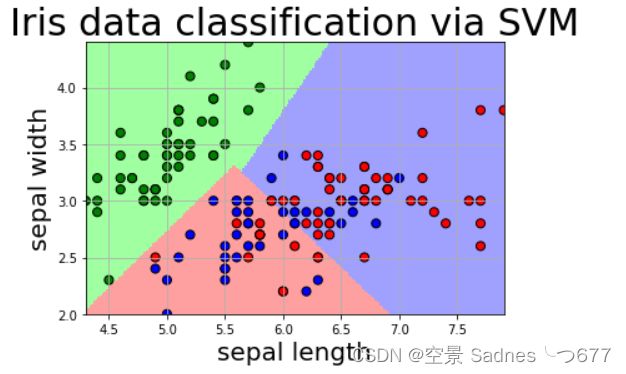
plt.title('Iris data classification via SVM', fontsize=30)
plt.grid()
plt.show()
# 4 模型评估
print('-------- eval ----------')
print_accuracy(clf, x_train, y_train, x_test, y_test)
# 5 模型使用
print('-------- show ----------')
draw(clf, x) 实验结果
-------- eval ----------
training prediction:0.808
test data prediction:0.767
traing data Accuracy:0.808
testing data Accuracy:0.767
decision_function:
[[-0.24991711 1.2042151 2.19527349]
[-0.30144975 1.25525744 2.28694265]
[-0.24281146 2.24318221 0.99502737]
[-0.27672959 1.2395788 2.23333857]
[-0.23718563 2.21927504 1.11750062]
[ 2.24124823 -0.20327106 0.82871773]
[-0.24916991 2.25488962 0.92530871]
[ 2.2222485 0.86479883 -0.18955173]
[-0.28036071 1.24228023 2.24154874]
[-0.29229603 1.26471537 2.25517554]
[-0.28446963 1.23293167 2.25928719]
[ 2.24433312 0.82415773 -0.20653214]
[-0.28058919 2.2680431 1.18280403]
[-0.2685366 1.22653818 2.22306948]
[-0.28088362 1.23636902 2.24824728]
[-0.3051288 1.27363886 2.28725744]
[ 2.19125377 -0.19835874 1.03664074]
[ 2.25909278 0.7973515 -0.21992546]
[ 2.23082124 1.05792561 -0.23704919]
[ 0.9071986 2.20602139 -0.18401877]
[ 2.23542016 0.85310906 -0.20593739]
[ 2.17688585 -0.13662868 0.89878446]
[-0.2901959 1.13009006 2.28629999]
[-0.2849149 1.2256961 2.26370915]
[-0.29702633 1.25351358 2.277823 ]
[-0.27672959 1.2395788 2.23333857]
[-0.26773664 1.23366473 2.21155174]
[-0.18376448 1.04634559 2.17207981]
[-0.3034019 1.26567438 2.28710058]
[-0.19335707 2.1789894 1.06048442]
[ 2.26111102 0.82507149 -0.23839539]
[-0.25175432 2.24568274 1.07353366]
[-0.27612009 1.24511631 2.22395753]
[ 2.23082124 1.05792561 -0.23704919]
[ 2.2564785 0.88137735 -0.24525952]
[-0.27392297 1.22235345 2.24092419]
[ 2.27186349 0.81063773 -0.25217964]
[-0.24991711 1.2042151 2.19527349]
[-0.26570402 1.19126129 2.24029108]
[-0.27848257 1.2178274 2.2538024 ]
[-0.22451542 2.21500409 1.06585832]
[-0.27155037 1.18375822 2.2533339 ]
[-0.24054376 1.19871464 2.17582039]
[ 2.26342438 -0.22589317 0.79171647]
[-0.28058919 2.2680431 1.18280403]
[-0.27325118 1.23002938 2.23296907]
[-0.27392297 1.22235345 2.24092419]
[ 0.83829222 2.24377366 -0.21341635]
[-0.24516302 1.14882472 2.2212494 ]
[-0.23166652 2.24053482 0.92047491]
[ 2.22969047 -0.19768814 0.85619186]
[ 2.22880454 0.99577113 -0.22838164]
[ 2.27145869 -0.24964429 0.80531071]
[-0.27155037 1.18375822 2.2533339 ]
[ 2.26483527 0.94178326 -0.26172128]
[-0.26110752 2.23705292 1.1785139 ]
[-0.27982727 1.24751212 2.23370536]
[-0.22879722 1.19272468 2.14998616]
[ 2.23358198 0.83241849 -0.19030886]
[ 2.22452335 0.89510197 -0.20533704]
[-0.2457942 2.23080526 1.1192022 ]
[ 2.22880454 0.99577113 -0.22838164]
[-0.29975002 1.26103019 2.28055184]
[-0.26301911 1.22280275 2.21100325]
[-0.30016925 1.25327954 2.28493414]
[-0.2813963 1.22963701 2.2540346 ]
[-0.28697192 2.26788659 1.2256914 ]
[-0.22353839 1.09045989 2.20818498]
[-0.28117478 1.14500651 2.27402976]
[-0.18956974 2.19344513 0.97988104]
[ 2.25743255 -0.25828463 1.01583138]
[-0.2457942 2.23080526 1.1192022 ]
[ 2.17277768 1.22898718 -0.25528063]
[-0.24124254 2.24831388 0.92286901]
[-0.2849149 1.2256961 2.26370915]
[ 2.24579933 0.84272184 -0.21897044]
[-0.28890998 1.24952476 2.25968873]
[ 2.25299223 0.81668128 -0.21944995]
[ 2.26111102 0.82507149 -0.23839539]
[-0.23642368 1.10779426 2.22078495]
[-0.20799903 2.21040083 0.9835351 ]
[-0.27904302 1.20814609 2.25888125]
[ 2.23719183 0.87970197 -0.21848687]
[ 2.25804076 0.78683693 -0.20770513]
[-0.20036305 1.13877998 2.14747696]
[ 2.2575743 0.91742515 -0.25144563]
[-0.2457942 2.23080526 1.1192022 ]
[ 2.24054953 0.9647293 -0.23738931]
[-0.27392297 1.22235345 2.24092419]
[ 1.04178458 2.22068685 -0.22589065]
[ 2.26302243 0.86771692 -0.25169177]
[-0.25967114 1.18457321 2.23184401]
[ 2.27008204 0.91974964 -0.26603261]
[-0.16478644 2.17106379 0.9763103 ]
[ 2.25967478 1.03492895 -0.26153197]
[-0.24124254 2.24831388 0.92286901]
[-0.220911 2.26253025 0.78819329]
[ 2.24433312 0.82415773 -0.20653214]
[ 2.21629138 1.08000401 -0.22797453]
[ 0.94499808 2.23194749 -0.22546394]
[ 2.2787295 0.77880195 -0.25266172]
[-0.22879722 1.19272468 2.14998616]
[-0.25647454 1.21879654 2.1959717 ]
[ 2.24579933 0.84272184 -0.21897044]
[-0.27848257 1.2178274 2.2538024 ]
[-0.21088734 2.19937515 1.06319809]
[-0.28656383 2.27063398 1.2147421 ]
[-0.28535213 1.21733665 2.26763273]
[-0.2457942 2.23080526 1.1192022 ]
[ 2.18136055 0.8932065 -0.13975588]
[ 2.19696244 1.09880525 -0.21701131]
[-0.27114143 2.24778105 1.1980246 ]
[-0.26207613 1.23041878 2.19666289]
[-0.29382184 1.2442528 2.27479662]
[-0.24432781 2.23739126 1.07102463]
[-0.27256402 1.23671218 2.2235153 ]
[-0.26483213 1.20360155 2.23222183]
[-0.28211449 2.25818853 1.22483139]
[-0.27848257 1.2178274 2.2538024 ]
[ 2.22880454 0.99577113 -0.22838164]]
-------- show ----------
grid_test:
[[4.3 2. ]
[4.3 2.0120603]
[4.3 2.0241206]
...
[7.9 4.3758794]
[7.9 4.3879397]
[7.9 4.4 ]]
the distance to decision plane:
[[ 1.15418548 2.24935988 -0.26432263]
[ 1.15805875 2.2485129 -0.26434377]
[ 1.16176809 2.24764867 -0.2643649 ]
...
[-0.28260705 0.82993354 2.28954779]
[-0.28228765 0.82682418 2.28953928]
[-0.2819642 0.82383103 2.28953076]]
grid_hat:
[1. 1. 1. ... 2. 2. 2.]
图见下面
