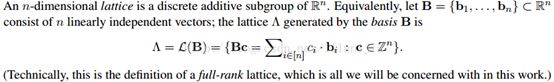(四)格密码-抗量子计算
目录
格密码
格的定义
格密码背景
格问题
格密码发展
格密码特点
LLL算法
LWE(Learning With Errors)
参考推荐:
***格密码学习笔记(一)_中科院大学网安学院五班的博客-CSDN博客_格密码-格、简介、LLL、LWE
格密码学习记录_信息安全学习记录的博客-CSDN博客-预备知识
格密码初步学习记录(二)格的一些数学基础_lllunijia的博客-CSDN博客
基于格密码的算法研究_Mr.Yi的博客-CSDN博客_格加密-LWE、DH
格密码学习记录(二)_信息安全学习记录的博客-CSDN博客-格问题、LLL
格密码开源库PALISADE的使用_周粥粥啊的博客-CSDN博客_格密码库-格密码开源库PALISADE
格密码基础(1)_CCCYYY090的博客-CSDN博客_格密码-格基础
格理论的基础知识_奶油小橙汁儿~的博客-CSDN博客_格理论
格密码
格可以用来阐述一种既不是基于双素数因子分解也不是基于对数问题的公钥密码。
重要概念:
- 格
- 格的基
- 格问题
- 格密码
- 格的行列式:基础区域的面积
- 连续极小:格L中的最短非零向量
- Gram-Schmit正交化(线性代数)
- Minkowski定理
- 可证明安全
- 困难性问题
- LLL算法
- LWE
格的定义
格的概念与向量空间的概念非常相似,就是多了一个限制,即格上只允许格中的向量与整数做标量乘法运算确定球的最大格堆积密度等价于求格的最短向量(SVP)的长度, 确定球的最小格覆盖密度则等价于求到格点的最近距离(CVP)。
格1:
格的定义:任何一组线性无关的向量所生成的系数为整数的向量集合称为格。
这组生成格的线性无关的向量就是格的基,格可以有很多组基,但格的维数是相同的。格的两组基之间可以通过一个行列式为±1的矩阵进行转换。
格2:
欧式空间:是指四维甚至是N维的理论上无穷大的空间
向量空间:向量空间也是一个集合,这个集合对向量的加法和数乘是封闭的,也就是说,只要空间中的运动理解为点到点的移动,而非想象中的连续。向量空间可以理解为所有维度为 n 的实向量的集合。向量在这个空间内,那么向量按照加法和数乘的方式运动,就会一直在这个空间里。Rn则定义为一个维度为n 的实向量空间。
根据向量空间的概念,格的定义如下:
某种程度上,格可以理解成系数为整数的向量空间。
上图为格的几何化表示,其中的点便是格空间中的格点,而两条从原点出发的向量便是这个格空间的一组基向量,可以发现格中所有的格点均可以通过从原点出发的两条向量来进行表示。
格3:
加法群:表示一个拥有满足封闭性、结合律、有单位元、有逆元的加法运算的代数结构G
- 封闭性:即G的任意两个元素在+下的运算结果都是该集合的一个元素
- 结合律:有单位元:e+a=a,a+e=a。在加法群中,e是0
- 有逆:对于任意a属于G,有b属于G,使得a+b=b+a=e;逆元具有唯一性。
一般加法群有 可交换的性质。
加法子群:非空子集H属于G,满足:
对于任意a,b∈H,有a+b∈H,a^-1∈H, a+(b^-1)∈H;
格的定义:
- 格是代数 (L;∧,∨),∧,∨是满足幂等律、交换律、结合律、吸收率的二元运算。
- 格是有序集(L;≤)(有序集:自反性,反对称、传递),对任意x、y∈L,inf{x,y} 和sup{x,y}在L中存在。
扩展到密码学领域:格是Rm空间中具有周期性结构的离散点的集合。来自文献Public-Key Cryptosystems from the Worst-Case Shortest Vector Problem 的定义:
格是一组(n>=m)线性无关向量b1,b2...bn所有整系数的线性无关组合。其中b1,b2...bn称为格的基L(B)。这样一来,L(B)就可以用矩阵来表示。n=m时称为满秩。
例子:以2维的空间举例说明,那么在直角坐标系中,a(1,0),b(0,1)就可以作为L(B)=(a,b),那么构成的格的离散点就为直角坐标系中的所有整数点。这个格显然满足上述的定义。
满足加法群:
- 满足加法子群:格是一组(n>=m)线性无关向量b1,b2...bn所有整系数的线性无关组合,显然满足封闭律
- 结合律:向量(a+b)+c=a+(b+c),满足
有单位元:0向量,满足
- 有逆:对于所有a∈L,有-a∈L,使得a+(-a)=0,成立
a,b∈L,有a+b∈L,a^-1∈L, a+(b^-1)∈L;
满足定义1:
- 设∨为sup,∧为inf,显然成立
满足定义2:
- 自反性:成立
- 反对称:向量a∈L,b∈L,ab=ba,则a=b 成立
- 传递性:向量a,b,c∈L,ab∈L,bc∈L,则ac∈L,成立
格的基并不唯一,格可由不同的基表示。在2维的平面中,除了直角坐标系坐标,还有无数组线性无关的向量可作为格的基。
拓展至m维空间,我们可以抽象理解为一组n维基L(B)所组成的所有整系数坐标点,而这个偏序关系就是向量,这个概念并不准确甚至非常片面,但是能帮助我们在公式推导中有一个简单粗暴的直观的感觉。
其它数学定理:
- 模格(ML) x≤b → x∨(a∧b) = (x∨a)∧b
- 任意链都是模格
- Dedekind判别定理:一个格是模格当且仅当形如N5的子格。
格密码背景
随着当下量子计算机的研制的迅速进展,量子算法亦是相应得以巨大突破。在量子计算模型下,经典数论假设的密码体系(如大整数分解,计算有限域/椭圆曲线上的离散对数问题等),存在多项式时间(PPT)的量子算法,换而言之,经典数论密码体系受到了极大的冲击,将有可能成为旧时代的眼泪。因此,能够抵抗量子计算机攻击的密码——“后量子”或“抗量子”密码便应运而生。
目前, 用于构建后量子密码系统的常见数学技巧包括:
- 杂凑函数,多变量方程(在构造签名方案时较有优势)
- 纠错码(更合适构造加密方案)
- 格(最通用的一类, 几乎所有经典密码概念都可以在格密码中实现)
- 超奇异椭圆曲线同源问题(当下较新的一类, 目前其中较受关注的有密钥交换和签名方案的构造,计算效率很低,还达不到实用性的要求)
量子计算对密码的影响:
| 密码算法 | 量子计算的影响 |
| 对称密码算法(SM4,AES) | 密钥加倍(Grover) |
| 散列函数(SM3,SHA-3) | 输出长度增加(Grover) |
| 经典公钥算法(RSA,DSA,ECC) | 多项式算法(Shor) |
| 格密码 | 未找到有效算法 |
| 多变量密码(数字签名) | 未找到有效算法 |
| 基于Hash的密码(数字签名) | 未找到有效算法 |
| 基于编码的密码(加密) | 未找到有效算法 |
| 超奇异同源 | 未找到有效算法 |
传统公钥密码面临的挑战:
- 安全性挑战:Shor量子分解算法利用量子计算的并行性,对任意大的整数进行快速因子分解,大大降低目前普遍使用的RSA算法的破解时间。随后又出现了针对基于离散对数问题的量子求解算法。这些量子算法的提出意味着只要出现实际的量子计算机,现有的以传统公钥密码为基石建立的安全系统将丧失所有的安全性。
- 效率挑战:传统公钥密码算法的密钥长度一直在增加,使得传统密码算法码效率很低。通过寻找具有更简单运算的数学难题,来降低加解密操作的复杂性,有代表性的是基于格的密码系统,其基本运算为矢量的加法和乘法。和RSA相比,椭圆曲线算法尽管密钥和密文较短,但在椭圆曲线加法群上所进行的操作还是十分复杂,效率改善不大。
格问题
格的困难问题:格问题的主要形式是寻找满足某种最小化特性的格矢量,最为经典的格问题是最短矢量问题(SVP)和最近矢量问题(CVP) 。SVP、 CVP、最短线性无关向量问题(SIVP)和最短基问题(SBP)问题都是直接的格问题,而其他问题则是与格问题密切相关的问题,如有限距离解码问题(BDD)可形式化为最近矢量问题(CVP)的特例,通过选择合适的误差参数,有误差学习问题(LWE)又可看作是特定格上的 CVP 问题,也可转换后描述为 BDD 问题。
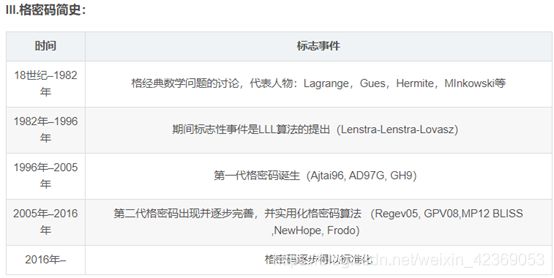
格密码发展
主要历史简述:
- 19世纪早期,主要从数学角度研究格,基本未考虑其应用意义
- 1801年从高斯开始,Hermite(1850)、Minkowski(1896)对推动格的研究贡献巨大
- 往后,LLL算法——主要用于求格中的近似最短向量以及实数域上分解多项式
格密码特点
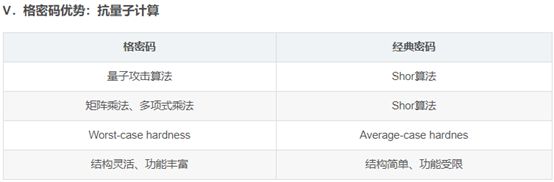
优势:基于格的密码系统是后量子计算时代的密码候选方案之一,其优势如下:
- 抗量子攻击:这是格密码相对于传统的公钥密码学最主要的优势,传统的公钥密码学在量子计算机的环境下安全性是没有保证的。传统的公钥密码系统大部分都是以大整数分解以及离散对数问题作为底层的安全性保证的(密码学的本质实质上是利用一个数学上可证明非常困难的问题来达到安全的目的)。目前还不存在解决某些格困难问题的多项式量子算法,因此,基于格难题所设计的新型公钥密码体质可以抵御量子攻击。Shor在1997年给出了一种可以有效解决这些问题的量子算法(以前被认为是非常困难的问题,现在变得不那么困难了)。所以,因为能够可以有效抵抗量子攻击,格理论密码系统在近些年成为了研究的热门。
- 算法效率高,高并行性:格密码系统中主要是向量之间的运算,不涉及大质数等大数的运算,且算法的并行度相对较高。所以,格密码系统中算法的效率相对较高(但现有的格密码系统中都存在密钥长度较大的问题,这是格密码系统应用的主要困难之一)。
- 由于格是一种线性结构,格上的运算大多是线性运算,因此利用格难题所构建的新型公钥密码体质比现有方案运算速度更快;
- 强安全性保障:Ajtai给出了一项证明,只要一些相关的格问题在最坏情况下是困难的,就能证明某些问题在平均情况下是困难的。由于格的最短矢量问题(SVP)和格的最近矢量问题(CVP)被证明在随机归约下均属于NP-hard类问题。即某一类格中一些问题的平均难度等价于格上一类NP问题的难度。因此,在这些格问题基础上构建的公钥密码体制,其任意一个实例的安全性与其最难实例的安全性相同;
- 在格理论密码系统出现之前,没有合适的问题可以用于构造同态加密系统。
LLL算法
LLL算法——以格规约(lattice)基数为输入,输出短正交向量基数。
LWE(Learning With Errors)
2005 年, Regev 提出了带错误的学习问题 (LWE), 证明了 LWE 与格上困难问题 (如近似最短向量问题 Gap-SVP) 相关, 并给出了基于 LWE 的公钥密码方案。与之前出现的格上困难问题比较, LWE 在构建密码系统时更方便。LWE算法与最坏情况下的格问题一样难,而最坏情况下的格问题被认为是指数级难(即使面对的是量子计算机)。
注:仅作资料整理!
如有错误、侵权,请联系笔者更改、删除!!!